【微积分下】3.26第一次小组讨论

8.2,8.3小组讨论问题总结

7.请你解释一下二元函数\(f(x,y)\)在\((x_0,y_0)\)点处全微分概念的数学本质。

在一元函数中，\(y\)的微分为\(dy=f'(x)dx\),参照一元函数微分的本质\(dy\)是棍鱼\(dx\)对应的切线增量（\(dx\)是关于\(a\)点的横向增量）

微分，二维上本质上是对改变量\(\Delta y\)的近似，即\(\Delta y=f'(x)dx+o(x)\)其中\(f'(x)dx\)为线性主部，即\(dy\)。这是一种化曲为直来逼近的思想。

同样推广在三维曲面上，经过\(P(x_0,y_0)\)二维曲面有无数个切线，为了计算方便，取平行于\(xOz\)和\(yOz\)的平面与曲面产生的相交曲线，分别类似一元函数求微分，而这两条曲线在\(P(x_0,y_0)\)上的切线斜率，即为函数关于\(y和x\)的偏导数即\(f'_x(x_0,y_0),f'_y(x_0,y_0)\)

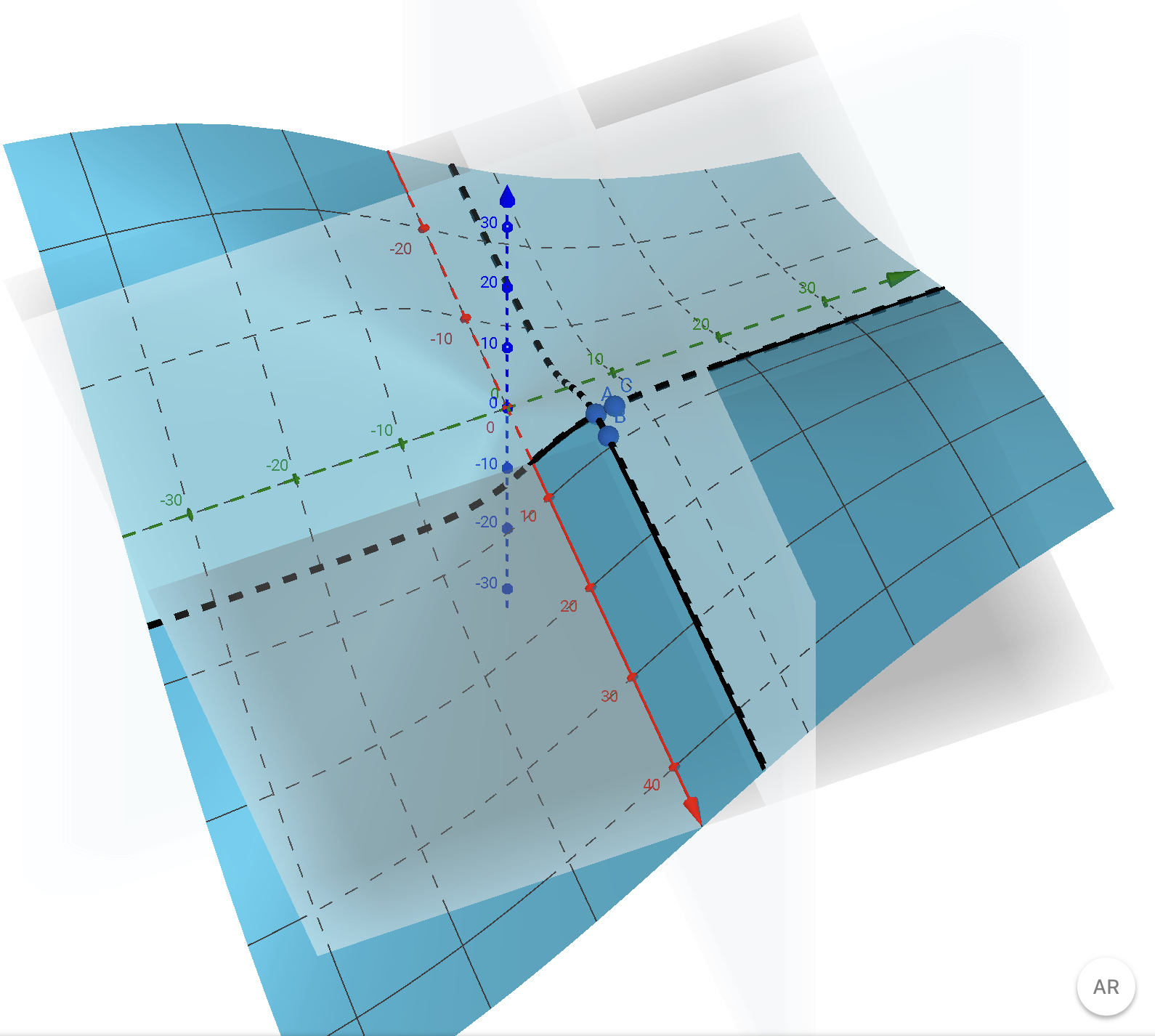
从直观的理解上，类似与爬坡，\(x,y\)的改变影响着\(z\)的改变，也就是说\(dz\)是由\(dx\)和\(dy\)共同决定的

\[dz=dx影响的改变量+dy影响的改变量 \]

从根本定义来看

\[\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y) \]

而这\(dx\)影响的改变量，一位平面上即为\(f'_x(x_0,y_0)dx+o(\Delta x)\)

\[即dz=f'_x(x_0,y_0)dx+o(\Delta x)+f'_y(x_0,y_0)dy+o(\Delta y) \]

\[dz=f'_x(x_0,y_0)dx+f'_y(x_0,y_0)dy+o(\rho) \]

其中\(\rho\)为\(\sqrt{(\Delta x)^2+(\Delta y)^2}\)即在\(P(x_0,y_0)\)为圆心，半径为\(\rho\)的微小球改变量，

二元微分，从二维拓展来看，是用一个平面来代替曲面，就用同在二维下用直线代替曲线

而两条曲线的切线形成一个平面即为此平面，用\(dx\)和\(dy\)在此曲面上的改变量来近似在整个三维曲面上的改变量。换做四维空间也同理

即全微分是通过各自变量的改变量对结果产生变化之和来近似结果的真是改变量

\[即dw=\frac{\partial w}{\partial x}dx+\frac{\partial w}{\partial y}dy+\frac{\partial w}{\partial z}dz+…… \]

8.如何计算二元函数的全微分？三元函数的全微分呢？总结\(n(n\ge2)\)元函数的全微分计算方法有哪些？

方法一

适用于初等函数或者分段函数非分段点

直接计算\(dw=\frac{\partial w}{\partial x}dx+\frac{\partial w}{\partial y}dy+\frac{\partial w}{\partial z}dz+……\)即可

方法二

**分段函数分段点 **

以二元函数为例，n元函数同理

• 首先求在\(P(x_0,y_0,z_0,……)\)处是否连续，连续则继续，不连续则不可微
• 计算偏导数\(f'_x(x_0,y_0,z_0,……),f'_y(x_0,y_0,z_0,……)\)，……若存在则继续，有一个不存在则不可微
• 计算\(\lim\limits_{\rho\to 0} \frac{\Delta w-（\frac{\partial w}{\partial x}dx+\frac{\partial w}{\partial y}dy+\frac{\partial w}{\partial z}dz+……）}{\rho}\),\(\rho=\sqrt{(\Delta x)^2+(\Delta y)^2}\)若极限为0(余项为\(\rho\)的高阶无穷小)时，可微，此时可以通过方法一直接计算，反之不可微

其中\(\Delta w\)有时可以通过\(\Delta w=f(x+\Delta x,y+\Delta y)-f(x,y)\)直接计算来减小运算量

9.请给出并分析二元函数\(f(x,y)\)在\((x_0,y_0)\)点处的可微性与可导性、连续性以及偏导数连续之间的关系。

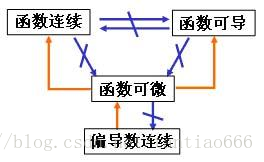
• 连续不一定可导，例如绝对值函数。

• 可导不一定连续：可导可能是指\(x\)轴可导，而二元函数中有两个变量，无法得出另外一个也可导

• 连续不一定可微：例如绝对值函数

• 可导不一定可微：多元函数可能有多个方向，可导不一定连续，不连续一定不可微

• 可微一定连续：

  \[$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)=A\Delta x+B\Delta y+o(\rho)$ \]

  先遗像得

  \[\Delta z=f(x+\Delta x,y+\Delta y)=f(x,y)+A\Delta x+B\Delta y+o(\rho) \]

  两侧取极限即

  \[\lim\limits_{\Delta x\to 0}f(x+\Delta x,y+\Delta y)=f(x,y) \]

  此为函数连续定义，即可证

• 偏导连续则函数可微

  切平面

• 函数可微偏导不一定连续

  例如

  \[f(x,y)=\left\{ \begin{array}{rcl} (x^2+y^2)sin\frac{1}{\sqrt{x^2+y^2}} x^2+y^2\ne 0\\ 0 & x^2+y^2= 0 \end{array} \right. \]

11.求函数\(f(x,y,z)=\sqrt[z]{\frac{x}y}\)在\((1,1,1)\)处的全微分为

\[df(x,y,z)=\frac{\partial }{\partial x}dx+\frac{\partial }{\partial y}dy+\frac{\partial }{\partial z}dz \]

\[\frac{\partial }{\partial x}=\sqrt[z]{\frac{x}y}\frac1{2x} \]

\[\frac{\partial }{\partial y}=-\sqrt[z]{\frac{x}y}\frac1{2y} \]

\[\frac{\partial }{\partial z}=\sqrt[z]{\frac{x}y}\frac1{z^2}ln\sqrt\frac{x}{y} \]

\[即df(x,y,z)=\sqrt[z]{\frac{x}y}（\frac1{2x}dx-\frac1{2y}dy+\frac1{z^2}ln\sqrt\frac{x}{y}dz） \]