【题解】P5522 [yLOI2019] 棠梨煎雪

题目描述

扶苏是一个非常喜欢边听古风鸽边写数学题的人，因此这道题其实是个五三原题。

扶苏希望重现青原上樱花盛开的景色，于是他准备了很多互不相同樱花树幼苗，准备种成一行。

这一行中，一共有 n 个位置可以种下樱花，而扶苏准备了 m 支幼苗。由于樱花盛放时对左右空间需求非常大，所以樱花不能紧挨着种植，也就是任意两支幼苗之间必须至少存在一个不种花的空位置。

按照这种方式种花并不难，但是令扶苏感到好奇的是一共有多少合法的方案让他把这 m 支幼苗都种下去。一个方案是合法的当且仅当他满足上一段中叙述的要求。如果我们将花按照 1, 2, 3 … m 编号，两种方案不同当且仅当被选择种花的位置不同或从左向右数花的编号序列不同。

为了避免输出过大，答案对一个参数 p 取模。

输入格式

每个输入文件中有且仅有一组测试数据。

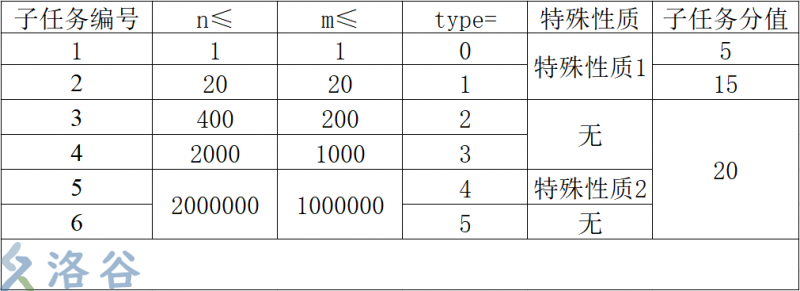
测试数据只有一行四个数字，依次代表type, n, m, p，其中 type 是一个帮助你判断测试点类型的参数，会在数据范围中说明。

输出格式

输出一行一个数字，代表答案对 p 取模的结果。

输入 #1

1 3 2 19260718

输出 #1

2

大意就是将\(n\)个球放到\(m\)个盒子里，且球之间至少隔一个盒子，直接上手组合就完事了
每一个树都是有编号的，所以我们不是很好直接排列组合
一种思路是假设这一堆树都是一样的，最后结果再乘上\(m!\)个树的排列，就是最后的结果
下面就是排树了，记得之前考试曾经做过一个这样的数学题，滑雪登山还是啥的忘了，也是隔一格以上放一个，那个比较少，直接分情况讨论是可以做的，但这又不是数学题。
我们反过来想，我们把树定下，排列空位。首先是定下\(m\)棵树，我们有\(n-m\)个空位子，首先先把树之间的都填一个，要填掉\(m-1\)个空位，所以还剩下\(n-2m+1\)个空位子
我们就要考虑剩下的几个空位子要怎么放了，因为我们已经排好了空位子了，所以这些空位子怎么填也就无所谓了，我们只需要把它们分到树之间或者首末就好了，也就是说我们需要把\(n-2m+1\)个空位分到\(m+1\)组中去。
利用高中数学所学到的隔板法来分，把\(n-2m+1\)个球分到\(m+1\)个盒子中，可以有空盒。
所以我们得到了方法数为

\[C^m_{(n-2m+1)+m}=C^m_{n-m+1} \]

最后相乘就好了。这是初始代码

#include<cstdio>
int c[10002][10002];
int mo;
long long ans1=1,ans2;
void pascal()//用来求组合数的帕斯卡三角形
{
    c[0][0]=c[1][0]=1;
    for(int i=1;i<=10000;i++)
        for(int j=0;j<=i;j++)
        {
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%mo;
        }
    return;
}
int main()
{
    int type,n,m;
    scanf("%d%d%d%d",&type,&n,&m,&mo);
    pascal();
    for(int i=1;i<=m;i++)ans1=(ans1*i)%mo;
    ans2=c[n-m+1][m];
    printf("%lld",(ans1*ans2)%mo);
    return 0;
}

作为一个屁事不管的二货，自然是看不到了，从数据范围来看的话\(100000^2\)的二维数组是肯定要炸的，小了数据不通过。
漏了一个点，在前面的排列中，我们乘了一个\(m!\),然后在最后的空位组合中我们又除了一个\(m!\)（在帕斯卡三角形中完成的），那不就相当于排列了么，所以方法数为

\[A^m_{n-m+1} \]

更改后的代码

#include<cstdio>
long long mo,ans=1;
int main()
{
    int type,n,m;
    scanf("%d%d%d%lld",&type,&n,&m,&mo);
    for(int i=n-m+1;i>n-2*m+1;i--)ans=ans*i%mo;
    printf("%lld",ans%mo);
    return 0;
}