GAN主要公式推导

GAN公式的主要推导

论文概述

由Ian Goodfellow等人于2014年发表的里程碑式论文《Generative Adversarial Nets》提出了生成对抗网络(GAN)这一革命性的深度学习框架。论文通过对抗过程来估计生成模型，同时训练两个模型：生成模型G(捕捉数据分布)和判别模型D(估计样本来自训练数据而非G的概率)。

核心思想

通俗点来说，类似于生活中"左右互博"
GAN框架包括了两个相互对抗的神经网络：

• 生成器（Generator,G）：用于生成伪造的数据样本；
• 判别器（Discriminator,D）：用于区分生成数据与真实数据，可以理解为一个二分类任务。
  两者通过一个叫做minmax game的策略进行训练

补充：Minmax play:

• 极大极小博弈，属于博弈论中的经典概念，尤其用于零和博弈（即一方的得益等于另一方的损失）。
  核心思想为：
  • 最大化自身的的最小收益
  • 最小化对方的最大收益

假设有payoff矩阵M，行方为玩家A的策略集合，列方为玩家B的策略集合，则对于双方分别有：
A的Minmax值为：

\[max_{x \in X}min_{y \in Y}M(x,y) \]

B的Minmax值为：

\[max_{y \in Y}min_{x \in X}M(x,y) \]

当两者相等时，我们称之为Minmax平衡，即所谓的Nash均衡在零和博弈中的特例。

• 训练步骤
  

1. 超参数k（关键设计）：

   • 控制判别器/生成器的更新比例，原论文中生成器的训练次数固定为1，所以k直接与判别器的训练次数成正比例
   • 原始论文采用k=1（判别器1步 vs 生成器1步）
   • 理论依据：判别器需要更频繁更新以保持"接近最优"

2. 双采样机制：

   • 噪声采样：\(z^{(i)} \sim p_z(z)\) （通常为标准正态分布）
   • 数据采样：\(x^{(i)} \sim p_{data}(x)\) （训练数据集）
   • 小批量处理（m样本）是深度学习标准实践

3. 梯度更新公式：

   • 判别器梯度（最大化目标）：
     \[\nabla_{\theta_d}\frac{1}{m}\sum_{i=1}^m [\underbrace{\log D(x^{(i)})}_{\text{真实数据得分}} + \underbrace{\log(1-D(G(z^{(i)})))}_{\text{生成数据判别}}] \]

   • 生成器梯度（最小化目标）：
     \[\nabla_{\theta_g}\frac{1}{m}\sum_{i=1}^m \underbrace{\log(1-D(G(z^{(i)})))}_{\text{生成器欺骗目标}} \]

   • 原论文中采用了带有动量的SGD（随机梯度下降优化算法），现在常采用Adam优化算法。
   • 判断收敛的条件：生成样本的视觉质量趋于稳定，并且判别器无法持续提升准确率。

4. 过程图如下：
   

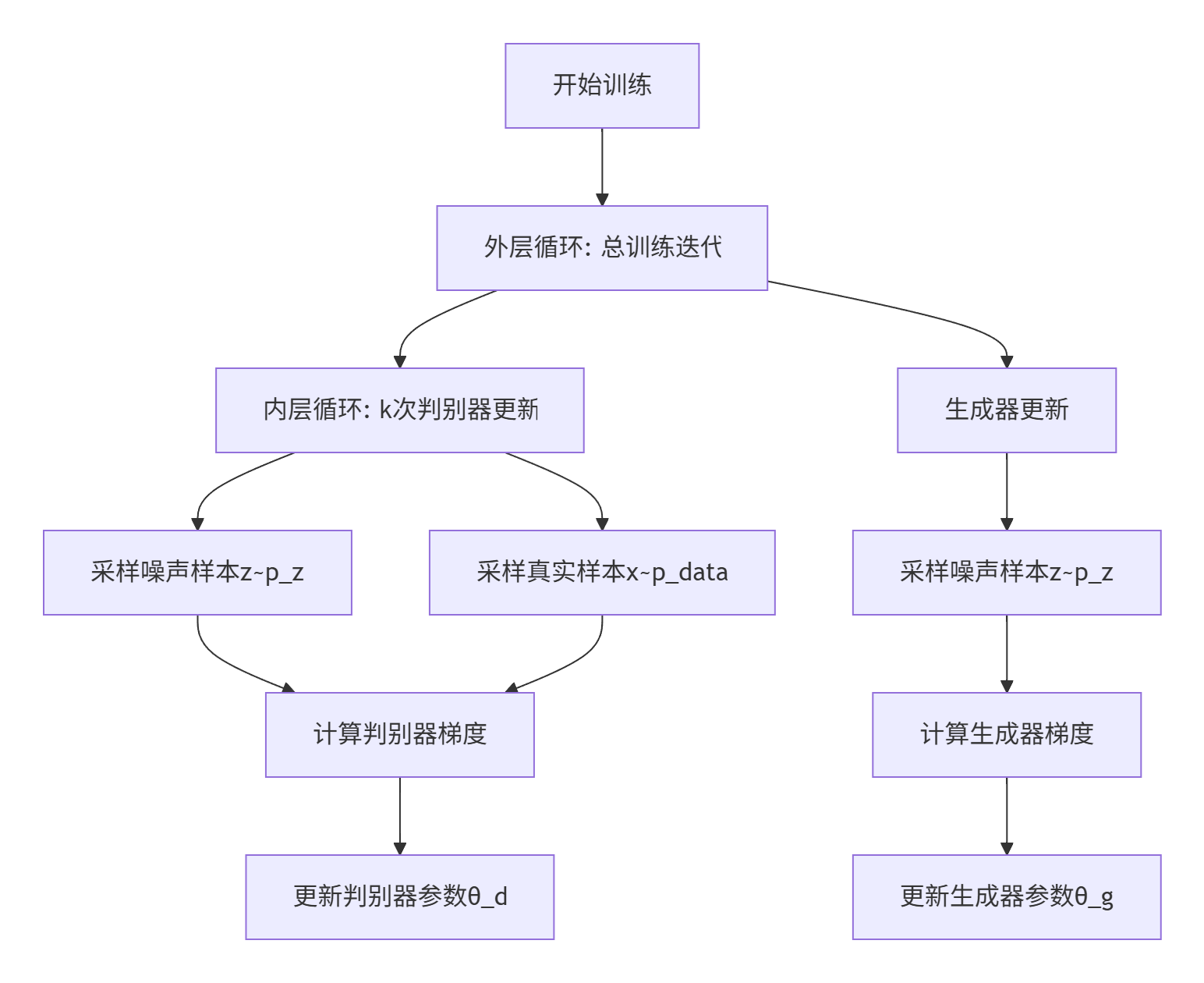
公式解读

page3.formula 1

\[\min_G\max_DV(D,G)=\mathbb{E}_{\boldsymbol{x}\sim p_{\boldsymbol{data}}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z}\sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log(1-D(G(\boldsymbol{z})))].\quad (1) \]

该公式表示为GAN中关于生成器和判别器训练过程中的Minmax策略

推导过程：

1. 判别器D的目标是最大化识别真实和生成样本的能力
2. 生成器的G的目标是最小化判别器的识别能力，转而言之，就是让生成的样本越接近真实样本越好，能够“骗过”判别器
3. x是服从于真实数据分布\(p_{data}\)的样本，z是服从于先验噪声分布\(p_z\)的样本（通常为高斯分布或者正态分布），注意z是噪声
4. 其中两个数学期望经过连续展开之后即可变换为：
   \[V(G,D)=\int_{x}p_{data}(x)\log D(x)dx+\int_{z}p_{z}(z)\log(1-D(G(z)))dz \]

这就是公式3中的第一步

本质上，GAN的目标是通过优化整个数据空间上的损失（概率分布的平均表现），而不是某个具体样本的损失，这样才能保证\(G\)和\(D\)真正学到整个分布的信息。这就是为什么min-max目标是一个数学期望。

page4.formula 2&3&4

\[D_G^*(\boldsymbol{x})=\frac{p_{data}(\boldsymbol{x})}{p_{data}(\boldsymbol{x})+p_g(\boldsymbol{x})}\quad(2) \]

该公式表示的是在给定生成器G的情况下，最佳的判别器可以用如上公式表述。

推导过程

通过函数关系\(G(z) = x\),故

\[\begin{aligned}V(G,D)&=\int_{\boldsymbol{x}}p_{\mathbf{data}}(\boldsymbol{x})\log(D(\boldsymbol{x}))dx+\int_{z}p_{\boldsymbol{z}}(\boldsymbol{z})\log(1-D(g(\boldsymbol{z})))dz\\&=\int_{\boldsymbol{x}}p_{\mathbf{data}}(\boldsymbol{x})\log(D(\boldsymbol{x}))+p_{g}(\boldsymbol{x})\log(1-D(\boldsymbol{x}))dx\quad(3)\end{aligned} \]

具体操作步骤：
采用概率密度变换公式是实现从噪声空间 z 到数据空间 x 转换。
基础数学原理：
概率密度变换公式描述了两个随机变量之间的密度函数关系：
给定随机变量 \( \(z \sim p_z(z)\) \) 和变换 \( \(x = G(z)\) \)，则 \( x \) 的密度函数为：

\[p_g(x) = p_z(z)\cdot \left| \det\left( \frac{\partial z}{\partial x} \right) \right| \]

对于确定性生成器 \( G \)（通常情况）：

• 若 \( G \) 可逆，直接应用变量替换：
  \[p_g(x) = p_z(G^{-1}(x)) \cdot \left| \det\left( \frac{\partial G^{-1}(x)}{\partial x} \right) \right| \]

• 若 \( G \) 不可逆（如维度变化），需引入隐式密度：
  \[p_g(x) = \int \delta(x - G(z)) p_z(z) dz \]

其中 \( \(\delta(\cdot)\)\) 是Dirac delta函数。
2. 推导过程：
2.1. 变量替换：
令 \( x = G(z) \)，则 \( \(z = G^{-1}(x)\) \)（假设 \( G \) 可逆）
2.2 概率密度变换：

\[dz = \left| \det\left( \frac{\partial G^{-1}(x)}{\partial x} \right) \right| dx \]

2.3. 积分转换：

\[\int_z p_z(z)\log(1-D(G(z)))dz = \int_x p_z(G^{-1}(x)) \left| \det\left( \frac{\partial G^{-1}(x)}{\partial x} \right) \right| \log(1-D(x))dx \]

2.4. 定义生成分布：
又因为根据隐式密度定义：

\[p_g(x) = p_z(G^{-1}(x)) \cdot \left| \det\left( \frac{\partial G^{-1}(x)}{\partial x} \right) \right| \]

2.5. 所以即可推导出：

\[\int_{z}p_{z}(z)\log(1-D(G(z)))dz = \int_x p_g(x)\log(1-D(x))dx \]

2.6 又公式3中的被积函数可以简写为：

\[p_{data}\log D+p_{g}\log(1-D) \]

2.7 对上述的被积函数进行求极值:

\[\frac{\partial}{\partial D}\left[p_{data}\log D+p_g\log(1-D)\right] \]

⭐Supplement：
为什么是对被积函数进行求极值而不是直接针对V（D）?
a. 变分法和积分极值之间的关系：

b. 答案：

2.8 求导得：

\[\frac{p_{data}}{D}-\frac{p_{g}}{1-D}=0 \]

2.9 解得，在G固定时，最有判别器可以表示为:

\[D_G^*(\boldsymbol{x})=\frac{p_{data}(\boldsymbol{x})}{p_{data}(\boldsymbol{x})+p_g(\boldsymbol{x})}\quad(2) \]

2.10 将公式2带入到公式3:\(V(G,D)=\int_{x}p_{data}(x)\log(D(x))+p_{g}(x)\log(1-D(x))dx\)可得：

\[\begin{aligned}C(G)&=\max_{D}V(G,D)\\&=\mathbb{E}_{x\sim p_{\mathrm{data}}}[\log D_{G}^{*}(x)]+\mathbb{E}_{z\sim p_{z}}[\log(1-D_{G}^{*}(G(\boldsymbol{z})))]&\quad{(4)}\\&=\mathbb{E}_{x\sim p_{\mathrm{data}}}[\log D_{G}^{*}(x)]+\mathbb{E}_{x\sim p_{g}}[\log(1-D_{G}^{*}(G(\boldsymbol{x}))]\\&=\mathbb{E}_{x\sim p_{\mathrm{data}}}\left[\log\frac{p_{\mathrm{data}}(x)}{P_{\mathrm{data}}(x)+p_{g}(x)}\right]+\mathbb{E}_{x\sim p_{g}}\left[\log\frac{p_{g}(x)}{p_{\mathrm{data}}(x)+p_{g}(x)}\right]\end{aligned} \]

⭐supplement（考研数学概率论与统计知识）:

page4.formula 5&6

\[C(G) = -\log(4) + KL\left(p_{\text{data}} \left\| \frac{p_{\text{data}} + p_g}{2} \right.\right) + KL\left(p_g \left\| \frac{p_{\text{data}} + p_g}{2} \right.\right) \quad(5)\]

推导过程

3.1 训练过程中实现了Nash平衡，此时对抗训练双方的处于最优稳定状态，此时\(P_{data}=P_{g}\),则\(D_{G}^*(x) = 0.5\)。

3.2 为了凑出JSD散度的表达形式，对于公式4中存在的\(log\frac{P_{data}}{P_{data}+P_{g}}\)和\(log\frac{P_{g}}{P_{data}+P_{g}}\)进行如下变换：

• \(\log\frac{p_{data}}{p_{data}+p_g}=\log\left(\frac{2p_{data}}{p_{data}+p_g}\right)-\log2\)
• \(\log\frac{p_g}{p_{data}+p_g}=\log\left(\frac{2p_g}{p_{data}+p_g}\right)-\log2\)

3.3 所以得到：

\[C(G)=\left(\mathbb{E}_{p_{data}}\left[\log\frac{2p_{data}}{p_{data}+p_{g}}\right]+\mathbb{E}_{p_{g}}\left[\log\frac{2p_{g}}{p_{data}+p_{g}}\right]\right)-2\log2 \]

3.4 根据KL离散度公式的定义，所以有

\[C(G)=-\log4+KL\left(p_{data}\left\|\frac{p_{data}+p_g}2\right)+KL\left(p_g\left\|\frac{p_{data}+p_g}2\right)\right.\right. \quad(5) \]

3.5 又根据JSD的定义，所以有

\[C(G)=-\log(4)+2\cdot JSD\left(p_\text{data}\|p_g\right)\quad(6) \]

⭐supplement：

1. Nash平衡存在性（博弈论）：
   Nash平衡又称为Nash均衡，是博弈论中的核心概念，描述了在非合作博弈中所有参与者策略的最优稳定状态，任何单方改变策略都无法获得额外收益。
   所以当且仅当\(p_g=p_{data}\)时，达到判别器与生成器对抗训练的平衡点。此时\(D^*_G(x)=0.5\),带入公式4可得

\[V(G,D)=-\log(4) \]

2. KL散度（测度论）：
   全称为Kullback-Leibler divergence,被作为衡量概率分布差异的基本工具
   
   数学表达式通常为：

\[\begin{aligned} KL(P \| Q) &= \int P(x) \log \left( \frac{P(x)}{Q(x)} \right) dx \\ &= \mathbb{E}_{x \sim P} \left[ \log \frac{P(x)}{Q(x)} \right] \end{aligned}\]

核心特性：

• 非对称性：\(D_{KL}(P\|Q)\neq D_{KL}(Q\|P)\)
• 非负性：\(D_{KL}\geq 0\),当且仅当\(P=Q\)时为0
• 信息论解释:表示\(Q\)近似\(P\)时的信息损失

3. JSD散度

• Jensen-Shannon散度（Jensen-Shannon Divergence, JSD）是KL散度的对称平滑版本
• 基础定义：
  对于两个概率分布\(P\)和\(Q\),JSD散度为：

\[JSD(P\|Q)=\frac12KL\left(P\left\|\frac{P+Q}2\right)+\frac12KL\left(Q\left\|\frac{P+Q}2\right)\right.\right. \]

其中\(M=\frac{P+Q}{2}\)称为中间分布。

• 将KL散度展开后得到：

\[JSD(P\|Q)=\frac{1}{2} \left[\int P(x)log\left(\frac{2P(x)}{P(x)+Q(x)}\right)dx+\int Q(x)log\left(\frac{2Q(x)}{P(x)+Q(x)}\right)dx\right] \]

• 数学期望表示为：

\[JSD(P\|Q)=\frac{1}{2}E_{x \sim P}\left[log\left(\frac{2P(x)}{P(x)+Q(x)}\right)\right]+\frac{1}{2}E_{x \sim Q}\left[log\left(\frac{2Q(x)}{P(x)+Q(x)}\right)\right] \]

性质	说明
对称性	\(JSD(P|Q)=JSD(Q|P)\)
有界性	\(0 \leq JSD(P|Q) \leq log(2)\)
与KL的关系	当\(P=Q\)时，\(JSD=0\);当\(P⊥Q\)时，\(JSD=log(2)\)

总结（优化版）

本文主要对GAN原始论文中公式 (1) 至 (6) 的推导过程进行了系统梳理和详细解析。通过引入博弈论中的极大极小原理，明确了生成器与判别器之间对抗机制的理论基础，揭示了GAN训练目标实质上是一个零和博弈问题。

在推导过程中，我们深入剖析了以下关键要点：

1. Minimax目标函数（公式1）体现了生成器试图“欺骗”判别器、而判别器试图识别真实样本的动态对抗过程。本质上，这一目标函数通过对期望损失的最小最大化，引导网络学习整个数据分布，而非仅优化单个样本。

2. 最优判别器的形式表达（公式2）通过对损失函数的导数求解，得出了在生成器固定时判别器的最优解，其表达式精确反映了数据分布与生成分布之间的比值关系，为后续理论分析奠定了基础。

3. 损失函数的重构（公式3–4）通过变量替换和概率密度变换，引入了生成样本的隐式概率分布，将对抗训练目标重新表述为真实分布与生成分布在整个数据空间上的加权对数差异。

4. JSD散度的引入（公式5–6）是GAN理论中的一大亮点。论文通过引导损失函数向Jensen-Shannon散度的形式转换，建立了生成模型训练与概率分布距离之间的直接联系。最终证明，在达到Nash平衡时，生成分布将逼近真实分布，判别器输出为常数0.5，此时GAN的损失函数达到理论下界 \(-\log(4)\)。

综上所述，GAN的理论构建融合了博弈论、概率论、信息论与最优化理论等多个数学分支，在方法论上具有极高的创新性与启发性。尽管这篇开创性论文发表于2014年，距今已有十余年，但其提出的对抗训练框架不仅奠定了生成模型的重要基石，也持续引领着深度学习研究的发展方向。随着WGAN、StyleGAN、Diffusion等后续工作的不断推进，GAN的核心思想仍在不断演进和拓展，展现出强大的生命力与广阔的应用前景。