的确,在实际项目开发过程中,很少用到算法,导致对算法不太感冒,总是一知半解。最近打算leetcode上刷算法题,但基础不好,感觉真的寸步难行,所以还得踏踏实实的从基础抓起。今天就彻底理解一下堆排序,没有谁比谁聪明,努力终究能见到回报。
一.堆
1.堆是什么?这里的堆, 是指二叉堆,可以理解成就是数组arr[n],如果数组满足arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2],称为大顶堆;反之arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2],称为小顶堆;如
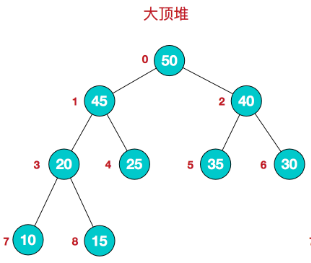
长度为8的数组A[50,45,40,20,25,35,30,10,15]就可以叫做一个大顶堆;上图中用二叉树表示,不过为方便理解,本质上就是一个数组而已。
同理,数组B[10,20,15,25,50,30,40,35,45]是一个小顶堆
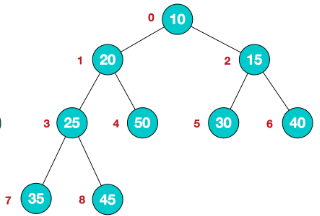
2.堆的特点,以长度为8的数组A大顶堆为例,下标0的值大于下标1和2的值,下标1的值大于下标3和下标4的值,下标2的值大于下标5和6的值.......数组中的第一个值总是最大的,或者说堆中的第一个值总是最大的,不知道大家有没有联想到定时任务?联想到优先队列?它们都是堆的应用场景
3.一个无序的数组怎样才能变成大顶堆?
我们以长度为15的数组C来说明,下图中的数字表示对应数组下标值
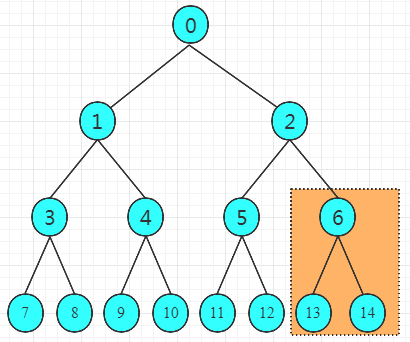
3.1)在下标为6、13、14这三个数的小结构中,要想实现大顶堆,怎么操作?很简单,下标13和14的值比较一下,找出大的,然后再和下标6的值比较一下,如果下标6的值小,交换一下,保证下标6所在的值大于下标13和14的值即可。同理下标5、11、12的小结构;4、9、10的小结构,3、7、8的小结构
3.2)依次进行比较交换,现在走到了2、5、6的这个小结构中,
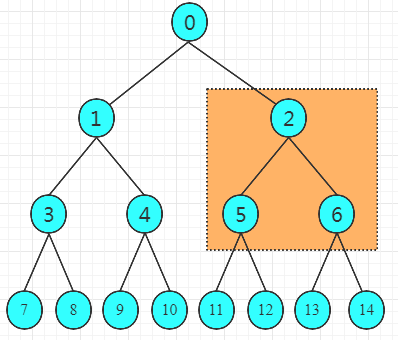
经过上面的步骤,此时下标5中的数值是大于下标11和12的,下标6中的数值是大于下标13和14的,如果下标2中的数值特别小,下标2要发生交换动作,和下标5、下标6中较大的数值交换,然后2、5、6这三个小结构满足大顶堆。然后,2、5、6是不是就结束了,开始进行下面的1、3、4和0、1、2?看个具体的例子【X,X,31,X,X,X,0,X,X,X,X,X,X,29,30】
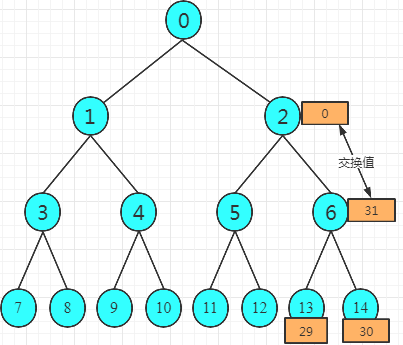
下标6的数值31被交换成了下标2的数值0以后,那下标13、14就要开始造反了,因为0没有29和30大呀,要重新比较下标6、13、14的这个小结构,小的值下沉,大的值上浮
......
就这样,比较下来,最终所有下标都要满足公式arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2],时间复杂度为O(logN).
理解过程,代码其实很简单了,数组到堆代码部分

1 public void arrayToHeap(int[] a) { 2 int len = a.length - 1;//长度为15的数组,最后一个下标是14 3 int beginIndex = (len - 1)/2;//从下标6开始,6、5、4、3、2、1、0 4 for (int i = beginIndex; i >= 0; i--) { 5 maxHeapify(a, i, len); 6 } 7 } 8 9 /** 10 * 小值下沉,大值上浮 11 * @param a 12 * @param curNode 13 * @param len 14 */ 15 private void maxHeapify(int[] a, int curNode, int len) { 16 int li = (curNode << 1) + 1; //下层左 6对应下层左13 17 if (li > len) return;//下层左 超出计算范围,直接返回 18 int ri = li + 1;//下层右 6对应下层右14 19 if (ri > len) return;//下层右 超出计算范围,直接返回 20 int cMax = li; 21 if (ri <= len && a[cMax] < a[ri]){//先判断左右,哪个较大 22 cMax = ri; 23 } 24 //如果下层左或右对应的值大于当前值,交换 25 if (a[cMax] > a[curNode]) {//大顶堆,若“<”表示小顶堆 26 swap(a, cMax, curNode);//对应数组值交换 27 maxHeapify(a, cMax, len);//交换后可能会导致下层的节点不符合大顶堆了,继续下层的可能交换动作 28 } 29 }
二.堆排序
1.数组C(0,n),满足大顶堆,数组中第一个数总是最大的,单独放好(交换到数组最后一个位置上);把C(0,n-1)再变成一个大顶堆,取出第一位最大值,放好(交换到数组倒数第二个位置上);把C(0,n-2)再变成一个大顶堆,取出第一位最大值,放好(交换到数组倒数第三个位置上)......最后数组从小到大排好顺序,时间复杂度O(NlogN),原地排序,空间复杂度O(1),堆排序不稳定(稳定性,是指在原序列中,arr[i]=arr[j],且arr[i]在arr[j]之前;排序后的序列中,arr[i]仍在arr[j]之前,则称这种排序算法是稳定的;否则称为不稳定的)
堆排序代码部分

1 public void heapSort(int[] a) { 2 //1.完整数组转堆 3 int len = a.length - 1;//长度为15的数组,最后一个下标是14 4 int beginIndex = (len - 1)/2;//从下标6开始,6、5、4、3、2、1、0 5 for (int i = beginIndex; i >= 0; i--) { 6 maxHeapify(a, i, len); 7 } 8 //2.交换堆中第一个值,剩下的数组再转成堆 9 for (int i = len; i > 0; i--) { 10 swap(a, 0, i);//每次取堆中第一位最大值交换堆中最后一位 11 maxHeapify(a,0, i - 1);//去掉第一位最大值后 再变成大顶堆 12 } 13 } 14 15 /** 16 * 小值下沉,大值上浮 17 * @param a 18 * @param curNode 19 * @param len 20 */ 21 private void maxHeapify(int[] a, int curNode, int len) { 22 int li = (curNode << 1) + 1; //下层左 6对应下层左13 23 if (li > len) return;//下层左 超出计算范围,直接返回 24 int ri = li + 1;//下层右 6对应下层右14 25 if (ri > len) return;//下层右 超出计算范围,直接返回 26 int cMax = li; 27 if (ri <= len && a[cMax] < a[ri]){//先判断左右,哪个较大 28 cMax = ri; 29 } 30 //如果下层左或右对应的值大于当前值,交换 31 if (a[cMax] > a[curNode]) {//大顶堆,若“<”表示小顶堆 32 swap(a, cMax, curNode);//对应数组值交换 33 maxHeapify(a, cMax, len);//交换后可能会导致下层的节点不符合大顶堆了,继续下层的可能交换动作 34 } 35 }






