本文和前一篇:动态规划5:两个字符串的最长公共子序列类似,但公共子串必须是连续的,子序列不需要连续
字符串a,长度为m:a[1].a[2].a[3].a[4]....a[m]
字符串b,长度为n:b[1].b[2].b[3].b[4]....b[n]
比如字符串a:abcbced;字符串b:acbcbcef则这两个字符串的最长公共子串长度为3,最长公共子串是:BCD,必须连续
1.一般的思路,双重for循环,操作字符串a,1)a在不在字符串b中,ab在不在字符串b中,abc在不在字符串b中,abcb在不在字符串b中,abcbc在不在字符串b中,abcbce在不在字符串b中,abcbcd在不在字符串b中;2)b在不在字符串b中,bc在不在字符串b中,bcb在不在字符串b中,bcbc在不在字符串b中,bcbce在不在字符串b中,bcbced在不在字符串b中......综上比较出一个最大值出来;缺点:时间复杂度高,双重for循环就m的平方了,String.contains()方法m*n;总的m立方*n
2.把两个字符串分别以行和列组成一个二维矩阵,比较二维矩阵中每个点对应行列字符中否相等,相等的话值设置为1,否则设置为0
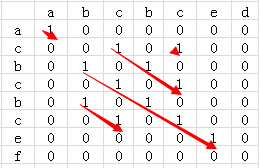
如果字符串a和字符串b完全一样,那二维矩阵正中间的对象线全是1,长度为字符串的长度。
如果字符串a和字符串b完全不一样,那二维矩阵中的值全是0,没有公共部分。
如果字符串a和字符串b不完全一样,怎么办呢?通过查找出值为1的最长对角线就能找到最长公共子串,也就是上图中的红色箭头,为什么是这样子的呢?再看一下上图想想就明白了
为了进一步优化算法的效率,在计算某个二维矩阵的值的时候顺便计算出来当前最长的公共子串的长度,即某个二维矩阵元素的值由dp[i][j]=1演变为dp[i][j]=1+dp[i-1][j-1],这样就避免了后续查找对角线长度的操作了。修改后的二维矩阵如下:
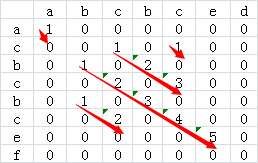
递推公式为:
当A[i] != B[j],dp[i][j] = 0
当A[i] == B[j],dp[i][j] = dp[i - 1][j - 1] + 1
同样,有初始值和递推方程,就可以求出最大长度值,进而求出对应子串
代码部分

1 public static void lcs(String x, String y) { 2 if(x==null||"".equals(x)||y==null||"".equals(y)){ 3 return; 4 } 5 int[][] dp = new int[x.length() + 1][y.length() + 1]; 6 int maxLength = 0; 7 int pos = 0; 8 for (int i = 0; i < x.length() + 1; i++) { 9 for (int j = 0; j < y.length() + 1; j++) { 10 if ((i == 0) || (j == 0)) { 11 dp[i][j] = 0; 12 } else if (x.charAt(i - 1) == y.charAt(j - 1)) { 13 dp[i][j] = dp[i - 1][j - 1] + 1; 14 if (dp[i][j] > maxLength) { 15 maxLength = dp[i][j]; 16 pos = i; 17 } 18 } 19 } 20 } 21 System.out.println("公共子串长度:"+maxLength); 22 System.out.println("公共子串:"+x.substring(pos-maxLength, pos)); 23 }





