一个机器人位于一个 m x n 网格的左上角,机器人每次只能向下或者向右移动一步,机器人试图达到网格的右下角
问总共有多少条不同的路径?
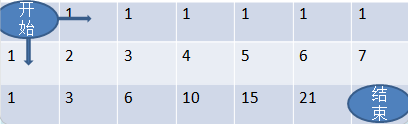
因为不能往上走,所以位于开始节点的第一层, 只能从左边一个格走到右边一格,可能的路径只能有1种;
因为不能往左走,所以位于开始节点的第一列, 只能从上边一个格走到下边一格,可能的路径只能有1种;
对于图中2所在的格子,可能是由上边一格走来的,也可能是由左边一格走来的,可能的路径=走到上边格的路径+走到左边格的可能;
对于图中左3所在的格子,可能是由上边2那一格走来的,也可能是由左边1那一格走来的,可能的路径=走到上边2格的路径+走到左边1格的可能;
对于图中右3所在的格子,可能是由上边1那一格走来的,也可能是由左边2那一格走来的,可能的路径=走到上边1格的路径+走到左边2格的可能;
...
从第一行第一列开始走到m行n列的可能路径=走到m行n-1列可能路径+走到m-1行n列路径,也即
dp[m][n]=dp[m][n-1]+dp[m-1][n];所以上图中,dp[3][7]=28,一共有28种可能性;
回到前一篇爬楼梯的问题,是不是很相似,爬楼梯只能往上走,这里是向右和向下,多了一个维度,所以数组也变成了二维




