单链表基础
单链表
为了避免顺序表结构的插入删除操作复杂,且元素个数受限等缺陷,引入了链式结构,在逻辑上还是顺序的,但在物理存储上不需要顺序存储,并且做到随用随分配内存,我们称这样的结构叫做链表。
创建一个单链表
typedef struct LNode {
ElemType data; //数据域
struct LNode *next; //指针域
}LNode, *LinkList;
头插法
采用头插法建立单链表,读入数据的顺序与生成的链表中的元素的顺序是相反的。每个结点的插入时间为\(O(1)\),设单链表长度为n,则总的时间复杂度为\(O(n)\)。
void CreatList1(LinkList &L, int n) { //头插法
LNode *p;
for(int i = 0; i < n; ++i) {
p = (LNode*)malloc(sizeof(LNode));
p->data = i;
p->next = L->next;
L->next = p;
}
}
尾插法
若希望读入数据和结点的次序一致,我们可以使用尾插法,此时必须增加一个q指针来记录尾结点。时间复杂度与头插法相同。
void CreatList2(LinkList &L, int n) { //尾插法
LNode *p, *q;
p = L;
for(int i = 0; i < n; ++i) {
q = (LNode*)malloc(sizeof(LNode));
q->data = i;
q->next = NULL;
p->next = q;
p = q;
}
}
循秩查找
即类似线性表,根据编号找到对应的元素。
LNode *GetEelm(LinkList L, int i) { //返回单链表第i个位置上结点(循秩查找)
int j = 1; //计数器,初始值为1
LNode *p = L->next;
if(i == 0) return L; //返回头结点
if(i < 0) return NULL; //不存在该节点
while(p && j < i) {
p = p->next;
j++;
}
return p;
}
按值查找
LNode *LocateElem(LinkList L, ElemType e) //按值查找结点
{
LNode *p = L->next;
while(p != NULL && p.data != e) p = p->next;
return p;
}
插入节点
首先检测要插入位置的合法性,然后找到要插入位置的前驱节点,然后调整结点域的指向即可。本算法的主要时间开销在寻找i的前驱节点,时间复杂度为\(O(n)\),若是在给定的结点后面插入新节点,则时间复杂度仅为\(O(1)\)。 一般是使用尾插的方法进行插入。
bool InsertLNode(LinkList &L, int i, Elemtype)
{
if(i <= 0) return false;
LNode *p = GetEelm(L, i - 1);
if(!p) return false;
LNode *q = (LNode*)malloc(sizeof(LNode));
q->next = p->next;
p->next = q;
return true;
}
扩展:前插操作
我们可以找到第i-2个结点,然后对其使用后插的方式插入即可。还有一种方法,是我们找到第i-1个结点,正常插入,然后交换数据域即可。
s->next = p->next;
p->next = s;
//交换数据域
temp = p->next;
p->data = s->data;
s->data = temp;
删除结点操作
首先检测要删除结点位置的合法性,然后找到要删除结点的前驱结点,再将要删除的结点删除即可。
和插入操作一样,本算法的主要耗时也是体现在查找前驱结点的过程中,时间复杂度为\(O(1)\)。
bool DeleteLNode(LinkList &L, int i, ElemType)
{
if(i <= 0) return false;
LNode *p = GetEelm(L, i - 1);
if(!p) return false;
LNode *q = p->next;
p->next = q->next;
free(q);
return true;
}
求单链表表长
求表长的操作就是计算单链表中数据结点(不含头结点的个数),需要从第一个结点开始顺序依次访问表中的每一个结点。算法的时间复杂度为
\(O(n)\)。
int LinkListLength(LinkList L)
{
int cnt = 0;
LNode *p = L->next;
while(p){
cnt++;
p = p->next;
}
return cnt;
}
单链表的逆置
单链表的逆置分为两种方法:头插法和就地逆置法,这两种方法虽然都能够达到逆置的效果,但这两种方法有很大的差别。
头插法
算法思路:依次取原链表中的每一个节点,将其作为第一个节点插入到新链表中,指针用来指向当前节点,p为空时结束。
void reverse1(LinkList &L)
{
LNode *p, *q;
*p = L->next;
L->next = NULL;
while(p) {
q = p;
p = p->next;
p->next = L->next;
L->next = p;
}
}
就地逆置法
分为迭代法和递归法。我们知道迭代是从前往后依次处理,直到循环到链尾;而递归恰恰相反,首先一直迭代到链尾也就是递归基判断的准则,然后再逐层返回处理到开头。总结来说,链表翻转操作的顺序对于迭代来说是从链头往链尾,而对于递归是从链尾往链头。
(1)非递归法:
下面是一个长度为5的单链表:
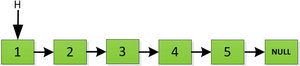
首先对于链表设置两个指针:
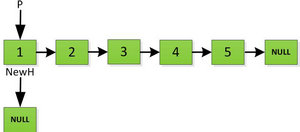
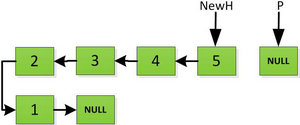
然后依次将旧链表上每一项添加在新链表的后面,然后新链表的头指针NewH移向新的链表头,如下图所示。此处需要注意,不可以上来立即将上图中P->next直接指向NewH,这样存放2的地址就会被丢弃,后续链表保存的数据也随之无法访问。而是应该设置一个临时指针tmp,先暂时指向P->next指向的地址空间,保存原链表后续数据。然后再让P->next指向NewH,最后P=tmp就可以取回原链表的数据了,所有循环访问也可以继续展开下去。
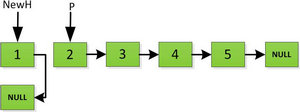
指针继续向后移动,直到P指针指向NULL停止迭代。
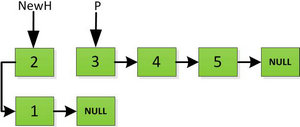
最后一步:
void reverse1(LinkList &L) //传入头结点的写法
{
LNode *p, *q;
p = L->next;
L->next = NULL;
while(p) {
q = p;
p = p->next;
q->next = L->next;
L->next = q;
}
}
(2)递归法:
我们再来看看递归实现链表翻转的实现,前面非递归方式是从前面数1开始往后依次处理,而递归方式则恰恰相反,它先循环找到最后面指向的数5,然后从5开始处理依次翻转整个链表。
首先指针H迭代到底如下图所示,并且设置一个新的指针作为翻转后的链表的头。由于整个链表翻转之后的头就是最后一个数,所以整个过程NewH指针一直指向存放5的地址空间。
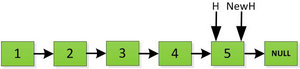
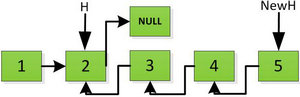
然后H指针逐层返回的时候依次做下图的处理,将H指向的地址赋值给H->next->next指针,并且一定要记得让H->next=NULL,也就是断开现在指针的链接,否则新的链表形成了环,下一层H->next->next赋值的时候会覆盖后续的值。
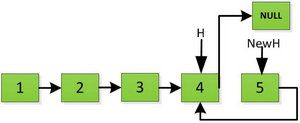
继续返回操作:
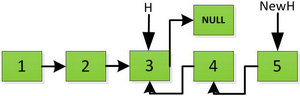
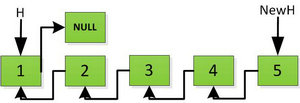
上图第一次如果没有将存放4空间的next指针赋值指向NULL,第二次H->next->next=H,就会将存放5的地址空间覆盖为3,这样链表一切都大乱了。接着逐层返回下去,直到对存放1的地址空间处理。
返回到头:
LNode *reverse2(LinkList &head) //传入头指针的写法
{
if(!head || !(head->next)) return head;
LNode * first = reverse2(head->next);
head->next->next = head;
head->next = NULL;
return first; //返回第一个节点的指针
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号