SUSTechCPC-2021Invitation Solution
SUSTechCPC-2021Invitation Solution
Problem A Satori Loves MP3
给出\(n(1\leq n \leq 10^3)\),数组\(t_i(1\leq i,t_i \leq n)\)。
若当前播放的歌为\(x\),下一首播放的歌则为\(t_x\)。
对于每一个\(i\),输出一行,初始播放歌\(i\)后最多能播放歌的种类数\(num_i\)。
本题在比赛中作为签到题存在。
对于每一个\(i\),找最大一个置换,这样的置换长度最多为\(n\),
所以显然有一个\(O(n^2)\)的暴力做法,对于\(1 \leq n\leq 10^3\)足以通过。
# include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int a[N];
bool vis[N];
int n;
int main() {
int n; scanf("%d",&n);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
for (int i=1;i<=n;i++) {
for (int j=1;j<=n;j++) vis[j]=false;
int cnt = 0,u = i;
while (!vis[u]) {
cnt++;
vis[u]=1;
u = a[u];
}
printf("%d\n",cnt);
}
return 0;
}
Problem B Game
给出\(n,m,p\ (1\leq n\leq 2\times 10^4,1\leq p \leq m \leq 60,1\leq p\leq 15)\),
给出\(n\)个长度为\(m\)的\(01\)字符串,保证这些字符串中\(1\)的个数小于等于\(p\)
从其中任意选择至少\(\lceil \frac{n}{2} \rceil\)个字符串,使得这些\(01\)字符串按位与,得到结果字符串\(t\)
最大化字符串\(t\)中\(1\)的个数。
由于按位与"有\(0\)变\(0\)"的性质,选择最少的字符串最后得到的答案一定比选择更多字符串得到答案更优。
随机选取一个字符串\(w\),它有\(\frac{1}{2}\)的概率在最终的答案中的 \(\lceil \frac{n}{2} \rceil\) 字符串中出现。
基于这个随机选取的字符串\(w\),我们尝试再找若干个和它"按位与"以后得到字符串至少含有一个\(1\)。
设这些字符串的集合为\(S\),若想最终的答案集合是\(S\)的子集和\(w\)的并集,那么就要让\(|S| \geq \lceil \frac{n}{2} \rceil -1\)。
现在问题就变成已知一些由集合组成的集合\(S\)(用\(01\)状态表示),对于一个集合\(mask\)来说有多少个集合\(T\in S\),让\(mask\)是\(T\)的子集。
设对于一个集合\(mask\)这个数量为\(cnt[mask]\),那么最后答案为所有\(cnt[mask]\geq \lceil \frac{n}{2} \rceil\)的\(mask\)中含有\(1\)个数最多的。
这可以用一个\(DP\)来完成,初始时只有已知的若干集合(用\(01\)状态表示)\(S\),将\(cnt[S] = 1\)
第一维循环枚举第\(i\)个元素,第二维循环从\(0\)开始往后遍历,始终保证对于当前位,当前\(cnt[mask]\)已经更新。用当前的更新值去更新\(mask|(1<<i)\)这个元素。
当然,由于选取的字符串只有\(\frac{1}{2}\)的概率在最终的答案集合中,所以上述操作还需要进行若干次保证得到正确答案的概率尽可能大。
经过上述算法\(x\),那么算法错误的概率为\(1-(\frac{1}{2})^x\),一般取\(x = 30\),可以保证错误概率很低。
时间复杂度\(O(x(nm+p\times 2^p))\)
# include <bits/stdc++.h>
using namespace std;
const int N=2e4+5;
const int M=65;
int n,m,p,a[N][M],back[M];
int cnt[1<<16];
int main()
{
srand(time(NULL)*10007);
int n,m,p; scanf("%d%d%d",&n,&m,&p);
for (int i=1;i<=n;i++) {
string s; cin>>s;
for (int j=0;j<m;j++)
a[i][j+1]=s[j]-'0';
}
int ans = 0;
for (int time=1;time<=30;time++) {
for (int i=0;i<(1<<15);i++) cnt[i]=0;
int r=1ll*rand()*rand()%n+1,cct = 0;
for (int i=1;i<=m;i++) back[i]=-1;
for (int i=1;i<=m;i++) if (a[r][i]) {
back[i]=cct++;
}
for (int i=1;i<=n;i++) {
int mask=0;
for (int j=1;j<=m;j++) if (back[j]!=-1&&a[i][j]) {
mask|=(1<<back[j]);
}
cnt[mask]++;
}
for (int i=0;i<15;i++)
for (int j=0;j<(1<<15);j++) if ((j>>i)&1) {
cnt[j^(1<<i)]+=cnt[j];
}
for (int i=0;i<(1<<15);i++) if (cnt[i]>=(1+n)/2) {
int res=0;
for (int j=0;j<15;j++) if ((i>>j)&1) res++;
ans=max(ans,res);
}
}
printf("%d\n",ans);
return 0;
}
Problem C Path
给出一个\(n\)个点\(m\)条边的有向图,以\((u,v,w)\)的方式给出边。
求从\(1\)为起点开始到其他各点的单元最短路径,路径的长度定义为这条路径上所有边权的乘积。
由于输出的数据太大,你只需要输出最短路径对\(998244353\)求余数的值即可。
\(1 \leq n,m \leq 2\times 10^5 , 1 \leq w \leq 998244353\)
如果是单元最短路的话,只需要进行一次\(dijkstra\)算法即可,但是这里定义的路径长度是边权乘积。
不好直接采用最短路算法,因为最短路径的长度太大,long long 存不下。
也不能采用对最短路求余数,显然这样并不满足三角条件,无法用\(dijkstra\)算法。
考虑转化,对边权取对数,那么乘积就转化为加和了,这样就可以用\(dijkstra\)算法了、
在跑实数的加和最短路的同时,记录一个\(ans[u]\)表示到达当前位置最短路对\(998244353\)求余的值。
时间复杂度\(O((n+m)log_2 n)\)
# include <bits/stdc++.h>
# define int long long
# define inf (1e18)
using namespace std;
const int N=2e5+10;
const int mo=998244353;
priority_queue< pair<double,int> >q;
bool v[N];
double d[N];
int tot,n,m;
int pre[N],ans[N],head[N];
struct Edge{
double w;
int pre,to,x;
}a[N<<1];
bool vis[N];
inline int read()
{
int X=0,w=0; char c=0;
while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar();
while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar();
return w?-X:X;
}
void adde(int u,int v,double w,int x) {
a[++tot].pre=head[u];
a[tot].to=v;
a[tot].w=w;
a[tot].x=x;
head[u]=tot;
}
void dijkstra() {
d[1]=0.0; ans[1]=1;
for (int i=2;i<=n;i++) d[i]=inf;
memset(v,0,sizeof(v));
q.push(make_pair(0.0,1));
while (q.size()) {
int u = q.top().second; q.pop();
if (v[u]) continue;
v[u]=1;
for (int i=head[u];i;i=a[i].pre) {
int v=a[i].to; double w = a[i].w; int x=a[i].x;
if (d[v]>d[u]+w) {
d[v]=d[u]+w;
ans[v]=ans[u]*x%mo;
q.push(make_pair(-d[v],v));
}
}
}
}
signed main() {
n=read();m=read();
for (int i=1;i<=m;i++) {
int u=read(),v=read(),x=read();
double w = log(x);
adde(u,v,w,x);
}
dijkstra();
for (int i=2;i<=n;i++) printf("%lld\n",ans[i]);
return 0;
}
Problem D Dating
给出\(n(1\leq n \leq 2\times 10^5)\)
求出一个长度为\(n\)的\(1-n\)的排列\(a_i\)
让\(b_i=|a_i-i|\)是长度为\(n\)的\(0-(n-1)\)的排列。
首先考虑到\(x\)取绝对值后\(|x|\)的奇偶性不变。
于是\(\sum\limits_{i=1}^{n} (a_i-i)\)的奇偶性和\(\sum\limits_{i=1}^{n}|a_i-i|\)的奇偶性相同。
由于\(\sum\limits_{i=1}^{n}(a_i-i)=\sum\limits_{i=1}^{n}a_i - \sum\limits_{i=1}^{n}i = 0\)为偶数,所以\(\sum\limits_{i=1}^{n}|a_i-i|\)也为偶数,即\(\sum\limits_{i=1}^{n}b_i = \frac{n(n-1)}{2}\)为偶数。
也就说\(n=4k\)或者\(n = 4k+1\),其中\(k\in N\)
下面进行构造,先考虑\(n=4k,k\in N\)的情况。
考虑构造一个有向图,边数和点数都为\(n\),要求边权是\(0-(n-1)\)的一个排列。
若一条边是由\(u\)指向\(v\)的,那么这条边的边权就是\(|u-v|\)。
先考虑一个比较显然的构造
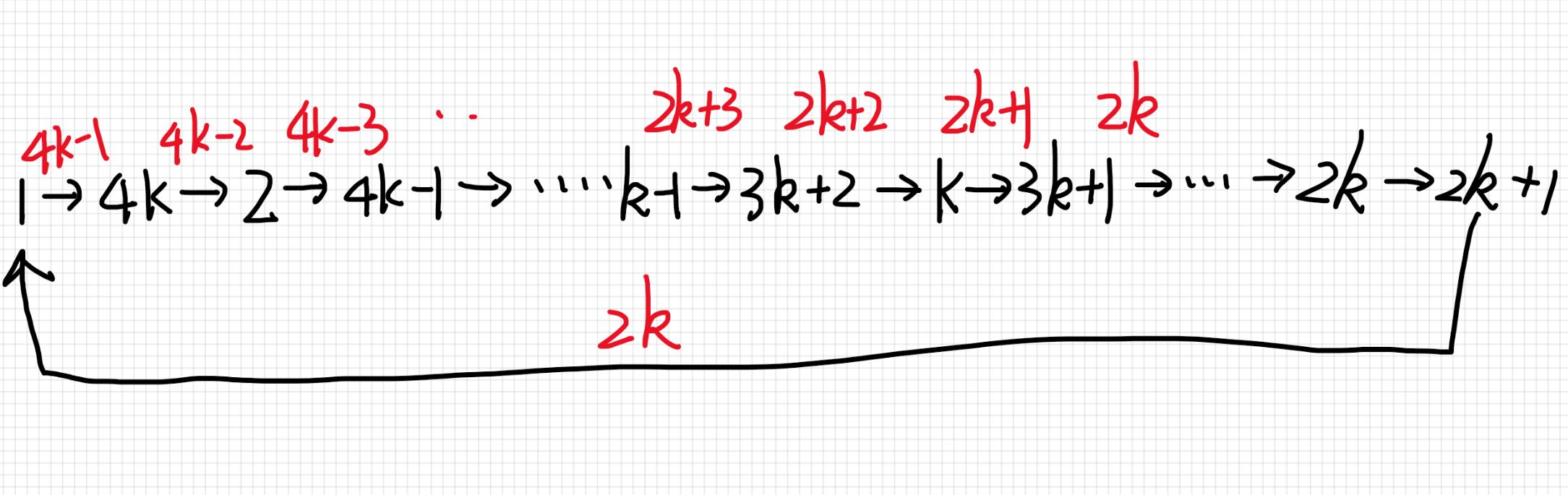
显然边权少一个\(0\),重复了一个\(2k\),在上述基础上对后半部分相邻两个交换,就变成:

相似的,构造\(n = 4k + 1\)的情况

规律是:
- 当 \(n \ne 4k \ and \ n \ne 4k+1\) 输出 “No More Dating ”
- 当 \(n= 4k \ or \ n =4k+1\) 从正中间开始向右两两交换,最右边的那个自成一个环,其他成为一个大环。
时间复杂度\(O(n)\)
# include <bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int a[N],ans[N];
int main() {
int n; scanf("%d",&n);
if (n%4==0||n%4==1) {
for (int i=0,l=1,r=n;i<n;i++)
a[i+1]=i&1?r--:l++;
for (int i=(1+n)/2+1;i<=n;i+=2) swap(a[i],a[i+1]);
for (int i=1;i<n-1;i++) ans[a[i]]=a[i+1];
ans[a[n-1]]=a[1],ans[a[n]]=a[n];
for (int i=1;i<=n;i++) printf("%d ",ans[i]);
} else puts("No More Dating");
return 0;
}
Problem E Sudoku
判断一个\(9\times 9\)的已经填好的数独是否符合:
- 每行是一个\(1-9\)的排列
- 每列是一个\(1-9\)的排列
- \(9\)个的\(3\times 3\)九宫格内分别是一个\(1-9\)的排列
如果符合,输出\(YES\),否则输出\(NO\)
直接模拟即可。
可以写一个\(pd(xl,xr,yl,yr)\)判断一个\((xl,yl)\)到\((yl,yr)\)矩形内是否是一个\(1-9\)的排列
来简化计算
时间复杂度:\(O(9\times 9)\)
# include <bits/stdc++.h>
using namespace std;
int a[10][10];
bool c[10];
bool pd(int xl,int xr,int yl,int yr) {
memset(c,false,sizeof(c));
for (int i=xl;i<=xr;i++)
for (int j=yl;j<=yr;j++) {
if (c[a[i][j]]) return false;
c[a[i][j]]=1;
}
return true;
}
bool check() {
for (int i=1;i<=9;i++) {
if (!pd(i,i,1,9)) return false;
if (!pd(1,9,i,i)) return false;
}
for (int i=1;i<=9;i+=3)
for (int j=1;j<=9;j+=3) {
if (!pd(i,i+2,j,j+2)) return false;
}
return true;
}
int main()
{
for (int i=1;i<=9;i++)
for (int j=1;j<=9;j++)
scanf("%d",&a[i][j]);
puts(check()?"YES":"NO");
return 0;
}
Problem F Flipped
- 网络流完全不会,带修改的网络流更加不会了
- skiped
- flipped
Problem G Meeting
有\(T (1 \leq T \leq 50000)\)组数据,每组数据给出四个坐标\((x_i,y_i) (1 \leq i\leq 4) , 0 \leq |x_i|,|y_i| \leq 10^8\)
定义两点\((x_1,y_1)\)和\((x_2,y_2)\)曼哈顿距离\(d = |x_1 - x_2|+|y_1-y_2|\)
在坐标系中选取一点\(P(x_0,y_0)\)让给出的四个点到\(P\)的曼哈顿距离的最大值最小。
对于每组数据,输出这个值。
考虑到对于一个点\((x,y)\)能够在\(l\)的曼哈顿距离走到的点是\((x',y')\),其中\(|x-x'|+|y-y'|\leq l\)
可以发现\((x',y')\)构成的集合图形是一个正方形,其边和\(y = x\)或\(y=-x\)分别平行。
接下来的问题就是判断四个正方形是否有交,那么将坐标系倾倒\(45°\)将正方形摆正即可。
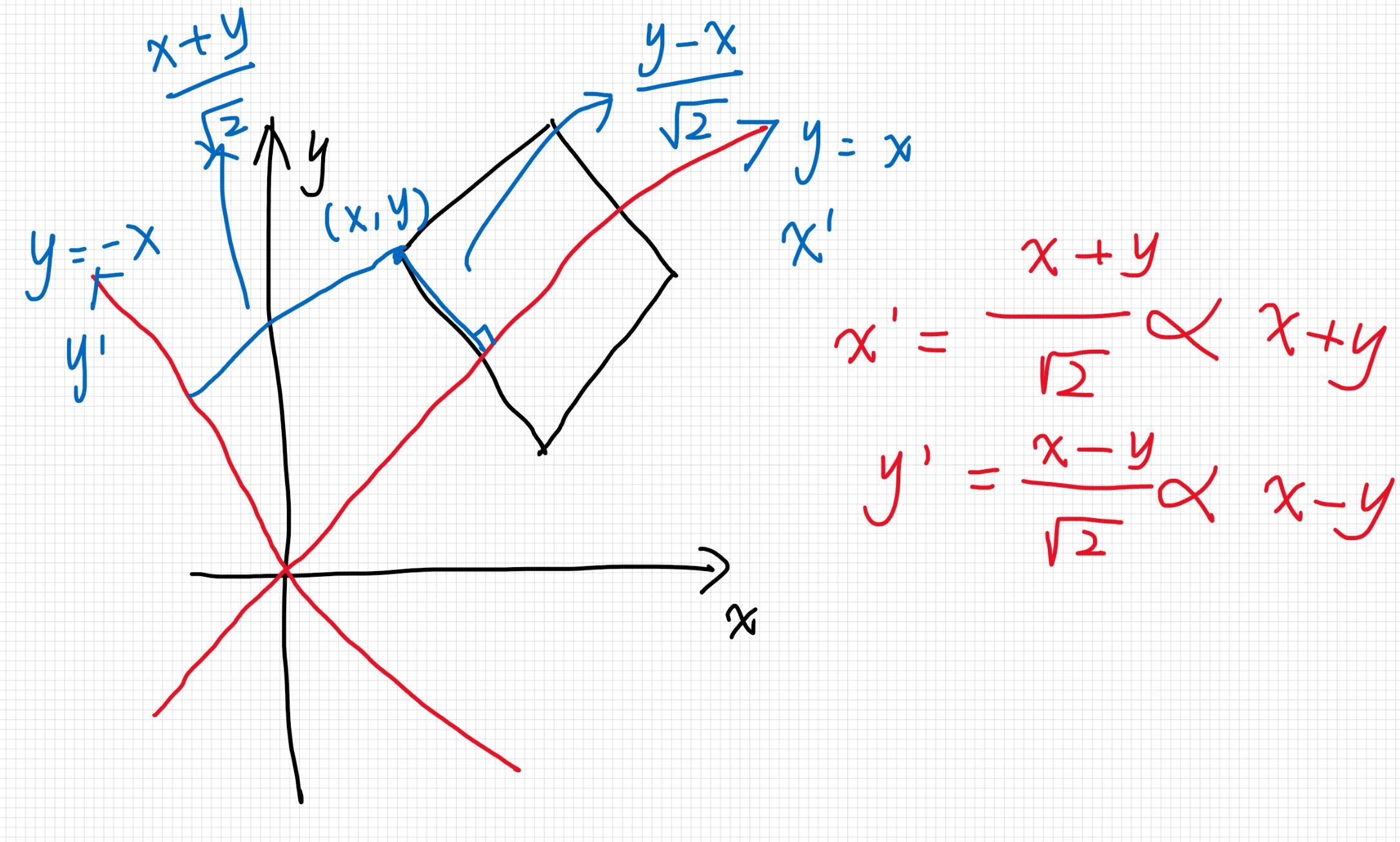
由上图可知,将原坐标系中的\((x,y)\)转化为\((x+y,x-y)\)即可、
接下来就是矩形面积并的目标了,注意取等时候还是有交的。
时间复杂度\(O(Tlog_2 n)\)
# include <bits/stdc++.h>
# define int long long
using namespace std;
struct node {
int x,y;
}a[5];
struct rec{
node a,b;
}b[5];
inline int read(){
char ch=getchar();int x=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int cx(int x,int y) {
return x-y;
}
int cy(int x,int y) {
return x+y;
}
bool get(int i,int j) {
int x[4],y[4];
x[0]=cx(b[i].a.x,b[i].a.y); y[0]=cy(b[i].a.x,b[i].a.y);
x[1]=cx(b[i].b.x,b[i].b.y); y[1]=cy(b[i].b.x,b[i].b.y);
x[2]=cx(b[j].a.x,b[j].a.y); y[2]=cy(b[j].a.x,b[j].a.y);
x[3]=cx(b[j].b.x,b[j].b.y); y[3]=cy(b[j].b.x,b[j].b.y);
if(max(x[0],x[1])<min(x[2],x[3])||max(x[2],x[3])<min(x[0],x[1])||max(y[0],y[1])<min(y[2],y[3])||max(y[2],y[3])<min(y[0],y[1])) return 0;
else return 1;
}
bool check(int L) {
for (int i=1;i<=4;i++) {
b[i].a.x=b[i].b.x=a[i].x;
b[i].a.y=a[i].y+L; b[i].b.y=a[i].y-L;
}
for (int i=1;i<=4;i++)
for (int j=i+1;j<=4;j++)
if (!get(i,j)) return false;
return true;
}
signed main()
{
int t=read();
while (t--) {
for (int i=1;i<=4;i++) {
a[i].x=read(); a[i].y=read();
}
int l=0,r=1e18,ans;
while (l<=r) {
int mid=(l+r)/2;
if (check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
printf("%lld\n",ans);
}
return 0;
}
Problem H Race
给出\(n(1\leq n \leq 3\times 10^5)\)个整数\(h_i (1\leq i \leq n)\),\(n-1\)个整数\(a_i(2 \leq i \leq n)\).
给出\(q(1\leq q \leq 3\times 10^5)\)个询问\(l_i,r_i (1\leq l_i<r_i\leq n , 1\leq i \leq q)\),输出有多少组\((l,r)\)满足:
- \(l_i\leq l \leq r-1<r \leq r_i\)
- \(h_l> \max\{ h_{l+1},...,h_{r-1}\}\)
- \(a_r > \max\{ h_{l},...,h_{r-1}\}\)
考虑对所有问题离线,将所有询问放在右端点查询。
\(i\)从左往右扫一下\(1-n\),
维护一个让\(h_i\)单调递减的单调栈,栈中的所有点可能作为当前或后面的\(i\)作为右端点询问的答案。
当一个点从单调栈中弹出的时候,表示当前点在当前的\(i\)点以后(即\(r>i\))不可能作为这个\(r\)对应的左端点。
这个值弹出后,当前\(l\)对应的\(r\)(即小于等于\(i\)的\(r\))的个数将不会被更改,将其弹出加入到一个维护单点单次赋值,区间求和的数据结构中(显然可以用树状数组实现)。
另外,我们还需要一个执行区间\(+1\),可以置\(0\)并永不修改,加点的数据结构,线段树可以完成这个任务。
对于每个线段树节点维护区间和,区间删除元素个数,加法tag。
先将\(h_1\)塞入单调栈,对于\(i\in[2,n]\)从左往右扫描\(1-n\),
在单调栈里面二分找到一个最远离栈顶的位置\(p\),满足栈中当前位置对应的\(h\)值严格小于\(a_i\)的值,那么对于\(p\)到栈顶的所有\(l\)都有一个\(r=i\)可以添加,由于下标\(i\)是有序的,那么线段树对未弹出栈的元素一定是递增的一个区间,用线段树将这个区间中的所有元素(有些元素可能由于弹出栈而在线段树中删除)区间\(+1\)
扫描右区间在\(i\)的所有询问,输出线段树中的还在栈中的答案(编号为l到i的未删除数的区间和)+ 树状数组编号为l到i的弹出栈数得到区间和,将查询结果保存在对应的数组元素中。
将\(h_i\) 插入单调栈,当有元素弹出时,将线段树中的对应元素赋值为\(0\),并将删除元素个数\(+1\),在树状数组对应位置单点加上线段树上 \(l\) 到 \(i\) 的的所有未删除数的总和。
时间复杂度\(O((n+q)log_2 n)\)
# include <bits/stdc++.h>
# define int long long
# define lowbit(x) (x&(-x))
using namespace std;
const int N=3e5+10;
int n,q,top,tot;
int a[N],h[N],ans[N];
pair<int,int>s[N];
vector< pair<int,int> >qes[N];
struct Seg {
int l,r;
int res,num,tag;
}tr[N*4];
inline int read(){
char ch=getchar();int x=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void build(int x,int l,int r) {
tr[x].l=l; tr[x].r=r;
if (l==r) return;
int mid=(l+r)/2;
build(2*x,l,mid);
build(2*x+1,mid+1,r);
}
void down(int x){
tr[2*x].res+=tr[x].tag*(tr[2*x].r-tr[2*x].l+1-tr[2*x].num);
tr[2*x+1].res+=tr[x].tag*(tr[2*x+1].r-tr[2*x+1].l+1-tr[2*x+1].num);
tr[2*x].tag+=tr[x].tag;
tr[2*x+1].tag+=tr[x].tag;
tr[x].tag=0;
}
void update(int x,int opl,int opr) {
if (opl<=tr[x].l&&tr[x].r<=opr) {
tr[x].tag++;
tr[x].res+=tr[x].r-tr[x].l+1-tr[x].num;
return;
}
down(x);
int mid=(tr[x].l+tr[x].r)/2;
if (opl<=mid) update(2*x,opl,opr);
if (opr>mid) update(2*x+1,opl,opr);
tr[x].res=tr[2*x].res+tr[2*x+1].res;
tr[x].num=tr[2*x].num+tr[2*x+1].num;
}
int query(int x,int opl,int opr) {
if (opl<=tr[x].l&&tr[x].r<=opr) return tr[x].res;
int mid=(tr[x].l+tr[x].r)/2,res=0;
down(x);
if (opl<=mid) res+=query(2*x,opl,opr);
if (opr>mid) res+=query(2*x+1,opl,opr);
return res;
}
void modify(int x,int p) {
if (tr[x].l==tr[x].r) {
tr[x].res=0; tr[x].num=1;
return;
}
down(x);
int mid=(tr[x].l+tr[x].r)/2;
if (p<=mid) modify(2*x,p);
else modify(2*x+1,p);
tr[x].res=tr[2*x].res+tr[2*x+1].res;
tr[x].num=tr[2*x].num+tr[2*x+1].num;
}
int find(int key) {
int l=1,r=top,ans=0;
while (l<=r) {
int mid=(l+r)/2;
if (s[mid].first<key) ans=mid,r=mid-1;
else l=mid+1;
}
return ans;
}
struct BT {
int c[N];
void update(int x,int d) {
for (;x<=n;x+=lowbit(x)) c[x]+=d;
}
int _query(int x) {
int res=0;
for (;x;x-=lowbit(x)) res+=c[x];
return res;
}
int query(int l,int r) {
return _query(r)-_query(l-1);
}
}BT;
signed main() {
n=read();
for (int i=1;i<=n;i++) h[i]=read();
for (int i=2;i<=n;i++) a[i]=read();
build(1,1,n);
q=read();
for (int i=1;i<=q;i++) {
int l=read(),r=read();
qes[r].push_back(make_pair(l,i));
}
top=tot=0;
s[++top]=make_pair(h[1],++tot);
for (int r=2;r<=n;r++) {
int t = find(a[r]);
if (t) {
update(1,s[t].second,s[top].second);
}
for (int i=0;i<qes[r].size();i++) {
int l=qes[r][i].first,id=qes[r][i].second;
ans[id]=query(1,l,tot)+BT.query(l,r);
}
while (top&&s[top].first<=h[r]) {
BT.update(s[top].second,query(1,s[top].second,tot));
modify(1,s[top].second);
top--;
}
s[++top]=make_pair(h[r],++tot);
}
for (int i=1;i<=q;i++) printf("%lld\n",ans[i]);
return 0;
}
Problem I Toilet
有\(n(1\leq n \leq 10^4)\)个人,总共有
\(T(1\leq T\leq 10^6)\)时间,有\(a(1\leq a \leq n)\)个男志愿者,\(b(1\leq b\leq n)\)个女志愿者。
每个人有三个参数 \(F/M \ t_i\ h_i (0 \leq t_i,h_i < T)\)表示在\(t_i\)时提出上厕所加入队列中,如厕时间\(h_i\)
如果到\(T\)时间内无法去上厕所,那么在\(T\)时间时一定会起身上厕所。
输出每个人等待的时间。
厕所大模拟,只需要维护男生、女生各一个队列即可。
若队列在\(T\)时间时还有人,那么直接弹出,直到队列为空。
注意时间可能从\(0\)开始。
时间复杂度\(O(T)\)
# include <bits/stdc++.h>
using namespace std;
const int N=1e4+10;
const int M=1e6+10;
int T,n,ans[N];
int resv[2];
struct rec{
int op,t,h,id;
}toliet[N];
queue<rec>q[2];
vector<int>backv[M];
bool cmp(rec a,rec b) {
return a.t<b.t;
}
int main()
{
scanf("%d%d%d%d",&n,&T,&resv[1],&resv[0]);
for (int i=1;i<=n;i++) {
string s; int t,h;
cin>>s>>t>>h;
toliet[i]=(rec){s=="M",t,h,i};
}
sort(toliet+1,toliet+1+n,cmp);
for (int i=1;i<=n;i++) {
q[toliet[i].op].push(toliet[i]);
}
for (int time=0;time<T;time++) {
for (int i=0;i<backv[time].size();i++) {
resv[backv[time][i]]++;
}
while (q[0].size()) {
rec u = q[0].front();
if (u.t<=time&&resv[u.op]) {
ans[u.id]=time-u.t;
resv[u.op]--;
if (time+u.h<T) backv[time+u.h].push_back(u.op);
q[0].pop();
} else break;
}
while (q[1].size()) {
rec u = q[1].front();
if (u.t<=time&&resv[u.op]) {
ans[u.id]=time-u.t;
resv[u.op]--;
if (time+u.h<T) backv[time+u.h].push_back(u.op);
q[1].pop();
} else break;
}
}
while (q[0].size()) {
ans[q[0].front().id]=T-q[0].front().t;
q[0].pop();
}
while (q[1].size()) {
ans[q[1].front().id]=T-q[1].front().t;
q[1].pop();
}
for (int i=1;i<=n;i++) printf("%d\n",ans[i]);
return 0;
}
Problem J Summer Love
给出\(n,k (1\leq n ,k\leq 5\times 10^3)\)和\(n\)个元素\(a_i (1\leq i \leq n)\)
将\(a_i\)分成\(k\)份,最大化每一份最大值减去最小值值之和
定义\(f[i][j][0/1][0/1]\)表示当前遍历到\(i\)位置,已经分了\(j\)份,当前份的最大值是否\(0/1\)确定,最小值是否\(0/1\)确定。
最后的答案显然为\(f[n][k][1][1]\),
每一次转移到新的一份,必须要在前一份最大值和最小值都确定的情况下。
- \(f[i][j][0][0] = f[i-1][j-1][1][1]\) 新建一个部分,\(a_i\)不作最大值或者最小值。
- \(f[i][j][0][1] = f[i-1][j][1][1] - a[i]\)新建一个部分,\(a_i\)作最小值。
- \(f[i][j][1][0] = f[i-1][j][1][1] + a[i]\)新建一个部分,\(a_i\)作最大值。
- \(f[i][j][1][1] = f[i-1][j][1][1] +a_i - a_i\)新建一个部分,\(a_i\)作最大值和最小值。
每一次延续前一次的块,也是一种选择
- \(f[i][j][0][0] = f[i-1][j][0][0]\) 延续上一个部分,\(a_i\)不作最大值或者最小值。
- \(f[i][j][0][1] = \max \{ f[i-1][j][0][0]-a[i] , f[i][j-1][0][1] \}\) 延续上一个部分,\(a_i\)可能做最小值。
- \(f[i][j][1][0] = \max \{ f[i-1][j][0][0]+a[i] , f[i][j-1][1][0] \}\) 延续上一个部分,\(a_i\)可能做最大值。
- \(f[i][j][1][1] = \max\{f[i-1][j][0][0]+a[i]-a[j],f[i-1][j][0][1]+a[i],f[i-1][j][1][0]-a[i]\},f[i-1][j][1][1]\)延续上一个部分,\(a_i\)可能做最大值,可能做最小值,可能不作最大值或者最小值。
初始化:
- \(f[1][1][0][0]=f[1][1][1][1]=0\)
- \(f[1][1][0][1]=-a[1]\)
- \(f[1][1][1][0]=a[1]\)
- 其他\(-inf\)
使用滚动数组可以优化掉一位空间,时间复杂度为\(O(nk)\)
# include <bits/stdc++.h>
# define int long long
using namespace std;
const int N=5e3+10;
int n,k;
int f[2][N][2][2],a[N];
int max2(int x,int y,int z,int t) {
int ans = -1e18;
if (x>ans) ans=x;
if (y>ans) ans=y;
if (z>ans) ans=z;
if (t>ans) ans=t;
return ans;
}
signed main() {
scanf("%lld%lld",&n,&k);
for (int i=1;i<=n;i++) scanf("%lld",&a[i]);
memset(f,0x8f,sizeof(f));
int p=1;
f[1][1][0][0]=f[1][1][1][1]=0;
f[1][1][0][1]=-a[1];
f[1][1][1][0]=a[1];
for (int i=2;i<=n;i++,p^=1)
for (int j=1;j<=min(i,k);j++) {
f[p^1][j][0][0] = f[p][j-1][1][1];
f[p^1][j][0][1] = f[p][j-1][1][1] - a[i];
f[p^1][j][1][0] = f[p][j-1][1][1] + a[i];
f[p^1][j][1][1] = f[p][j-1][1][1];
f[p^1][j][0][0] = max(f[p][j][0][0],f[p^1][j][0][0]);
f[p^1][j][0][1] = max(max(f[p][j][0][1],f[p][j][0][0]-a[i]),f[p^1][j][0][1]);
f[p^1][j][1][0] = max(max(f[p][j][1][0],f[p][j][0][0]+a[i]),f[p^1][j][1][0]);
f[p^1][j][1][1] = max(max2(f[p][j][1][1],f[p][j][1][0]-a[i],f[p][j][0][1]+a[i],f[p][j][0][0]),f[p^1][j][1][1]);
}
printf("%lld\n",f[p][k][1][1]);
return 0;
}
Problem K Present
给出\(n(1\leq n \leq 10^5)\)和\(n\)个正整数\(a_i(1\leq a_i \leq 2^{30}-1)\)
输出删除若干个数后,剩余数的异或和最小,输出所有删除的数和剩余数最小的异或和。
显然,删除所有数后,剩余数的异或和最小,时间复杂度为\(O(n)\)
# include<bits/stdc++.h>
using namespace std;
int main()
{
int n; scanf("%d",&n);
printf("0 %d\n",n);
for (int i=1;i<=n;i++) printf("%d ",i);
puts("");
return 0;
}
也可以采用线性基解决本题。
# include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],p[31],cnt,n;
vector<int>ans;
void insert(int x) {
for (int i=30;i+1;i--) {
if (!(x>>i)) continue;
if (!p[i]) { p[i]=x; cnt++; break;}
x^=p[i];
}
}
void reinsert(int x,int key) {
memset(p,0,sizeof(p));
int rec=x;
for (int i=30;i+1;i--) {
if (!(x>>i)) continue;
if (!p[i]) {
p[i]=x;
if (i<key) ans.push_back(rec);
break;
}
x^=p[i];
}
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++) {
scanf("%d",&a[i]);
insert(a[i]);
}
if (cnt<n) {
printf("0 %d\n",n);
for (int i=1;i<=n;i++) printf("%d ",i);
} else {
int res=(1<<30),id;
for (int i=0;i<=30;i++) if (res>p[i]) {
res=p[i]; id=i;
}
for (int i=1;i<=n;i++) reinsert(a[i],id);
printf("%d %d\n",res,ans.size());
for (int i=0;i<ans.size();i++) printf("%d ",ans[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号