AGC VP 记录

如题，AGC060~AGC080

AGC072

[AGC072A] Rhythm Game

给定 $n$ 个按钮，第 $i$ 个按钮会在 $t_i$ 秒出现在 $x_i$，每个按钮会在出现 $d+0.5$ 秒后消失。玩家从坐标 $0$ 开始，可以以任意顺序按下所有按钮，每次按完按钮后需要回到坐标 $0$，求能否按完 $n$ 个按钮。

$n\le 5000,x_i,t_i,d\le 10^{12}$。

将一个按钮转化为在区间 $[t_i-x_i,t_i+x_i+d]$ 中选择一个长度为 $2x_i$ 的区间，要求所有选择的区间不交。于是可以将问题转化为有 $n$ 个任务，每个任务是 $(l_i,r_i,c_i)$，表示人物在 $l_i$ 时间派出，需要 $c_i$ 时间完成，并且需要在 $r_i$ 前完成。考虑如果所有 $l_i=0$ 怎么做，显然可以贪心按 $r_i$ 排序，然后依次完成每个任务，因为如果有两个任务的完成顺序与 $r_i$ 大小关系不符，则交换这两个任务一定不劣。

于是我们将所有任务按 $r_i$ 排序。现在有了 $l_i$ 的限制，也就可能想完成 $r_i$ 最小的任务时还没派出，所以会先去完成其他任务。但是注意到，如果完成了第 $j$ 个任务，那么所有 $i<j$ 的任务都已经派出，因为 $t_j+x_j\ge t_i+x_i\ge t_i-x_i$。于是我们的策略一定是，设当前已经完成了前 $i$ 个任务，然后完成一个任务 $j$，接着依次完成任务 $[i+1,j-1]$。

于是就可以 dp，设 $f_i$ 表示完成前 $i$ 个任务的最早时间，然后枚举 $f_i$ 从 $f_j$ 转移过来，设 $t = \max(f_j,l_i)+c_i$，首先要求 $t\le r_i$。然后依次枚举 $k\in [j+1,i-1]$，需要满足 $t+c_{j+1}+c_{j+2}+\ldots+c_k\le r_k$，记 $c_i$ 前缀和为 $s_i$，就是 $t-s_j\le r_k-s_k$。那么从大到小枚举 $j$ 的同时记录 $r_k-s_k$ 的最小值即可 $\mathcal{O}(1)$ 判断，总复杂度为 $\mathcal{O}(n^2)$。

Submission #69244722 - AtCoder Grand Contest 072

[AGC072C] Human Exercise

给定一个 $n\times n$ 的网格，重复以下操作 $k$ 次。

从 $(1,1)$ 出发走向 $(n,n)$，每次可以向下或向右走，如果两个方向都可以走，则会选择之前访问次数少的格子。如果访问次数相同，则优先选择向下。

求第 $k$ 次的路径。$n\le 100,k\le 10^{18}$

考虑求出前 $k-1$ 次后每个点经过了多少次，然后就可以模拟出第 $k$ 次的路径了。首先左上方和右下方应该是对称的，所以我们只考虑左上角的次数。首先 $(1,1)$ 一定经过了 $k-1$ 次，观察这 $k-1$ 次中有多少次往下，有多少次往右。打表发现是一次往下一次往右，继续观察发现对于一个点 $(i,j)$，一定是先往下 $i$ 次，往右 $j$ 次，并以 $i+j$ 为周期循环。所以就可以统计出每个点到达多少次了。（严格证明参考官方题解）

Submission #66828532 - AtCoder Grand Contest 072

AGC071

[AGC071A] XOR Cross Over

有一个长度为 $n$ 的序列 $a$。每次操作可以选择一个长度为 $m > 1$ 的序列 $b$，并选择一个 $1\le k < m$，设 $X = b_1\oplus b_2\oplus\ldots \oplus b_k,Y = b_{k+1} \oplus b_{k+2} \oplus \ldots \oplus b_m$，将序列分成一个长度为 $k$ 和一个长度为 $m-k$ 的序列，分别为 $b_1\oplus Y,b_2\oplus Y,\ldots,b_k\oplus Y$ 和 $b_{k+1}\oplus X,b_{k+2}\oplus X,\ldots,b_m\oplus X$。

一直操作直到每个序列长度为 $1$，求这 $n$ 个数的和的最小值。

$n\le 500$

第一反应是区间 dp，但是每个区间还需要记录这个区间整体被异或了多少，不太好做。尝试找性质，如果某次分裂中一段是奇数，那么另一段中之前整体异或的数就被抵消掉了。于是对于一个偶数长度的区间，最后分裂到每个数时，一定存在一次分裂使得另一端长度为奇数，于是就会抵消掉之前异或的数，所以说对于偶数长度区间之前异或了多少是不重要的。

对于奇数长度区间，每次分裂都有一段不会保留之前的异或，所以到最后一定会恰好剩下一个数收到了影响，并且这个数等于之前异或的 $x$ 异或上整个区间的 $a_i$。于是我们设 $f_{l,r}$ 表示如果区间 $[l,r]$ 的答案，如果 $[l,r]$ 长度是奇数，那么不计算被影响的那个值的贡献。

那么考虑转移，设 $sum$ 表示当前区间的异或和：

如果区间长度是偶数，就枚举下一步在哪里分裂，$f_{l,r}\larr f_{l,k}+f_{k+1,r}+2sum[k-l+1\bmod2=1]$
否则，枚举最终剩下的数在哪里，那么一定要求 $[l,k-1],[k+1,r]$ 长度为偶数。因为我们每次要求切掉的不含 $k$ 的部分长度为偶数，所以一次性全部切完一定是最优的。于是转移为 $f_{l,r}\larr f_{l,k-1}+f_{k+1,r}$

最终答案为 $f_{1,n}$，如果 $n$ 为奇数，还要加上 $a_1\sim a_n$ 的异或和。

Submission #68463623 - AtCoder Grand Contest 071

[AGC071B] Maximum Bracket Subsequence

给定一个长度为 $k$ 的合法括号串 $T$，求有多少个长度为 $n$ 的括号串 $S$，满足 $S$ 所有长度为 $k$ 的合法括号子序列中，字典序最大的为 $T$。

$k\le 5\times 10^5,n\le 10^7$

建议升黑，要不然感觉是最困难的紫题了。

先考虑怎么求一个括号串 $S$ 中长度为 $k$ 的最长合法括号子序列，因为 $()$ 的字典序最大，所以前面选越多 $()$ 越好。我们求出最大的 $x$ 满足，找到最小的 $i$ 使得 $S[1\dots i]$ 中存在 $x$ 个 $()$ 的子序列，$S[i+1\ldots n]$ 需要存在一个长度为 $k-2x$ 的合法括号子序列。

此时还要求出 $S[i+1\ldots n]$ 中长度为 $k-2x$ 的字典序最大的括号子序列，可以考虑先将 $S[i+1\ldots n]$ 中所有不能匹配的左右括号都删掉，然后每次删去最左边的括号和与之匹配的右括号，直到剩下长度为 $k-2x$ 的序列就是字典序最大的括号子序列。

为什么这样做是对的？首先我们一定不会删去 $()$，因为如果删掉了第一步的 $x$ 就可以增加，那么考虑删第一个和第二个左括号的区别。假设括号串长成 $((s_1)s_2)$，删掉第一个和第二个左括号分别会变成 $(s_1)s_2$ 和 $(s_1s_2)$，显然删第一个一定更优。于是我们就说明了以上方法是对的，并且因为删 $()$ 是特殊的，所以才有了第一步找最大 $x$ 来去掉 $()$ 的影响。

接下来考虑倒过来做一遍上面的步骤，将 $T$ 变成某一个 $S$。首先找出 $T$ 的前面一共有多少个连续的 $()$，记为 $a$，然后求出 $a$ 个 $()$ 后面最多能拆成多少个合法的括号子串，也相当于有多少个位置前缀和为 $0$，记为 $b$。

我们将 $T$ 拆成两部分 $T_1,T_2$ 考虑，其中 $T_1$ 为前 $a$ 个 $()$。先考虑 $T_2$，首先可以每次选择一个 $T_2$ 除开头的前缀和为 $0$ 的位置，然后在最前面插入一个 $($，在选的位置插入一个 $)$。
在所有 $T_2$ 前缀和为 $0$ 的位置插入一些 $($ 和 $)$，满足所有 $)$ 在 $($ 前面。
在 $T_1$ 中插入一些左右括号（最后面不能插，最后面的已经放到上面考虑了），因为要不能记重，所以我们要定一个从 $S$ 中选出前 $a$ 个 $()$ 的规则。我们钦定这个规则为每次遇到一个 $)$ 就将其与最左边的 $($ 进行匹配。那么如果要插到 $T_1$ 最前面或者两个 $()$ 之间，就不能插 $($，因为后面会匹配到这个；如果插到某个 $()$ 中间，就不能插 $)$，因为这个 $)$ 会先匹配。

可以发现，按照上面的方式，每个合法的 $S$ 恰好会被生成一次。现在考虑计数，总共会插 $n-k$ 个括号，考虑用生成函数刻画每一步的方案数。

第一步的插入中，分是否插入了至少一个 $()$ 讨论，先看插入了至少一个，另一种情况放到后面。那么枚举一个 $i$ 表示最后一步插到了第几个除开头的前缀和为 $0$ 的位置，那么用 $j$ 个左右括号相当于将 $j-1$ 个括号放到 $i$ 个盒子中，所以生成函数为：

\[\sum_{j = 1} {j-1+i-1\choose i-1}x^{2j} = x^2\sum_{j = 0}{j+i-1\choose i-1}x^{2j} = \frac{x^2}{(1-x^2)^i} \]
第二步，假设插了 $j$ 个括号，先不分左右括号，将其放入 $b-i+2$ 个盒子中，然后选一个分界线使得左边全为 $)$，右边全为 $($，方案数为 $j+1$，所以生成函数为：

\[\sum_{j = 0}{j+b-i+1\choose b-i+1}x^j(j+1) = (\sum_{j = 0} {j+b-i+1\choose b-i+1}x^{j+1})' = (\frac{x}{(1-x)^{b-i+2}})' = \frac{(b-i+1)x+1}{(1-x)^{b-i+3}} \]
第三步，因为每个位置能插什么括号是确定的，所以就是将 $j$ 个括号放入 $2a$ 个盒子中，生成函数为 $\frac{1}{(1-x)^{2a}}$。

总的生成函数为：

\[\begin{aligned} &\frac{1}{(1-x)^{2a}}\sum_{i = 1}^b\frac{x^2}{(1-x^2)^i}\times\frac{(b-i+1)x+1}{(1-x)^{b-i+3}} \\ =& \frac{x^2}{(1-x)^{2a+b+3}}\sum_{i = 1}^b\frac{(b-i+1)x+1}{(1+x)^{i}} \\ =& \frac{x^2}{(1-x)^{2a+b+3}}\sum_{i = 1}^b(\frac{b-(i-1)}{(1+x)^{i-1}} - \frac{b-i}{(1+x)^i}) \\ =& \frac{x^2}{(1-x)^{2a+b+3}}(b-0) = \frac{bx^2}{(1-x)^{2a+b+3}}\\ \end{aligned} \]

第一步不插入任何括号的生成函数也可以类似推得，相当于将第二步的 $i$ 设为 $1$，第三步不变，为：$\frac{1}{(1-x)^{2a}}\frac{bx+1}{(1-x)^{b+2}}$。

设 $m = n-k$，所以最终答案为：

\[\begin{aligned} [x^m](\frac{bx^2}{(1-x)^{2a+b+3}}+\frac{bx+1}{(1-x)^{2a+b+2}}) &= [x^m]\frac{(b-1)x+1}{(1-x)^{2a+b+3}} \\ &= [x^{m-1}]\frac{b-1}{(1-x)^{2a+b+3}}+[x^m]\frac{1}{(1-x)^{2a+b+3}} \\ &= (b-1){m+2a+b+1\choose 2a+b+2}+{m+2a+b+2\choose 2a+b+2} \end{aligned} \]

另外，如果 $b=0$ 要特殊处理，相当于 $T$ 全是 $()$，此时在后面插任何东西都可以，方案数为：

\[\sum_{i = 0}^n 2^i {n-i+2a-1\choose 2a-1} \]

Submission #69389273 - AtCoder Grand Contest 071

[AGC071C] Orientable as Desired

给定一个 $n$ 个点 $m$ 条边的无向简单连通图，判断是否存在一个长度为 $n$ 的非负整数序列 $(x_1,x_2,\ldots,x_n)$，满足：

$x_i\le deg_i$，$deg_i$ 表示点 $i$ 的度数。

不存在一种给原图的每条边定向的方案，使得 $\forall 1\le i\le n$，满足点 $i$ 的出度或入度等于 $x_i$。

$n,m\le 2\times 10^5$

先考虑一些特殊情况，比如 $x$ 全为 $0$，那么一定是将 $n$ 个点划分为两个集合，一个集合全部连向另一个集合，即要求原图是一个二分图，所以如果原图不是二分图就可以直接输出 YES。

接下来考虑 $x$ 中某一位有值，其余为全是 $0$。不妨设 $x = (y,0,0,\ldots)$，我们尝试找到一种定向方案满足这个 $x$。将原图去掉 $1$，会形成一些连通块，显然每个连通块都是二分图，所以只有两种定向方案。设 $1$ 在每个连通块中的度数分别为 $a_1,a_2\ldots,a_k$，那么我们需要能找出一些 $a_i$ 使得和为 $y$，显然 $y$ 可以取遍 $0\sim deg_1$，所以我们要求 $a_1,a_2,\ldots,a_k$ 能凑出所有 $0\sim deg_1$。于是如果有一个 $u$，满足 $u$ 的 $a_1\ldots a_k$ 不能凑出 $0\sim deg_u$ 中的所有数，我们就找到了一种 $x$。

接下来大胆猜测如果不满足上述条件，则一定不存在 $x$，相当于对于所有 $x$ 都存在边的定向方案。考虑证明，我们建出原图的圆方树，那每个方点就有两种定向方案。然后从根节点往下 dfs，每次到一个圆点 $u$ 时，只有其父亲的方点被定向了，则我们要定向 $u$ 的所有儿子方点，设 $u$ 在每个方点的度数为 $a_1\ldots a_k$，其中父亲方点为 $a_1$，有 $a_1\ldots a_k$ 能凑出 $0\sim deg_u$ 的所有数。则我们需要在 $a_2\ldots a_k$ 中选出一些 $a_i$ 满足和为 $x_u$ 或 $x_u-a_1$，这一定是存在的，因为如果不存在的话，再来一个 $a_1$ 也凑不出 $x_u$，与条件矛盾。

所以无解的充要条件为对于所有点 $u$，满足 $a_1\ldots a_k$ 能凑出来 $0\sim deg_u$ 的所有数，这个判断是容易的，将 $a_i$ 排一遍序，那么充要条件为 $\forall 1\le i\le k,\sum\limits_{j=1}^{i-1}a_j\ge a_i-1$。求 $a_i$ 用 tarjan 即可，复杂度为 $\mathcal{O}(n+m\log m)$。

Submission #59336206 - AtCoder Grand Contest 060

AGC070

[AGC070A] Multiples in the String

提交答案题，求一个正整数 $X$ 和字符串 $S$，满足：

$10^{50}\le X < 10^{5000}$，$S$ 由数字 $0\sim 9$ 构成，且长度不超过 $5000$

对于所有 $1\le i\le 1000$，满足 $X\times i$ 得到的十进制数是 $S$ 的子串。

$n\le 10^5$

发现限制条件非常严，如果你注意力比较好可以发现 $142857$ 乘上 $1\sim 6$ 都在 $142857142857$ 中出现过，而这个数恰好是 $\frac 1 7$ 的循环节。如果我们能找到类似的 $p$ 满足 $\frac 1 p$ 的循环节是 $p-1$ 且所有 $\frac i p$ 的循环节都是 $\frac 1 p$ 循环节的循环移位，那么就可以令 $X$ 等于这个循环节，$S$ 为 $X$ 重复两次得到的字符串。

把条件写出来，相当于 $\forall 1\le i < p,\exist k,\frac i p\equiv 10^k\times \frac 1 p\pmod 1$，两边同时乘 $p$ 得到 $i\equiv 10^k\pmod p$，也就是说 $10$ 是 $p$ 的原根。所以我们直接暴力从 $1000$ 开始找满足有 $10$ 这个原根的质数 $p$，发现第一个是 $1019$，于是就可以构造了。

Submission #68634175 - AtCoder Grand Contest 070

[AGC070B] Odd Namori

给定一棵 $n$ 个点，以 $1$ 为根的有根树，定义点 $i$ 的父亲为 $p_i$。我们定义满足以下条件的有向图 $G$ 为“好图”：

每个顶点的出度都为 1。

图中不存在偶数长度的环。

对于所有 $2 \leq i \leq N$ 的 $i$，$G$ 中不包含边 $i \to p_i$。

计算所有可能的“好图” $G$ 中 $2^{\text{环的数量}}$ 的总和，对 $998244353$ 取余。

神仙题。

把偶环权值看成 $0$，奇环权值看成 $2$，根据经典 trick，如果一个东西出现了 $c$ 次贡献为 $x^c$，那么可以钦定一些地方出现，贡献为 $(x-1)^c$。所以我们可以钦定一些环，则偶环贡献为 $-1$，奇环贡献为 $1$。假设我们钦定环上所有点构成的集合为 $S$，那么其他点就可以任意连，贡献是好算的，即 $1$ 能连的点数为 $n$，其余为 $n-1$。

接着考虑 $S$ 内部会连成很多环，我们先不考虑不能出现 $i\to p_i$ 的限制，然后惊人的注意到：设集合 $S$ 内编号最小和次小的点分别为 $x,y$，那么交换 $x,y$ 连向的点一定会使总的权值取反（可以枚举所有情况，发现偶环数量奇偶性一定会改变）。于是只有当 $S$ 中有一个点时，贡献为 $1$，否则为 $0$。

接着考虑 $i\to p_i$ 的限制，相当于钦定 $c$ 条 $i\to p_i$ 的边必须选，那么贡献就要乘上 $(-1)^c$。钦定一些边相当于合并一些点，如果我们钦定的边构成了两个及以上的联通块，那么根据上面的结论贡献一定为 $0$。于是我们钦定的所有边一定构成了一条祖先链，并且贡献为 $(-1)^c\times (-1)^{(c+1)+1}=1$（一个是容斥系数，一个是奇偶环的系数）。

所以问题就变成了任意选一条祖先链，贡献为其他点连边方案的乘积之和。接下来就好算了，先处理所有包含 $1$ 的祖先链，然后统计有多少条祖先链长度为 $i$，相当于对 $d_i$ 的桶做一遍后缀和，于是就可以计算答案了。

Submission #68640488 - AtCoder Grand Contest 070

[AGC070C] No Streak

Alice 和 Bob 进行了 $n$ 次猜拳。每次猜拳的可能结果包括「Alice 胜」、「Bob 胜」和「平局」。计算符合以下条件的猜拳结果有多少种，对 $10^9+7$ 取模：

在 $n$ 次对战中，Alice 赢了 $a$ 次，而 Bob 赢了 $B$ b 次。

Alice 不会连续赢两次，除非中间有平局。

Bob 也不会连续赢两次，除非中间有平局。

在任一时刻，Alice 的累积胜场数不能少于 Bob 的累积胜场数。换句话说，对于每一次猜拳结束后（从第 1 次到第 $n$ 次），Alice 的胜场数始终大于或等于 Bob 的胜场数。

$n\le 2\times 10^7$

相当于从 $(0,0)$ 走到 $(a,b)$，每次可以向右走、向上走、停留，不能连续向右或向上走两次，并且不能越过 $y=x$ 这条线。

优先考虑不能越过 $y=x$ 这条线的限制，考虑反射容斥，将第一次碰到 $y=x+1$ 后的路径翻折，相当于走到了 $(b-1,a+1)$。但是我们不能直接减去走到 $(b-1,a+1)$ 的方案数，因为有可能本来没有连续走两次的方案翻着后出现了连续走两次，反之也有可能。设 $f(a,b,c)$ 表示从 $(0,0)$ 走到 $(a,b)$，中间有 $c$ 次停留。那么所有碰到了 $y=x+1$ 并且没有出现连续走两次的方案有以下几种情况：

原来向上走碰到了 $y=x+1$ 后又马上向右走了一步，那么翻折后就不合法了，于是我们少向上走一次，相当于走到 $(b-1,a)$，然后在每个方案第一次碰到 $y=x+1$ 时插入一个向上走，而且正好因为上一步一定是向上走所以限制了插入后的那一步不能上向上走，方案数为 $f(b-1,a,c)$。
原来向上走碰到了 $y=x+1$ 后停留了一次，下一步是停留或者向上，那么相当于少一次停留，在每个方案第一次碰到 $y=x+1$ 时插入一个停留，方案数为 $f(b-1,a+1,c-1)$。
原来向上走碰到了 $y=x+1$ 后停留了一次，下一步是向左，那么我们要少一次停留和向上，方案数为 $f(b-1,a,c-1)$。

于是答案就是 $f(a,b,c)-f(b-1,a,c)-f(b-1,a+1,c-1)-f(b-1,a,c-1)$。接下来考虑怎么求 $f(a,b,c)$。相当于求有多少个序列包含 $a$ 个 A，$b$ 个 B，$c$ 个 C，并且没有出现 AA，BB。考虑先放入所有 A，然后插入 C，再插入 B，我们枚举插入 A 和 C 后 A 形成了多少个连续段。假设形成了 $i$ 个连续段，总方案数分为三部分：

将 $a$ 个 A 划分为 $i$ 段，方案数 ${a-1\choose i-1}$。
将 $c$ 个 C 插入，我们先给序列两端多放一个 C，于是问题变成了将 $c+2$ 个 C 划分为 $i+2$ 段，方案数为 ${c+1\choose i+1}$。
将 $b$ 个 B 插入，首先每个 AA 间必须放一个 B，于是 B 还剩下 $b-(a-i)$ 个，然后考虑有多少个位置可以放剩下的 B。一开始如果没有 C 那么有 $i+1$ 个位置，每多一个 C 就会多一个位置可以放 B，于是侯选位置有 $i+1+c$ 个，方案数为 ${i+1+c\choose b-(a-i)}$。

于是 $f(a,b,c)$ 可以 $\mathcal{O}(a)$ 计算，总复杂度为 $\mathcal{O}(n)$。

Submission #68635881 - AtCoder Grand Contest 070

AGC069

[AGC069A] Schedule Optimization

高桥君打算举办一个为期 $10^9$ 天的淘汰制比赛。参赛选手共有 $2^n$ 人，分别称为选手 $1$、$\ldots$、选手 $2^n$。选手 $i$ 计划在第 $l_i$ 天到第 $r_i$ 天之间的 $r_i-l_i+1$ 天内参赛。

首先，介绍比赛的流程。对于所有满足 $1\leq i\leq n,\ 1\leq j\leq 2^{n-i}$ 的整数对 $(i,j)$，共有 $2^n-1$ 种，这些与比赛期间的每场比赛一一对应。与 $(i,j)$ 对应的比赛由以下两位选手进行对决，决出胜者和败者：

当 $i=1$ 时，由选手 $2j-1$ 与选手 $2j$ 对战；

当 $i\geq 2$ 时，由与 $(i-1,2j-1)$ 对应比赛的胜者和与 $(i-1,2j)$ 对应比赛的胜者对战。

每场比赛只要决定对战的两位选手所需的所有前置比赛都已完成，且这两位选手都在比赛期间内，即可立即进行。特别地，同一位选手在同一天可以参加多场比赛。与 $(n,1)$ 对应的比赛称为决赛，完成这场比赛即为本次比赛的目标。

为了顺利完成决赛，高桥君可以采取以下措施：

指示裁判，随意决定每场比赛的胜者；

向各选手支付报酬，调整他们的参赛日程。如果让选手 $i$ 在第 $l'_i$ 天到第 $r'_i$ 天参赛，则需支付 $|l_i-l'_i|+|r_i-r'_i|$ 日元。这里，$l'_i,\ r'_i$ 是满足 $1\leq l'_i\leq r'_i\leq 10^9$ 的整数。

请你求出高桥君为调整选手日程所需支付的最小总金额。

$n\le 18,1\le l_i\le r_i\le 10^9$

让两个区间 $[l_1,r_1],[l_2,r_2]$ 的选手进行比赛，要求两个区间有交，并且会合并出一个新区间 $[\max(l_1,l_2),\max(r_1,r_2)]$。相当于要调整初始的区间使得每次合并的两个区间都合法。

对于第一次两个区间 $[l_1,r_1],[l_2,r_2]$，如果两个区间有交，显然直接合并即可。如果无交，不妨设 $r_1 < l_2$，那么显然我们将 $l_2$ 调为 $r_1$ 代价最小并且得到的区间最大，是最优的。然而对于后面的合并，将 $l$ 调小意味着要将所有初始的区间的 $l$ 都调小，也就是说每次调小 $1$ 代价不一定为 $1$，但将 $r$ 调大代价就是 $1$。

于是我们对于每个合并到某一步的区间 $[l,r]$，再维护一个递增的 vector，所有当前所有左端点构成的集合，也就是说在调整的时候每遇到一个数代价就要 $+1$。于是在合并两个区间时，如果有交就直接合并，否则我们取 $[l_2,r_2]$ 的 vector 中最大的那个数 $x$，将 $r1,l2$ 都调成 $x$ 一定是当前最优的，然后将 $x$ 删去，将原来的 $r1$ 加入。一直合并到根即可。

Submission #68648273 - AtCoder Grand Contest 069

[AGC069B] Pair Guessing

给定一个 $n\times n$ 的 01 矩阵，甲和乙在上面玩游戏，流程如下：

甲选择一个满足 $a_{i,j}=1$ 的 $(i,j)$

乙有 $n$ 次机会进行提问，每次可以询问一个 $(i',j')$，甲会回答是否有 $i=i'\or j=j'$。

乙需要回答 $(i,j)$ 是什么

你需要判断，无论甲选择哪个 $(i,j)$，乙是否都有合适的策略回答出 $(i,j)$ 是什么。

$n\le 500$

不妨设乙第一次选择了 $(1,1)$，如果回答 0，那么就可以去掉矩阵的第一行第一列，一直询问直到甲回答 1。此时如果第一行第一列中全是 $1$，那么乙就一定猜不出来（除非只剩一个 $1$），否则，乙可以选择含 $0$ 的那列或行，然后剩下的一个一个猜一定能猜出来。

于是问题变成了每次选择矩阵中的一行一列，如果这一行一列中包含 $0$，就可以删去这一行一列，求能否将矩阵删到只剩一个数。那么对于所有 $a_{i,j}=0$ 的 $(i,j)$，将第 $i$ 行向第 $j$ 列连边，对于每个连通块，找到一棵生成树，从叶子依次往上删，一共可以删 $siz-1$ 次。所以我们统计所有连通块的 $siz-1$ 之和 $sum$，然后判断是否有 $sum=n-1$ 即可。

但是还有个 cornercase（极为隐蔽的 corner），比如下面这个矩阵：

011
111
111

如果问 $(1,1)$ 后回答了否，我们可以通过问 $(1,2),(2,1)$ 来唯一确定点的位置。也就是说如果 $sum = n-2$ 且 $n > 2$ 那么也是合法的。

Submission #68648714 - AtCoder Grand Contest 069

[AGC069D] Tree and Intervals

给定 $n$ 和质数 $p$，有一棵 $n$ 个点的有标号无根树，每条边连接了 $a_i,b_i$，定义一个长度为 $n-1$ 的序列 $x$，其中 $x_j$ 为有多少条边满足 $\min(a_i,b_i)\le j < \max(a_i,b_i)$。求有多少种不同的 $x$，答案对大质数 $p$ 取模。

$n\le 500$

有一个惊人的转化，我们将 $[1,i]$ 中的点染为黑色，其余点为白色，那么 $x_i$ 就表示有多少条边两端是异色的。初始时所有点为白色，我们按 $1\sim n$ 的顺序将点染为黑色，染到 $i$ 时，设 $x,y$ 分别表示黑色，白色连通块数，那么边数就是 $x+y-1$。

考虑什么样的 $(x,y)$ 数列是可以生成出来的，显然 $i$ 从 $0$ 到 $n$ 时 $(x,y)$ 会从 $(0,1)$ 变为 $(1,0)$。我们将一个点染黑时，设这个点周围有 $p$ 个点是黑色，$q$ 个点是白色，那么 $x$ 会增加 $1-p$，$y$ 会增加 $q-1$，并且 $p+q$ 就是这个点的度数。所以如果一个 $(x,y)$ 变成了 $(x',y')$，则有 $x'\le x+1,y'\ge y-1$，并且因为 $p+q > 0$，所以不能有 $(x',y') = (x+1,y-1)$。当然还有 $\forall 1\le i < n,x_i\ne 0,y_i\ne 0$。

如果以上条件都满足，那么每个点的度数都确定了，并且 $\sum p+q = \sum deg_u = 2n-2$，所以可以大胆猜测这一定可以构成一棵树，具体证明不太会（

那么考虑如何判断一个序列能否被生成，每次相当于给定了 $x+y$ 是多少。我们发现，$x$ 是可以一下减少很多，而 $y$ 可以一下增加很多。所以如果 $x+y$ 一定，那么 $x$ 小 $y$ 大的 $(x,y)$ 下一步能到达的 $(x',y')$，$x$ 大 $y$ 小的 $(x,y)$ 下一步一定也可以到达，所以我们每次取下一步能到的 $(x',y')$ 中 $x'$ 最大的那个，即可判断一个序列能否被生成。

于是就有 dp，设 $f_{i,j,k}$ 表示考虑了 $1\sim i$，此时 $x=j,y=k$，并且是能取到的 $(x,y)$ 中 $x$ 最大的，转移枚举下一个 $x'+y'$ 是多少，然后算出 $x',y'$ 即可，复杂度为 $\mathcal{O}(n^4)$。发现这个每次是一个矩形加，所以可以二维差分数组，复杂度为 $\mathcal{O}(n^3)$。

Submission #69429980 - AtCoder Grand Contest 069

AGC068

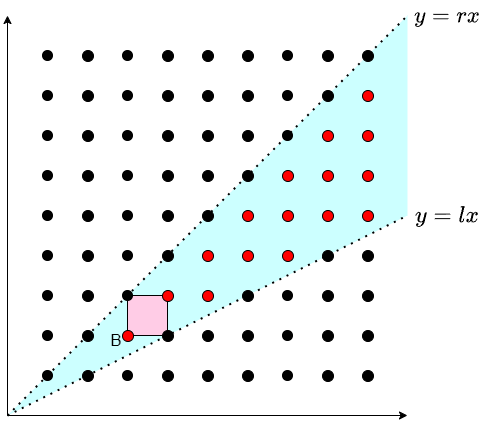
[AGC068A] Circular Distance

有一个周长为 $L$ 的圆，圆周上等间隔地站着 $L$ 个人。我们将这些人按顺时针方向编号为 $0,1,\cdots,L-1$。现在要从这 $L$ 个人中选出 $n$ 个人。对于一种选法，定义其代价如下：

对于从 $n$ 个人中任选的每一对两人，计算其中一人沿圆周移动到另一人位置的最短距离。所有这些距离的最大值即为该选法的代价。

请计算所有选法的代价之和，对 $998244353$ 取模。

$2\le n\le l\le 10^6$

牛逼题，用了好多经典转化。

设 $f_i$ 表示代价 $\le i$ 的方案数，答案即为 $\sum\limits_{i=1}^{\lfloor\frac l 2\rfloor}(f_i-f_{i-1})i$。接下来考虑如何计算 $f_d$。

不妨钦定必须选 $0$，那么将每个方案旋转 $L$ 次都可以贡献到某一个方案上，而对于一个方案最终会被贡献 $n$ 次，于是将最终答案乘 $\frac L n$ 即可。首先特判掉 $d=\lfloor\frac l 2\rfloor$，此时答案为 ${L-1\choose n-1}$。

接着，因为必须选 $0$，并且所有距离都不超过 $d$，那么剩下的点必须在 $[1,d]$ 或 $[L-d,L-1]$ 中选择，并且两个区间内的点距离一定 $<d$，所以只有两个区间之间有限制。对于一个 $x\in[L-d,L-1]$，如果选择了 $x$，那么 $[x+d+1-l,x-d-1]$ 就不能选择了。设 $len=L-2d-2$，如果我们将 $x$ 顺时针移动 $d+1$ 的距离，那么选了 $x$ 就不能选择 $[x,x+len]$ 了。

所以将 $[L-d,L-1]$ 顺时针移动 $d+1$，发现正好是 $[1,d]$。也就是说我们要在 $[1,d]$ 中一共选择 $n-1$ 个点，然后染黑白色，满足对于每个黑点的位置 $x$，$[x,x+len]$ 中没有白点，求方案数。考虑枚举有多少个黑点后面是白点，假设有 $i$ 个，那么有 $i$ 段就不能填东西了，我们把这些位置移除，那么选法为 ${d-i\times len\choose n-1}$。

接下来要将 $n-1$ 个点黑白染色，要求恰好有 $i$ 个黑点的下一个位置是白点。我们给序列最开始补一个白点，最后面补一个黑点，那么条件可以转化为恰好有 $2i+2$ 段黑白连续段。于是方案数为将 $n+1$ 个点划分为 $2i+2$ 段，方案数为 ${n\choose 2i+1}$。枚举 $i$，单次就可以 $\mathcal{O}(\frac L d)$ 计算了。所以总复杂度为调和级数 $\mathcal{O}(n\ln n)$。

Submission #68818674 - AtCoder Grand Contest 068

[AGC068B] 01 Graph Construction

如果两个 01 串 S, T 的 0 和 1 的数量分别相等，那么设 S, T 生成的图为：

将 S 中的 0 和 T 中的 0 一一对应连边。

将 S 中的 1 和 T 中的 1 一一对应连边

给定一个长度为 $n$ 的序列 $a$，你需要构造两个 01 串 S, T，满足：

S, T 的 0 和 1 的数量分别相等

$|S|\le 10^5$

S, T 生成的图中 $\forall 1\le i,j\le n$，$i,j$ 在同一连通块内当且仅当 $a_i=a_j$

$n\le 100$

初始时 $S$ 全为 $0$，$T$ 全为 $1$，有个两个排列 $p,q$ 初始都为 $1\sim n$。那么将 $S,T$ 后面都添加一个 $0$ 就相当于将 $p$ 循环移位一次；将 $S$ 后添加一个 $1$，$T$ 后添加一个 $0$ 就相当于将 $p_1,q_1$ 连边，然后两个排列都删去第一位。于是我们可以在 $\mathcal{O}(n^2)$ 次数内让每个 $i$ 都连向 $p_i$，其中 $p_i$ 是某个排列。那么将每个连通块看成一个置换环即可。

Submission #68817774 - AtCoder Grand Contest 068

[AGC068C] Ball Redistribution

有 $n$ 个编号为 $1\sim n$ 的球和 $n$ 个编号为 $1\sim n$ 的盒子，初始时你可以选择每个球放入哪个盒子，然后依次对 $1\sim n$ 执行以下操作：

如果盒子 $i$ 中没有球，则跳过。

否则，你可以按任意顺序排列盒子 $i$ 中的球，设排好后的顺序依次为 $x_1,x_2,\ldots,x_k$，则对于每个 $1\le j\le k$，将球 $x_j$ 放入盒子 $x_{j\bmod k+1}$ 中。

给定最终状态中每个球在哪个盒子中，你需要确定是否存在一种初始的状态和操作顺序能得到最终状态。

$n\le 2.5\times 10^5$

考虑倒着做，然后 $i$ 向所在的盒子编号 $p_i$ 连边，会得到一个内向基环树森林。从 $n\to 1$ 依次考虑，每次相当于可以将一个环拆掉让其全部连向 $i$。我们发现到一个 $i$ 时，如果有一个不在环上的点连向了 $i$，那么就无法操作了。否则如果有环上的点连向 $i$，则必须操作这个环，如果没有点连向 $i$，那么我们就可以任选一个环进行操作或者不操作。

这个时候就非常考验注意力了，任选一个环进行操作自由度太大了，我们可以弱化为只能拆掉所在的内向基环树森林中的环。然后模拟一下这种情况下的条件是什么，可以发现对于一个点 $u$，如果 $u$ 的所有儿子 $v$ 的子树最大值都大于 $u$，那么等操作到 $u$ 时 $u$ 一定处于环或叶子上。

进一步发现，这个条件也是必要条件，因为如果有一条边 $u\to v$ 满足 $u$ 不是环上节点并且 $u$ 子树内最大值 $<v$，那么操作到 $v$ 时 $u$ 子树内一定没有动过，所以一定不合法。即这是一个充要条件，$\mathcal{O}(n)$ 判断即可。

Submission #68880539 - AtCoder Grand Contest 068

[AGC068D] Sum of Hash of Lexmin

给定一棵 $n$ 个点的树，每个点父亲编号小于自己。定义一个排列 $p$ 是好的，当且仅当 $p$ 不能通过若干次以下操作得到一个比 $p$ 字典序小的排列：

对于相邻两个数，如果这两个数在树上呈祖先关系，则可以交换这两个数。

给定 $B$，定义 $f(p) = \sum\limits_{i=1}^nB^{i-1}p_i$，求所有好的排列的 $f(p)$ 之和。

先考虑一个不好的排列有什么性质。如果 $p$ 通过操作后得到了一个字典序更小的 $p'$，设 $i$ 是第一个 $p_i\ne p'_i$ 的位置，则 $p'_i < p_i$。设 $j$ 表示 $p$ 中 $p'_i$ 的位置，那么 $p'_i$ 一定从 $j$ 依次交换到了 $i$，相当于和 $p_i,p_{i+1},\ldots,p_{j-1}$ 都有祖先关系。因为最终 $p'_i < p_i$，那么从右到左的交换过程中，一定存在至少一次是和 $u$ 子树内的点换，找到最右边的一次 $x$，则一定满足 $p_x$ 在 $p_{x+1}$ 子树内。于是这是必要条件，并且显然这是个充分条件，因为开局交换这两个数就得到字典序更小的排列了。所以我们得到一个排列是好的当且仅当不存在 $i$ 满足 $p_i$ 在 $p_{i+1}$ 子树内。

接下来计数，考虑容斥，钦定一些位置 $i$ 满足 $p_i$ 是 $p_{i-1}$ 祖先，于是会形成很多祖先链。我们可以枚举 $u$，求 $u$ 在所有排列中的贡献，那么在 $u$ 左边放一个数会有 $B$ 的贡献，右边是 $1$ 的贡献。设 $f_{i,j,k}$ 表示考子树 $i$ 内，$u$ 左边放了 $j$ 条链，右边放了 $k$ 条链的答案（钦定了每条链内和链间的顺序，$j,k$ 都不包括 $u$ 所在的链）。转移时考虑 $i$ 放在哪，如果 $i\ne u$，有以下几种情况：

$i$ 接在左边的某条链上，贡献为 $-jB$。
$i$ 接在右边的某条链上，贡献为 $-k$。
$i$ 放在左边，自己单独成一条链，贡献为 $(j+1)B$。
$i$ 放在右边，自己单独成一条链，贡献为 $k+1$。
如果 $u$ 在 $i$ 子树内，则 $i$ 还可以接在 $u$ 所在的链上，贡献为 $-1$。

如果 $i=u$，那么转移有以下几种情况：

$u$ 接在左边最后一条链上，那么链数会减一，$f_{i-1,j,k}\larr -f_{i,j,k}\times u$
$u$ 单独成一条链，$f_{i,j,k}\larr f_{i,j,k}\times u$

然后在做上述转移前，要先将子树的 dp 值合并起来，因为两个子树左右的链可以以任意顺序合并，所以是 $f_{u,i+x,j+y}\larr f_{u,i,j}\times f_{v,x,y}\times {i+x\choose i}{j+y\choose j}$。这样子整个的复杂度为 $\mathcal{O}(n^5)$。

可以发现没有必要枚举 $u$，我们可以多记录一维 0/1 表示我们要计算的 $u$ 是否在子树内，那么在每个点将 0 贡献到 1 就表示 $u=i$，其余转移相同，复杂度为 $\mathcal{O}(n^4)$。

Submission #69243531 - AtCoder Grand Contest 068

[AGC068E] Sort and Match

给定一个 $n\times n$ 的矩阵 $a$，定义一个长为 $m$ 的序列 $x$ 的权值为，设 $y$ 为 $x$ 排序后的结果，权值为 $\prod\limits_{i=1}^m a_{x_i,y_i}$。

对于每一个 $1\le k\le n$，求出所有长度为 $m$、值域在 $[1,n]$ 内、 $x_1=k$ 的序列的权值之和。对 $998244353$ 取模。

$n,m\le 50$

牛逼题。

对于一个序列 $x$，和排序后的序列 $y$，连边 $y_i\to x_i$，边权为 $a_{x_i,y_i}$，那么对于每个连通块应该都有欧拉回路，因为 $y$ 是 $x$ 的一个置换。尝试对图进行计数，发现每个序列一定对应了一张图，但一张图可能对应了多个序列。

如果给定了一张 $m$ 条边的图，并且每个连通块都有欧拉回路，那么序列 $y$ 就唯一确定了（数每个点的出度）。对于 $y$ 中同一种数的区间，我们只知道序列 $x$ 这段区间的数构成的可重集，但不知道具体顺序。于是我们可以钦定每个点的出边顺序，相当于钦定了这些是怎么排的。相当于一个每个连通块有欧拉回路的图，知道了每个点的出边顺序，那么一定可以唯一对应一个序列。

于是我们可以计数欧拉回路，每个欧拉回路都对应了一个序列。但是要注意，每个连通块需要选一个点为起点，不同的连通块间不考虑顺序，于是我们可以选某个连通块内编号最小的点作为起点，然后走一圈回来。然后第二次走的时候选择的起点需要 $\ge x$，这样就保证了不算重。此时从小到大 $dp$，设 $f_{i,j,s}$ 表示当前路径起点为 $i$，走到了 $j$，用了 $s$ 条边，转移即可。

最后考虑 $x_1=k$ 的限制，我们可以将整个 dp 倒过来，然后在钦定最后一条边时贡献进答案即可。

Submission #61874946 - AtCoder Grand Contest 068

AGC067

[AGC067A] Big Clique Everywhere

给定一个 $n$ 个点 $m$ 条边的简单无向图，判断此图是否满足以下条件：

对于任意一个 $\{1,2,\ldots,n\}$ 的子集 $X$，都存在一个 $X$ 的子集 $Y$ 满足 $|Y|\ge \frac{|X|} 2$ 且 $Y$ 中的点都成了一个团。

$n\le 10^5,m\le 10^6$

在补图上考虑，相当于对于任意一个子集 $X$，都存在大小 $\ge\frac{|X|}2$ 的独立集。如果补图中有奇环，那么这个奇环一定不合法；否则，补图是个二分图，对于任意一个集合 $X$，$X$ 中左部点集合和右部点集合一定有一个 $\ge\frac{|X|}2$，所以合法的充要条件就是补图是一个二分图。

补图边数可能很多，但是我们发现原图中需要至少有两个并集为 $\{1,2,\ldots,n\}$ 的团，所以 $m\ge 2{\lfloor\frac n 2\rfloor\choose 2}$，即 $m$ 是 $\mathcal{O}(n^2)$ 级别的。所以我们可以先判断是否满足边数限制，然后再判断补图是否为二分图。

Submission #68872519 - AtCoder Grand Contest 067

[AGC067B] Modifications

有一个长度为 $n$ 的序列和 $m$ 个区间 $[l_i,r_i]$ 和一个数 $C$，初始每个位置为 $0$，每次操作可以选择一个区间和一个 $[1,C]$ 内的数，并将区间内都赋值为这个数，求最后能产生多少个本质不同的序列。答案对 $998244353$ 取模。

$n,C\le 100$

考虑一个最终的序列 $a$，怎么判断其是否合法？我们可以每次选一个区间出来，如果 $a$ 在区间内所有数都相同，我们就可以把这个区间内所有数都赋值成 ?，然后一直做下去，看能否让整个序列都变成 ?。

然后套路地考虑区间 dp，设 $f_{l,r}$ 表示只考虑完全被 $[l,r]$ 包含的区间，一共有多少个最终的序列 $a$ 合法，如果这些区间的并集不为 $[l,r]$。则 $f_{l,r}=0$。直接做不太好做，考虑容斥，用 $C^{r-l+1}$ 减去不合法的方案数。即计算有多少个可能的最终的 ? 和数组成的序列，满足这个序列不全为？且不能被任意一个区间再操作，即对于任意一个区间，满足序列上这个区间中全为问号或存在两个数不同。

这个东西还是可以考虑 dp 去计算，我们发现一个位置只需要记录上一个与它不同的位置即可。设 $g_{l,r,p}$ 表示区间 $[l,r]$ 中，钦定位置 $r$ 为一个数，上一个与其不同的数的位置为 $p$。转移：

后面加了一个相同的数，枚举这个数的位置 $k$：$g_{l,k,p}\larr g_{l,r,p}\times f_{r+1,k-1}$
后面加了一个不同的数，仍然是枚举位置：$g_{l,k,r}\larr g_{l,r,p}\times f_{r+1,k-1}\times(C-1)$

然后转移的时候判断是否存在一个区间 $[l_i,r_i]$ 满足 $p < l_i\le r\le r_i < k$，如果存在就不能转移，这部分可以提前预处理。时间复杂度 $\mathcal{O}(n^4)$。

Submission #64206869 - AtCoder Grand Contest 067

[AGC067D] Unique Matching

定义 $n$ 个区间 $[l_i,r_i]$ 是好的当且仅当存在唯一一个排列 $p$ 使得 $\forall 1\le i\le n,p_i\in[l_i,r_i]$。给定 $n$ 和质数 $p$，求有多少组 $n$ 个区间是好的。

$n\le 5000$

首先如果一组区间对应的排列不是 $p_i=i$ 的排列，那么可以交换其中的某些区间来让 $p_i=i$，于是只需要求出对应 $p_i=i$ 的排列的方案数，最后乘上 $n!$。

然后考虑什么样的一个区间组是合法的。如果存在 $i,j$ 满足 $i\in [l_j,r_j],j\in[l_i,r_i]$，那么可以交换 $i,j$，于是这个方案就不合法。进一步可以通过归纳法得出，一个区间组合法，当且仅当 $\forall l_j\le i < j,j > r_i$。我们在二维平面上绘制 $2n$ 条线段，分别为 $(i,i),(r_i,i)$ 和 $(i,l_i),(i,i)$，那么合法的充要条件就是这些线段互不在除 $(i,i)$ 以外的地方相交。如图（图是盗的）：

现在假设固定了 $l_i$（即图中的缺口），设 $d_i$ 为 $i$ 后面第一个 $l_j\le i$ 的 $j$，那么 $r_i\in[i,d_i)$，有 $d_i-i$ 种取值。

我们考虑对图中的白色区域设状态计数，设 $f_{i,j}$ 表示 $\forall k\in[i,j],d_k\le j+1$ 且 $l_{j+1} < l$ 时区间 $[l,r]$ 的答案，$g_{l,r}$ 表示 $\forall k\in[i,j],d_k\le j+1$ 且 $l_{j+1} \ge l$ ，答案就是 $f_{1,n}$。

设 $k$ 表示第一个满足 $d_k=j+1$ 的 $k$，即图中第一个紫色线段能延伸到末尾的位置，那么这个位置 $k$ 可以把区间分成两个部分，这两部分是独立的，因为 $r_k$ 有 $j-k+1$ 种取值，于是有转移 $f_{i,j}\larr g_{i,k-1}\times f_{k+1,j}\times (j+1-k)$。同理有 $g_{i,j}\larr g_{i,k-1}\times f_{k+1,j}\times (j+1-k)\times(k-i+1)$，其中 $k-i+1$ 表示 $l_{j+1}\in[i,k]$，有 $k-i+1$ 种取值。

观察发现转移都只和区间长度有关，所以只需要记录 $f_i,g_i$ 表示区间长度为 $i$ 时的答案，初始化 $f_0=g_0=1$，于是转移就是：

\[f_i = \sum_{j = 1}^i g_{i-1}\times f_{i-j}\times (i-j+1) \\ g_i = \sum_{j = 1}^i g_{i-1}\times f_{i-j}\times (i-j+1)\times i \]

$\mathcal{O}(n^2)$ 做即可。如果模数可以做多项式卷积的话，可以用分治 FFT 优化到 $\mathcal{O}(n\log^2 n)$。

Submission #64200908 - AtCoder Grand Contest 067

AGC066

[AGC066A] Adjacent Difference

给定一个大小为 $n\times n$ 的矩阵 $A$ 和数字 $d$，你可以对每个数字进行加上一个数或减去一个数的操作，使得每个数字与其相邻数字的差的绝对值 $\ge d$。并且对于每个操作值的绝对值之和不超过 $\frac{dn^2}{2}$。

$n\le 500$

人类智慧。我们可以将矩阵黑白染色，然后将所有黑色格子改为 $d$ 的奇数倍，白色格子改为 $d$ 的偶数倍即可满足条件。共有两种黑白染色方式，并且这两种方式的代价之和恰好为 $dn^2$，于是总有一种方式的代价 $\le \frac{dn^2}{2}$。

Submission #68976580 - AtCoder Grand Contest 066

[AGC066B] Decreasing Digit Sums

定义 $f(x)$ 表示 $x$ 各数位之和，给定 $n$，你需要找到一个数 $k$ 满足以下条件：

$1\leq k\leq10^{10000}$

对于任意整数 $1\leq i\leq n$，有 $f(2^{i-1}k)>f(2^ik)$。

$n\le 50$

依然人类智慧。首先发现只需要做 $n=50$ 即可。数越大一般来说 $f$ 也越大，但是本题要求越来越小，所以需要找一些比较好的数。

我们发现 $5$ 这个数非常好，因为乘一次 $2$ 后会变为 $10$，而 $0$ 可以忽略。那么一个 $5^a$ 一直乘 $2$ 相当于计算的是 $f(5^a),f(5^{a-1}),\ldots,f(5^{a-k})$，数越来越小了。但是这个 $5^a$ 并不好找，因为中间可能某一步 $f$ 增大了。于是我们考虑构造一个数为 $5^a,5^{a-1}\ldots 5^1$ 拼起来，那么每次乘 $2$ 后 $f$ 一定先减少 $f(5^a)$，然后再增加 eps，而 $a$ 上界可以取到 $168$，eps 的代价可以忽略不记。

Submission #68976825 - AtCoder Grand Contest 066

[AGC066C] Delete AAB or BAA

给定一个由 A, B 构成的字符串 S，每次可以删掉 S 中连续的一段 AAB 或 BBA，删掉后 S 前后部分会拼起来，求最多能操作多少次。

$|S|\le 10^6$

注意力类题目。

对每个删除的极小段考虑（极小段相当于不能再拆分为两个独立的段分别删除），分析一个极小段能删完的必要条件是什么：

A 的数量是 B 的两倍
这一段的开头或结尾是 B，因为如果开头或结尾都是 A 并且能删完的话，一定能将这段划分为两个独立的段。

然后注意力惊人即可发现这是充分的。考虑证明，相当于要证如果一个序列开头或结尾为 B 且 A 的数量为 B 的两倍那么一定能删完，不妨设序列开头为 B，如果开头为 A 的话，将序列翻转即可。考虑归纳法：

如果序列长度为 $3$，那么一定可以删完。
否则，我们找到第一个长度 $\ge 2$ 的 A 连续段的位置，这一定是存在的，那么这个连续段的左边或右边一定有一个不是开头的 B，否则说明序列长度为 $3$。于是我们删掉这个位置，就转换为了 $len-3$ 的子问题。

于是我们就证明了这是充要条件，dp 是简单的。设 A 为 $1$，B 为 $-2$，$s_i$ 表示前缀和，$f_i$ 表示前 $i$ 个数最少能剩多少个数。那么 $j$ 能转移到 $i$ 的条件为 $s_j=s_i$，$a_{j+1},a_i$ 中有一个为 B，简单转移即可。复杂度 $\mathcal{O}(n)$。

Submission #68977499 - AtCoder Grand Contest 066

[AGC066D] A Independent Set

给定一个长度为 $n$ 的由 A, B 组成的字符串 S，保证 A 的数量 $\le \frac{n+1} 2$，交换 $S_i$ 和 $S_{i+1}$ 的代价为 $x_i$，求让 S 中所有 A 不相邻的最小代价。

$n\le 10^6$

感觉有点虚高，这个做法应该比上题自然。

我们给原序列最后加一个 B，那么最终序列一定可以划分为 ABAB...AB, BBBB 这两种序列交替出现。

设 A 为 $1$，B 为 $-1$，$s_i$ 为前缀和，设 $f_i$ 表示前 $i$ 个字符的答案。那么如果 $S_i=B$，则 $f_i\larr f_{i-1}$，否则若 $s_i=s_j$，则 $f_i\larr f_j+w(j+1,i)$，其中 $w(l,r)$ 表示将区间 $[l,r]$ 中所有 A 移动到和 $l$ 同奇偶的位置的代价。设 $sum_i$ 表示从 $1$ 交换到 $i$ 的代价，那么设区间 $[l,r]$ 中 A 的位置分别为 $b_1,b_2,\ldots,b_k$，目标位置分别为 $c_1,c_2,\ldots,c_k$，那么 $w(l,r) = \sum\limits_{i=1}^k|sum_{b_i}-sum_{c_i}|$。

但是一个 $i$ 可能从很多 $j$ 转移，并且这个 $w(l,r)$ 无法快速计算。继续观察，如果 $s_j=s_i$ 且 $(j,i)$ 中还存在一个 $k$ 满足 $s_k=s_i=s_j$，那么这两段是可以分开计算的，所以我们每次转移只需要用最近的满足 $s_j=s_i$ 的 $j$ 即可。

此时区间中所有 A 一定都是向后移动或向前移动（因为如果一个向后一个向前一定可以划分为两段），所以可以将代价写为 $|\sum\limits_{i=1}^ksum_{b_i}-\sum\limits_{i=1}^ksum_{c_i}|$，于是预处理两个前缀和就可以 $\mathcal{O}(1)$ 计算了。总复杂度为 $\mathcal{O}(n)$。

Submission #69005544 - AtCoder Grand Contest 066

AGC065

[AGC065A] Shuffle and mod K

给定一个长度为 $n$ 的数组 $a$ 和 $k$，求将 $a$ 任意重排后，$\sum\limits_{i=1}^n(a_{i+1}-a_i)\bmod k$ 的最大值。

$n\le 2\times 10^5,k\le 10^9$

根据 $(x-y)\bmod k = x-y+[x<y]k$，所以 $\sum\limits_{i=1}^n(a_{i+1}-a_i)\bmod k = a_n-a_1+k\times\sum\limits_{i=1}^{n-1}[a_i<a_{i+1}]$，记 $\sum\limits_{i=1}^{n-1}[a_i < a_{i+1}] = c$，$c$ 能取到的最大值为 $cmx$，因为 $a_n-a_1\in(-k,k)$，所以 $c\ge cmx-1$，不然一定不优，于是我们分两种情况考虑：

$c=cmx$，设 $m$ 表示每个数的最大出现次数，那么 $c$ 取到最大相当于分成最少的连续的下降段，而原序列最少划分为 $m$ 个下降段。此时再最大化 $a_n-a_1$，可以发现 $a_n$ 是一组中的最小值，$a_1$ 是一组中的最大值，所以 $a_n-a_1$ 上界为所有出现次数为 $m$ 的数中的最小值减最大值，并且这个上界是可以取到的。
$c=cmx-1$，此时我们可以划分为 $m+1$ 段，依然是最大化 $a_n-a_1$，对于出现次数不为 $m$ 的数就不放到头尾段，不会造成影响，出现次数为 $m$ 的数需要选择放到头段还是尾段，我们把这些数拉出来排序，那么 $a_n-a_1$ 能取到的就是相邻两个数的差，找这些差的最大值即可。

用 $map$ 维护，复杂度 $\mathcal{O}(n\log n)$。

Submission #69022938 - AtCoder Grand Contest 065

[AGC065B] Erase and Insert

有一个 $1\sim n$ 的排列 $p$，初始时 $p_i=i$，依次对 $i\in [1,n]$ 做以下操作：从 $p$ 中删去 $i$，再在 $p$ 的任意一个位置插入 $i$。给定最终序列 $q$，求有多少种操作方法可以使 $p$ 变成 $q$。对 $10^9+7$ 取模。

$n\le 5000$

倒着做，相当于从大到小从 $q$ 中删去 $i$ 然后插入到某个位置，那么每次插入的位置满足在所有 $i+1\sim n$ 的前面即可。于是记 $f_{i,j}$ 表示考虑了 $i\sim n$，$i$ 在 $1\sim i-1$ 的排名为 $j$。转移时，设 $i$ 在 $1\sim i$ 的排名为 $x$，那么对于 $x\le j$，有 $\forall k<j, f_{i,k}\larr f_{i+1,j}$；对于 $x > j$，有 $\forall k\le j,f_{i,k}\larr f_{i+1,j}$。前缀和优化一下即可。复杂度 $\mathcal{O}(n^2)$。

Submission #69023457 - AtCoder Grand Contest 065

[AGC065C] Avoid Half Sum

给定一个长度为 $n$ 的非负整数序列 $a$，保证 $S = \sum a_i$ 为偶数。请判断是否存在满足以下条件的长度为 $n$ 的非负整数序列对 $b$ 和 $c$。

$\forall 1\le i\le n,a_i=b_i+c_i$

对于任意长度为 $n$ 的整数序列 $x$，$\forall 1\le i\le n,x_i=a_i\or x_i=b_i$，则 $\sum x_i \ne \frac{S}{2}$。

$n\le 2\times 10^5,a_i\le 10^9$

注意力题目。

$x_i$ 为 $a_i,b_i$ 的其中一个不太好做，要让 $\sum x_i=\frac S 2$，相当于把 $a,b$ 分成两个和相等的序列，设 $d_i = |a_i-b_i|$，则每次可以选择 $-d_i$ 或 $d_i$ 使得总和为 $0$。也可以换一种理解，我们要在 $d_i$ 中选出一些数使得这些数的和为 $\frac{\sum d_i} 2$。每个 $d_i$ 可以选 $[0,a_i]$ 中任意一个与 $a_i$ 奇偶性相同的数。

我们先考虑必要条件，相当于求在不满足什么条件时一定可以选出来这些 $d_i$ 使得这些数和为总和的一半。不妨弱化一下条件，我们要求一定可以选出 $[0,\sum d_i]$ 中的任意一个数。那么考虑归纳法，设前 $k-1$ 个数已经可以凑出 $[0,\sum\limits_{i=1}^{k-1}d_i]$ 中的任意一个数，要求前 $k$ 个数能凑出 $[0,\sum\limits_{i=1}^kd_i]$ 中的所有数，即 $\sum\limits_{i=1}^{k-1}d_i\ge d_k-1$，$\sum\limits_{i=1}^{k-1} d_i$ 最小为前 $i-1$ 个数中的奇数个数，$d_k-1$ 最大为 $a_k-1$，那么可以得出条件为排序后每个 $i$ 都满足前 $i-1$ 个数中的奇数个数 $\ge a_-1$。

显然相同的数只取第一个最严的即可，所以还可以转化为所有 $<a_i$ 的奇数个数 $\ge a_i-1$，不满足这个性质显然是一个必要条件，下面我们说明这是一个充分条件。我们任意找一个满足 $<a_i$ 的奇数个数 $<a_i-1$ 的 $a_i$：

如果 $a_i$ 是奇数，对于所有偶数取 $d_j=a_j$，对于所有 $<a_i$ 的奇数取 $1$，所有 $\ge a_i$ 奇数取 $d_j=a_j$，此时如果 $d_j=a_i$ 的出现次数为偶数，就将一个 $a_i$ 的 $d_i$ 设为 $1$，考虑第一种意义（选正负号加起来为 $0$），因为有奇数个 $a_i$，所以这些数凑数来绝对值至少为 $a_i$，剩下最多 $a_i-1$ 个 $1$ 也凑不出 $0$。
如果 $a_i$ 是偶数，那么第一个 $> a_i$ 的奇数也一定符合条件，如果存在这样的 $a_i$ 就选，否则就是所有 $\ge a_i$ 的都是偶数，同上述构造。

于是所有 $<a_i$ 的奇数个数 $\ge a_i-1$ 就是一个充要条件，排序后判断即可。

Submission #69023457 - AtCoder Grand Contest 065

[AGC065D] Not Intersect

有一个圆周上依次排列着 $n$ 个点，任意两个点间共有 $n\choose 2$ 条线段，求在这 $n\choose 2$ 条线段中选出 $m$ 条，所有线段除了端点外不相交的方案数为多少。对 $10^9+7$ 取模。

$n\le 10^7,m\le {n\choose 2}$

神仙题。

前置知识：

Raney 定理：对于任意一个长为 $n$ 的数组 $a$，满足 $\sum a_i = 1$，那么 $a_i$ 的 $n$ 个循环移位互不相同且恰好有一个满足所有前缀和为正数。

证明考虑将所有 $(i,s_i)$ 画到二维平面上，然后用斜率为 $\frac 1 n$ 的直线从下往上切，选切到的第一个点作为开头，此时一定满足所有前缀非正。并且因为没有两个点在同一条斜率为 $\frac 1 n$ 的直线上，所以所有循环移位一定互不相同。

两个线段 $[l1,r1],[l2,r2]$ 相交的条件为 $l1<l2<r1<r2$。先考虑 dp，并且先假设没有 $m$ 的限制，$f_{i,j}$ 表示第 $i$ 个点时前面还有 $j$ 个点可以选。于是一个 $f_{i,j}$ 可以转移到所有 $1\le k\le j$ 的 $f_{i,k}$ 或 $f_{i+1,j+1}$，要注意不能出现两次同一个 $f_{i,j}$ 转到自己。

$f_{i,j}$ 转到自己的限制条件不太好处理，发现这种边就是相邻两个点连的边，不会对其他边有限制，于是我们可以枚举这种边的数量 $x$，那么还剩下 $m-x$ 其他的边。我们观察某个转移的路径，是从 $f_{1,0}$ 到 $f_{n,j}$，对于 $j$，每次可以选择减一个正整数或者 $+1$，最后要走到第 $n$ 列。因为我们不能选 $[1,n]$ 的区间，所以不能走到 $(n,1)$，而且因为最终终点不统一不好计算，所以我们多加一步并且钦定最后一步一定要走到 $(n,1)$，这样子保证了之前不会走到 $(n,1)$ 并且统一了了终点。

转化一下问题，有 $n-1$ 个 $+1$ 和 $m-x+1$ 个负整数，令 $k=m-x+1$，需要排列这 $n-1+k$ 个数，使得所有前缀和都是正数，并且序列总和为 $1$，这不就是 Raney 定理吗？于是求出有多少种排列，那么每个排列的贡献就是 $\frac{1}{n+k}$。我们首先将 $n-1$ 个 $+1$ 和 $k$ 个负整数组合起来，方案为 $n-1+k\choose n-1$，然后所有负数的绝对值之和为 $(n-1)-1=n-2$，相当于将 $n-2$ 个球分成 $k$ 段，方案为 ${n-3\choose k-1}$。然后从 $n$ 条相邻的边选 $x$ 条方案为 ${n\choose x}$，化简一下，答案就是：

\[\sum_{i = 0}^{\min(n, m)} {n\choose i}\frac 1 {n+m-i} {n-3\choose m-i}{n+m-i\choose n-1} \]

发现 $m$ 最大为 $2n-3$，所以与 $n$ 是同阶的，于是可以 $\mathcal{O}(n)$ 计算了。

Submission #69040491 - AtCoder Grand Contest 065

AGC064

[AGC064A] i i's

skip。Submission #69194114 - AtCoder Grand Contest 064

[AGC064B] Red and Blue Spanning Tree

给定一张 $n$ 个点 $m$ 条边的连通图，每条边有红蓝的颜色，每个点也有红蓝的颜色，求是否存在一棵生成树，使得每个蓝色的点有一条蓝色的边相连，红色同理，如果有解构造方案。

$n,m\le 2\times 10^5$

任意找出每个点合法的边，发现如果没有一条边同时满足两个点，那么一定不合法，因为总共只有 $n-1$ 条边。如果一条边同时满足两个点，那么这种边肯定是选的越多越好。我们选完这种边后，从已经满足的点出发 dfs，选这些只能满足一个点的边，则一定需要遍历所有点，否则无解。此时原图形成了一个森林，再选择其他边使得整个图联通即可。

Submission #69194523 - AtCoder Grand Contest 064

[AGC064C] Erase and Divide Game

黑板上有一些数，两个人轮流操作，每次可以选择擦除黑板上的所有奇数或所有偶数，然后将剩下的数全部除以 $2$ 向下取整，无法操作的人输。现在给定 $n$ 个区间，黑板上的数初始为所有区间内的数，问谁有必胜策略。

$n\le 10^4,[l_i,r_i]\in [0,10^{18}]$

首先考虑如果所有 $l_i=r_i$ 怎么做，建出所有数的反 trie，一开始在根节点，每次操作就是往左儿子或右儿子走，不能走到空结点。设 $f_u$ 表示在 $u$ 时先手是否会赢，则转移为 $f_u = \overline{f_{ls}}\or \overline{f_{rs}}$。

考虑一个区间 $[l,r]$ 内的数，我们考虑将区间拆成 $[0,2^{60})$ 的线段树上的 $\log$ 个区间。对于拆出来的每个区间，可以发现这个区间内所有数建出来的反 trie 为：前 $\log(r-l+1)$ 层是一棵满二叉树，然后二叉树上每个节点后面跟了一条相同的链。于是我们维护 $60$ 个 trie 树，第 $i$ 棵 trie 树的前 $i$ 层是满二叉树，并且前 $i$ 步无论怎么走都是等价的，于是可以将前 $i$ 个点合并成一条链，下面再接一棵树。

统计答案时在 $60$ 棵 trie 树上一起跳，然后用一个记忆化搜索，那么状态数是节点数的，复杂度 $\mathcal{O}(n\log^2 V)$。具体可以看代码。

Submission #69199610 - AtCoder Grand Contest 064

[AGC064D] Red and Blue Chips

你有 $n$ 个字符串，初始情况下每个字符串只有一个字符，是 R 或 B，保证第 $n$ 个字符串是 B。

你需要对每个 $i=1,2,\cdots ,n-1$ 依次执行以下操作：

选择一个整数 $j$ 使得 $i< j\le n$，且第 $j$ 个字符串的最后一个字符是 B，然后把第 $i$ 个字符串整体拼接在第 $j$ 个字符串的前面。

问最后可以得到多少种本质不同的第 $n$ 个字符串，对 $998244353$ 取模。

考虑倒着做，一开始只有第 $n$ 个字符串有 $n$ 个字符。依次枚举 $i=n-1,n-2\ldots 1$，如果这一位初始时是 R，那么就要选择一个 $i+1\sim n$ 中开头为 R 的字符并且删掉；如果初始为 B，那么就是选择 $i+1\sim n$ 中某个含有至少 $2$ 个 B 的串，然后选择一个非末尾的 B 将这个串划分为两部分。

考虑怎么判断一个最终串 S 是否合法，设 $m$ 表示有多少个 B，$a_i$ 表示初始时从右往左第 $i$ 个 B 到左边的 B 间有多少个 R。那么一开始会删除 S 前面 $a_1$ 个 R，所以要求 S 开头至少有 $a_1$ 个 R。接着遇到一个 B 将 S 划分为两部分，相当于可以多露出一些 R，那么我们选择前面有最多 R 的 B 进行切割一定最优，然后又删去一些 R，要求剩下露出的 R 够删，遇到 B 又选择一个当前 $a_i$ 最大的 B 进行切割。

也就是说，设 $b_i$ 为 S 串中从左往右第 $i$ 个 B 到左边的 B 间有多少个 R，那么这个串合法的条件为：将 $b_2\sim b_m$ 排序，则 $\forall 1\le x\le m$，满足 $\sum\limits_{i=1}^x b_i\ge \sum\limits_{i=1}^x a_i$。接下来计数就比较简单了，依次枚举排序后 $b_1\sim b_m$ 是什么，因为要求排序前有多少种可能，所以需要枚举每个值的出现次数。设 $f_{i,j}$ 表示当前分了 $i$ 段，$b$ 的和为 $j$，然后从大到小枚举 $x$ 和 $x$ 的出现次数 $c$，要求这之间的每个前缀和都满足条件，就有转移：$f_{i+c,j+kc}\larr f_{i,j}\frac{1}{c!}$。最后答案为 $m!f_{m,n}$，复杂度为 $\sum\limits_{i=1}^n\mathcal{O}(\frac n i)^2\times \mathcal{O}(n) = \mathcal{O}(n^3)$。

Submission #69195111 - AtCoder Grand Contest 064

AGC063

[AGC063A] Mex Game

skip。Submission #69224382 - AtCoder Grand Contest 063

[AGC063B] Insert 1, 2, 3, ...

skip。Submission #69224576 - AtCoder Grand Contest 063

[AGC063C] Add Mod Operations

给定两个长度为 $n$ 的序列 $a,b$，判断能否用至多 $n$ 次操作让 $a$ 变成 $b$，操作如下：

选择两个整数满足 $0\le x < y\le 10^{18}$，将所有 $a_i$ 变为 $(a_i+x)\bmod b_i$

如果有解需要构造。$n\le 1000,0\le a_i,b_i\le 10^9$

首先有解的一个必要条件为对于所有相同 $a_i$，它们对应的 $b_i$ 也需要相同。判了这个之后我们将相同的 $a_i$ 缩起来并按 $a_i$ 排序。考虑如下操作，选择某个 $x$ 和 $y = \max\{a_i\}+x$，将所有 $a_i$ 画到数轴上，这相当于将 $a_n$ 设为 $0$ 并将其余 $a_i$ 都向又平移 $x$。我们重复以上操作 $n-1$ 次，数轴上的顺序为 $a_2,a_3\ldots a_n,a_1$，满足 $a_2=0$ 并且任意两个 $a_i$ 之间的距离都是我们可以决定的。

现在 $b_i$ 是乱序的不太好做，我们可以设一个 $inf = 3\times 10^9$，然后最后一步模 $inf$，然后将每个 $b_i$ 增加 $inf$ 直到所有 $b_i$ 按 $b_2,b_3\ldots,b_n,b_1$ 的顺序排序。那么最后一步的操作就是 $x=b_2,y=inf$，这样子 $a_2$ 会由 $0$ 变为 $b_2$。然后我们算出 $b_3-b_2,\ldots b_n-b_{n-1},b_1-b_n$，于是就可以推出我们每一步中的 $x$ 是多少了，注意要有 $b_1-b_n\ge a_1$，调大 $b_1$ 即可。

Submission #69226175 - AtCoder Grand Contest 063

[AGC063D] Many CRT

给定正整数 $n,a,b,c,d$，判断是否存在非负整数 $x$，满足 $\forall k=[0,n-1],x\equiv a+bk\pmod{c+dk}$。如果存在，求出最小的 $x$ 对 $998244353$ 取模后的结果。

$n,a,b,c,d\le 10^6$

显然直接 CRT 很难做，我们观察发现如果给 $x\equiv a+bk\pmod{c+dk}$ 左右都乘上 $d$，那么式子变为 $dx\equiv ad+bdk\pmod{c+dk}$，即 $dx\equiv ad-bc\pmod{c+dk}$，这样子余数都是固定的了！但是乘 $d$ 的前提条件是 $\gcd(d,c+dk) = 1$，即 $\gcd(c,d) = 1$。

我们假设 $\gcd(c,d) = g$，尝试对整个东西都除以 $g$。首先将 $n=0$ 和 $n=1$ 的式子相减，可以得到 $b$ 是 $g$ 的倍数，所以如果 $b\nmid g$ 就是无解。然后对于 $n=0$，有 $x\equiv a\pmod g$，于是可以先将 $x,a$ 都先除以 $g$ 向下取整。所以我们令 $a'\larr \lfloor\frac a g\rfloor,b'\larr \frac b g,c'\larr \frac c g,d'\larr \frac d g$，求出答案 $x'$ 后最终答案为 $x = x'g+(a\bmod g)$。

现在有了 $\gcd(c,d) = 1$，令 $u=ad-bc$，于是乘 $d$ 后式子变成了 $dx\equiv u\pmod{c+dk}$。令 $L=\operatorname{lcm}\{c+dk\}$，相当于求一个 $x$ 满足 $dx\equiv u\pmod L$，因为 $d$ 与 $L$ 互质，所以这个式子一定有解。也就是说无解的充要条件是 $b\nmid g$。接下来考虑求解 $x$ 的最小值，因为 $dx\equiv u\pmod L$，所以我们令 $dx = u+Ly$，我们要求出最小的 $y$ 满足 $d|u+Ly$。于是考虑求出 $y_0 = y\bmod d$ 的值，那么所有 $y$ 都可以写作 $y_0+td$。

我们将 $dx = u+Ly$ 两边 $\bmod d$，可以得到 $0\equiv u+Ly\pmod d$，即 $\frac{-u}{L}\equiv y\pmod d$，相当于求出 $L$ 与 $d$ 的逆元即可（这个逆元一定存在），即求出 $L\bmod d$，也就是说我们要求 $L$ 的质因数分解，这个在下面提到。知道了 $y_0 = y\bmod d$ 之后，将 $y$ 写成 $y_0+td$，于是 $x = \frac{u+(y_0+td)L}d$，现在要求一个最小的 $t$ 满足 $u+(y_0+td)L$ 是正数，我们分类讨论：

如果 $|u|\ge L$，那么暴力求即可。
否则就是 $L$ 特别大的一般情况，此时如果 $u<0$ 且 $y_0=0$，那么 $t=1$，否则就是 $t=0$。算出 $L\bmod 998244353$ 即可。

最后考虑怎么求 $L$ 的质因数分解。我们设 $a_i = c+di$，有 $a_i\le 10^{12}$，然后枚举 $1\sim 10^6$ 内的所有质数 $p$，每次找到 $p|c+di$ 的最小的 $i$（如果 $p|d$ 就不管），然后每次 $i$ 加上 $p$，就可以找到所有是 $p$ 的倍数的 $a_i$，并将这些 $a_i$ 一直除以 $p$ 直到不能除，就能找到 $L$ 中 $p$ 的次数。枚举完之后如果剩下的所有 $a_i\ne 1$，那么一定都是互不相同的质数（假设有相同的那么相当于 $d(i-j)$ 是一个质数，不合法），再将 $L$ 依次乘上这些质数即可。那么复杂度是每个数的质因子个数之和，上界为 $\mathcal{O}(n\log n)$。

[AGC063E] Child to Parent

给定一棵 $n$ 个点以 $1$ 为根的树，第 $i$ 个点的父亲为 $p_i$，有一个数列 $a$ 和一个数 $r$，你可以进行一下操作任意次：

选择一个 $i$ 满足 $i > 1$ 且 $a_i > 0$，操作 $a_i\larr a_i-1,a_{p_i}\larr a_{p_i}+r$。

求能得到多少种不同的数列 $a$。对 $998244353$ 取模。

$n\le 300,a_i,r\le 10^9$

有点虚高。首先操作一定可以调整为从下往上操作，设 $d_i$ 表示点 $i$ 被操作了多少次，那么对于每个 $i$ 需要满足 $d_i\le a_i+\sum\limits_{(u,v)\in E} rd_v$。于是我们将问题转为计数有多少个满足上述条件的 $d_i$。

设 $f_u$ 表示子树 $u$ 内的答案，即有多少个 $d$ 序列，则答案为 $\prod\limits_{(1,u)\in E}f_u$。考虑怎么求 $f_u$，对于每一种儿子子树的 $d$ 序列，$c_u$ 的取值范围为 $[0,a_u+\sum rd_v]$，所以我们要求 $\sum(1+a_u+r\sum d_v)$。那么 $a_u$ 的贡献次数为 $\prod f_v$，然后我们需要知道 $v$ 子树内所有 $d$ 序列的 $d_v$ 的和是多少，设为 $g_v$。现在考虑求 $g_u$，则每一种儿子子树的 $d$ 序列的贡献为 ${a_u+r\sum d_u+1\choose 2}$，我们要求上式的和，此时又需要知道 $v$ 子树内所有 $d$ 序列的 $d_v^2$ 的和是多少。

一直这样子做下去，发现我们最多需要求到 $n$ 次方和，于是设 $f_{u,i}$ 表示 $u$ 子树内所有 $d$ 序列的 $d_u^i$ 之和是多少。那么转移为 $f_{u,i} = \sum S_i(a_u+r\sum d_v)$，其中 $S_k(n) = \sum\limits_{i=0}^n i^k$。我们预处理出 $S_{i,j}$ 表示 $S_i(x)$ 的各项系数，这个可以通过递推求出，那么转移为：

\[f_{u,i} = \sum S_i(a_u+r\sum d_v) = \sum_{j=0}^{i+1} S_{i,j}\sum(a_u+r\sum d_v)^j \\ \]

设 $g_j = \sum(a_u+r\sum d_v)^j$，$g_i$ 的转移式为：

\[g_j = \sum(a_u+r\sum d_v)^j = \sum_{k=0}^j {k\choose j}r^k a_u^{j-k}\sum(\sum d_v)^k \]

现在我们需要求出 $(\sum d_v)^k$ 之和，这个可以通过将 $f_{v,i}$ 看成 EGF 卷起来得到，然后就可以求出 $g$，进而求出 $f$。于是就可以在 $\mathcal{O}(n^3)$ 的复杂度内解决问题。

Submission #69549339 - AtCoder Grand Contest 063

[AGC063F] Simultaneous Floor

给定两个非负整数的有序数对 $(a_1,a_2),(b_1,b_2)$，定义一次操作为：

选择一个正实数 $x$，将 $(a_1,a_2)$ 变为 $(\lfloor a_1x\rfloor,\lfloor a_2x\rfloor)$。

求能否将 $(a_1,a_2)$ 变为 $(b_1,b_2)$，如果能，求出最小操作次数。

多组数据。$T\le 10^5,0\le a_1,a_2,b_1,b_2\le 10^9$

参考了官方题解，但是有一些证明是自己证的。如果证明部分有错误，请联系我更改。

前置知识：Stern–Brocot 树，以及在 Stern–Brocot 树上二分，比如 P8058 这个题。

先判掉答案为 $0$。如果 $a_1,a_2,b_1,b_2$ 中有至少一个数为 $0$，那么答案只有可能是 $-1/1/2$，这个也可以通过简单分类讨论判掉。

我们将 $(a_1,a_2),(b_1,b_2)$ 看成平面上的两个点（因为前面有特判，所以一定都在第一象限），那么一次操作可以看成：将 $(a_1,a_2)$ 变成 $(0,0),(a_1,a_2)$ 连线所在直线上的任意一个点，然后变成其左下角第一个整点。但如果正着做，$(a_1,a_2)$ 一次操作能到达的点不太好刻画，我们考虑倒着去做。

我们的大体思路为，求出哪些点能通过 $k$ 次变换到达 $(b_1,b_2)$，找到第一个 $k$ 满足这些点的集合中包含 $(a_1,a_2)$ 即为答案。

考虑哪些点能通过一次操作到达 $(b_1,b_2)$，相当于是 $(0,0),(a_1,a_2)$ 连线所在的直线，与 $(b_1,b_2)$ 右上方的边长为 $1$ 的正方形有交集，并且这个交集不能只在正方形的上边界和右边界，即不能只经过 $(b_1+1,b_2)$ 或 $(b_1,b_2+1)$。如下图所示：

hanghangniubi

于是一次能够到达 $(b_1,b_2)$ 的点的集合为 $S = \{(x,y)|\frac{b_1}{b_2+1} < \frac x y < \frac{b_1+1}{b_2}\}$，即蓝色区域内的点。

接下来考虑求出哪些点能通过两次操作到达 $(b_1,b_2)$，相当于一次操作能到达 $S$ 中的某个点。那么这些点构成的集合即为所有一次性能到达 $S$ 中的某个点的集合的并集，因为一次性能到达某个点的集合是斜率的一个区间（注意这个斜率是一般说的斜率的倒数），所以并集一定也是斜率的区间。于是这个区间的左端点为 $l = \min\limits_{(x,y)\in S} \frac{x}{y+1}$，右端点为 $r = \max\limits_{(x,y)\in S}\frac{x+1}{y}$，两次操作能到达的 $(b_1,b_2)$ 的集合为 $S = \{(x,y)|l < \frac x y < r\}$。（注意如果求区间并集只是单纯的这么算可能并集区间中间会有一些空的，但是本题点比较密集，可以感性理解为直接取左端点最小值和右端点最大值是对的）

接下来三次，四次......操作能到达的点的集合也可以类似求出。设 $l_i,r_i$ 表示 $i$ 次操作能到达 $(b_1,b_2)$ 的斜率区间为 $(l_i,r_i)$，初始时 $(l_1,r_1) = (\frac{b_1}{b_2+1},\frac{b_1+1}{b_2})$，然后递推为 $l_i = \min\limits_{l_{i-1} < \frac x y < r_{i-1}}\frac{x}{y+1},r_i = \max\limits_{l_{i-1} < \frac x y < r_{i-1}}\frac{x+1}{y}$。找到第一个 $k$ 满足 $l_k < \frac{a_1}{a_2} < r_k$ 就是答案，或者如果某次 $(l_k,r_k) = (l_{k-1},r_{k-1})$ 就是无解。

接下来考虑如何快速求 $l_k,r_k$，因为求 $l_k$ 和求 $r_k$ 是同理的，不妨考虑求 $r_k$。问题为给定两个分数 $l,r$，求 $\max\limits_{l < \frac x y < r}\frac{x+1}{y}$，显然如果确定了 $y$，$x$ 能取得越大越好。接下来，我们可以说明，当 $y$ 取到最小值（即存在至少一个 $x$ 满足限制），$x$ 再取到最大时，此时的 $\frac{x+1}y$ 就是最大值。

我们可以先找出这个 $\frac x y$ 是什么，找到 $l,r$ 在 Stern–Brocot 树上的位置，然后分类讨论一下，如下图：

pmxniubi

可以发现，如果 $y = 1$ 时没有 $x$ 满足条件，$\frac x y$ 就是从根节点不断往下走，第一次走到区间 $(l,r)$ 内的分数。并且此时一定只有一个 $x$ 满足条件，因为 $\frac x y$ 的子树内没有其他分数的分子为 $x$，所以 $\frac{x+1} y$ 一定在右边的某棵子树内，而这棵子树一定不在区间 $(l,r)$ 内，$\frac{x-1}{y}$ 同理。现在我们要证明，子树内没有其他分数 $\frac{x'}{y'}$ 满足 $\frac{x'+1}{y'} > \frac{x+1} y$，相当于证明每次从一个点往右儿子走时 $\frac{x+1}{y}$ 的值都会减小。

当一个点往右儿子走时，设这个点的分数为 $\frac{x_1}{y_1}$，右儿子的分数为 $\frac{x_1+x_2}{y_1+y_2}$，根据定义，$\frac{x_2}{y_2}$ 表示 $\frac{x_1}{y_1}$ 上方第一个向左走的分数。那么我们要证 $\frac{x_1+1}{y_1} > \frac{x_1+x_2+1}{y_1+y_2}$，即 $(x_1+1)(y_1+y_2) > (x_1+x_2+1)y_1$，$(x_1+1)y_2 > x_2y_1$，即 $\frac{x_1+1}{y_1} > \frac{x_2}{y_2}$，这个根据上面的分析，$\frac{x_1+1}{y_1}$ 一定在 $\frac{x_2}{y_2}$ 的右侧的子树内，所以是对的。如下图：

pmxnb

于是我们就证明了上面的结论，那么每次在 Stern–Brocot 树上二分，就可以快速从 $l_{k-1},r_{k-1}$ 递推到 $l_k,r_k$。接下来，暴力做上面的过程直到 $l_k < \frac{a_1}{a_2} < r_k$ 或者 $(l_k,r_k) = (l_{k-1},r_{k-1})$ 即可，我们可以说明，这个递推轮数在 $\mathcal{O}(\log n)$ 级别。

首先，递推结束时，$l$ 一定是 $\frac 1 y$，$r$ 一定是 $\frac x 1$。除去最开始有一两轮 $l$ 和 $r$ 在 Stern–Brocot 树上呈祖先关系，之后每轮都是取 $l$ 和 $r$ 的 lca $\frac x y$，然后 $l\larr \frac{x}{y+1},r\larr \frac{x+1} y$。依然是根据上面的分析，$l$ 会跳到 $\frac{x}{y}$ 左边的子树，$r$ 会跳到 $\frac x y$ 右边的子树。

因为根到 $\frac x y$ 走左儿子和右儿子的交替次数是 $\mathcal{O}(\log n)$ 的，而如果 $\frac x y$ 最后是走了很多次右儿子得到的，那么 $\frac x y$ 跳到右边子树，下一轮再取 lca 得到的 $\frac{x'}{y'}$ 就至少是 $\frac x y$ 上方的第一个走左儿子的节点（可以联系上图分析），另外一种情况同理。所以每一轮都会干掉 $\frac x y$ 最后的一段连续段，而因为交替次数是 $\mathcal{O}(\log n)$ 的，所以递推轮数也是 $\mathcal{O}(\log n)$ 的。

于是暴力递推即可，总复杂度为 $\mathcal{O}(T\log^2 n)$。

Submission #69555860 - AtCoder Grand Contest 063

AGC062

[AGC062A] Right Side Character

skip。Submission #69376673 - AtCoder Grand Contest 062

[AGC062B] Split and Insert

有一个长为 $n$ 的排列 $p$，初始时 $p_i=i$，你要进行如下操作 $m$ 次：

选择一个正整数 $k$，将序列的前 $n-k$ 项和序列的后 $k$ 项以任意顺序拼起来。

给定 $c_i$，每次操作的代价是 $k_ic_i$。给定最终的序列 $a$，判断能否经过这 $k$ 次操作使得 $p$ 变成 $a$，如果能，求出最小的总代价。

$n,k\le 100,c_i\le 10^9$

将操作倒过来，每次就是选择序列的某个子序列，然后放到序列的末尾。观察第二步到第一步时的操作，考虑第二步的序列长什么样子才合法，发现要存在一个 $k$，使得序列中 $1\sim n-k$ 的相对顺序是有序的，且 $n-k+1\sim n$ 的相对顺序也是有序的。

于是我们可以将问题划分为两个子问题，一个是只考虑数列中 $1\sim n-k$ 的数，要从第 $k$ 步到第 $2$ 步变得有序，并且代价最小，另一个子问题同理。并且两个子问题的代价可以直接相加，因为如果同一步中两个子问题都操作了的话，我们可以将两个子问题中要挪到后面的子序列一起挪，并且因为代价是 $k_ic_i$，所以可以直接相加。

设 $f_{i,l,r}$ 表示只考虑 $l\sim r$ 中的数，做了了 $i\sim k$ 步，要使得 $l\sim r$ 中的数有序的最小代价是多少。初始时 $f_{k+1,l,r}$ 的值就是看最终序列中 $l\sim r$ 是否已经排好序，如果是就是 $0$，否则就是 $\infty$。转移要么是不操作，即 $f_{i,l,r}\larr f_{i+1,l,r}$，要么是选择一个 $l\le x < r$，然后 $f_{i,l,r}\larr f_{i+1,l,x}+f_{i+1,x+1,r}+c_i(r-x)$。复杂度为 $\mathcal{O}(n^3k)$。

Submission #69378088 - AtCoder Grand Contest 062

[AGC062C] Mex of Subset Sum

给定一个长度为 $n$ 的正整数序列 $a$，设集合 $S$ 为 $a$ 中任意一个子序列（可以为空）的和构成的集合，求 $S$ 中前 $k$ 个没出现过的非负整数。

$n\le 60,k\le 1000,a_i\le 10^{15}$

首先将 $a_i$ 排序，设 $sum_i$ 表示前缀和。设 $S_i$ 表示前 $i$ 个数中，$[0,sum_i]$ 中不能被凑出的数的集合。直觉来看这个 $S_i$ 可能会呈指数级增长，但是因为 $k\le 1000$ 的限制，所以中途一旦已经确定了答案就可以直接输出。考虑求 $S_i$，分两种情况讨论：

$a_i > sum_{i-1}$，那么 $S_{i-1}\cup (sum_{i-1},a_i)$ 在之后都不能被凑出，于是如果这个集合大小 $\ge k$，我们就可以直接确定答案，否则就是 $S_i = S_{i-1}\cup (sum_{i-1},a_i)\cup(S_{i-1}+a_i)$，$S_{i-1}+a_i$ 表示 $\{x|x-a_i\in S_{i-1}\}$，因为 $|S_{i-1}\cup (sum_{i-1},a_i)| < k$，所以 $|S_i|-|S_{i-1}| < k$，即增加的数个数不超过 $k$。
$a_i\le sum_{i-1}$，那么 $S_{i-1}$ 中 $ < a_i$ 的元素在之后都不能被凑出，如果个数 $\ge k$ 我们也可以确定答案。否则就是 $S_i=\{x|(x\in (sum_{i-1},sum_i]\or x\in S_{i-1})\and (x < a_i\or x-a_i\in S_{i-1})\}$，那么 $|S_i|$ 的上界就是每个 $x\in S_{i-1}$ 在 $+a_i$ 之后都不能被凑出，再拼上所有 $S_{i-1}$ 中 $<a_i$ 的元素。而前者个数 $=S_{i-1}$，后者个数 $< k$，所以依然有 $|S_i|-|S_{i-1}| < k$。

于是每次要么可以直接求出答案，要么集合大小增加不超过 $k$，所以直接用 set 维护即可，复杂度为 $\mathcal{O}(n^2 k\log(nk))$。

Submission #69377173 - AtCoder Grand Contest 062

[AGC062D] Walk Around Neighborhood

有 $n$ 个正偶数 $D_i$，一个人初始在 $(0,0)$，每次他可以选择一个未被擦除的 $d_i$ 擦去，然后走到一个和自己曼哈顿距离为 $d_i$ 的位置。$n$ 次操作后，他必须回到原点 $(0,0)$。判断是否有解，如果有解，设他在第 $i$ 次操作后在 $(x_i,y_i)$ 位置，求出 $\max\{|x_i|+|y_i|\}$ 的最小值。

$n,D_i\le 2\times 10^5$

*本题解为加强版，加强版中 $n,D_i\le 10^6$，并且不保证 $D_i$ 是偶数。

将 $D_i$ 从小到大排序，然后为了方便思考，把曼哈顿距离转化为切比雪夫距离，每次一个点就能走到一个正方形上的点。先考虑无解条件，如果 $\sum\limits_{i=1}^{n-1}D_i < D_n$，那么一定无解，否则一定有解，且答案在 $[\frac {D_n} 2,D_n]$ 之间。

考虑证明，下限为 $\frac{D_n}2$ 是显然的，因为要走 $D_n$ 这一步。然后我们可以构造出一组答案为 $D_n$ 的解出来，因为 $\sum\limits_{i=1}^{n-1}D_i \ge D_n$，所以可以先用一些 $D_i$ 走到距离原点边长为 $D_n$ 的正方形上。接着除了最后一步 $D_n$，因为 $D_i < D_n$，所以可以一直在正方形边界上走，最后用一步 $D_n$ 回去。于是就证明了答案一定在 $[\frac {D_n} 2,D_n]$ 内，现在我们考虑如何判断一个答案是否合法。

假设当前的答案是 $r$，那么整个行走的过程都必须在距离原点半径为 $r$ 的正方形内。我们尝试找到一种最优的策略，观察发现，我们的方案一定是先从原点走一些 $D_i$ 到正方形边缘上，然后再在正方形边缘上随便走（因为 $a_i\le \frac r 2$，所以一定可以一直停在正方形边上），最后再走一些 $D_i$ 回到原点。

因为从原点走到正方形上和走回来是等价的，所以问题就是如何判断一个集合 $D_i$ 能否从原点走到正方形边上。

设 $s = \sum D_i[D_i < r]$，如果 $s\ge r$，那么一定有解。现在考虑 $s < r$ 且有 $D_i \ge r$ 时的答案，可以发现对于一个 $\ge r$ 的 $D_i$ 最多只会用一个，因为每次走的时候要么直接无法走到半径为 $r$ 的正方形内或者可以直接走到正方形边上。并且越小的 $D_i$ 用不容易走出去，所以我们只会用最小的 $\ge r$ 的 $D_i$，记为 $x$。

而对于 $<r$ 的 $D_i$，因为 $s < r$，而且在离原点越远的位置使用 $x$ 越容易有解，所以一定会先走到离原点半径为 $s$ 的正方形上，然后使用一次 $x$，于是有解的条件就是 $x-s\le r$。

现在考虑枚举答案 $r$，我们要把所有 $D_i$ 分成两部分使得两部分都满足上述条件。因为有一个 $\ge r$ 的 $D_i$ 肯定比没有好，所以我们给两部分分别选出两个最小的 $\ge r$ 的 $D_i$，如果没有就不选，这样就可以计算出两个部分 $s$ 的下界。于是问题就变成了能否将 $<D_i$ 的部分分成两个集合，使得两个集合的值都分别 $\ge$ 某个数。

根据上述条件我们发现，如果一个实数 $x$ 可以作为答案且 $x\ne \frac{D_n} 2$，那么 $\lfloor x\rfloor$ 也一定可以作为答案。所以除了 $\frac{D_n} 2$ 以外，其他答案一定是整数，于是我们可以直接枚举答案 $r$，每次将所有 $< r$ 的 $D_i$ 加入背包，然后用一次 _Find_next 即可判断。时间复杂度 $\mathcal{O}(\frac{n^2}\omega)$。（默认值域与 $n$ 同阶）

继续思考我们发现，如果当前 $<r$ 的 $D_i$ 的和已经很大了，那么一定可以将这些数分成两组使得这两组的和都 $\ge r$。具体来说，如果 $(\sum D_i[D_i < r])\ge 3r$，那么向一个集合中加入 $D_i$ 直到集合的和第一次 $\ge r$，剩下的数的和也一定 $\ge r$。

特判掉这种情况后，就只需要做 $D_i$ 和为 $\mathcal{O}(n)$ 的背包。于是 $D_i$ 最多有 $\mathcal{O}(\sqrt n)$ 种不同的值，可以使用二进制分组背包，复杂度为 $\mathcal{O}(\frac{n\sqrt n}\omega)$。

原版代码：Submission #64160986 - AtCoder Grand Contest 062

加强版代码：Submission #64383727 - AtCoder Grand Contest 062

[AGC062E] Overlap Binary Tree

给定 $n,k$，求有多少个 $(l_1,r_1,\ldots,l_n,r_n)$ 满足以下几个条件：

$(l_1,r_1,\ldots,l_n,r_n)$ 构成了 $1\sim 2n$ 的排列。

$l_1\le l_2\le \ldots\le l_n$。

$\forall1\le i\le n,l_i\le r_i$

恰好有 $k$ 个 $i$ 满足 $r_i = l_i+1$。

存在一个大小为 $n$ 的有根二叉树满足：$\forall 1\le i,j\le n$，$[l_i,r_i]\cap[l_j,r_j]\ne \empty$ 当且仅当 $i,j$ 在树上呈子孙关系。有根二叉树的定义为：每个点的要么是叶子，要么有两个儿子。

答案对 $998244353$ 取模。$n,k\le 2\times 10^5$

去掉第二个条件，最后将答案除以 $n!$。我们先不考虑第四个条件，求方案数。我们考虑将 $(l_1,r_1,\ldots,l_n,r_n)$ 唯一映射到某个有根二叉树上，首先一定恰好存在一个区间满足其和所有区间有交，我们将这个 $i$ 设为根节点并将这个区间删掉。剩下的区间一定可以划分完全不交的两部分，我们将值小那部分设为左子树，值大的设为右部分，递归下去建树即可。

接下来考虑枚举所有有根二叉树，求这棵树能对应多少个 $(l_1,r_1,\ldots,l_n,r_n)$。从下往上考虑 dp，设 $f_u$ 表示 $u$ 子树内的方案数（即最终 $l,r$ 的相对大小有多少种可能），那么 $f_u$ 就是 $f_{ls}f_{rs}$ 乘上 $[l_i,r_i]$ 有多少种取值可能。

考虑 $l_i$，我们需要 $l_i$ 小于左子树中所有区间的右端点，那么找出左子树中右端点的最小值，因为一个点子树内右端点的最小值一定在左子树内，所以右端点最小值一定这个点一直往左走走到的点上。并且，往左走的点的个数就是小于右端点最小值的值的个数，设有 $x$ 个，那么 $l_i$ 就有 $x+1$ 种插法，$r_i$ 同理。于是，设点 $i$ 往左走最多走 $a_i$ 步，向右走最多走 $b_i$ 步，那么这棵树的贡献就是 $\prod(a_i+1)(b_i+1)$。

换种考虑方式，设每个叶子节点往上不改变方向最多能走 $d_i$ 次，那么贡献就是 $\prod (d_i+1)!$。接下来就是一步非常巧妙的转化，我们对于每个非叶子节点，将这个点一直向左和向右走到的两个叶子节点间连一条边，设一共有 $m = \frac{n+1}{2}$ 个叶子节点，那么会连出来一个 $m$ 条边的树。并且每个叶子结点的 $d_i$ 就是树中点 $i$ 的度数，我们尝试将有根二叉树和新树一一对应，那么新树中就是以一条边为根节点，并且每个节点连向儿子的边有顺序。

可以发现如果知道了如上的一棵树，即以边为根且子树间有顺序，那么一定可以还原出原来的有根二叉树（称为有序树）。具体的，根节点那条边将树划分为了两部分，即原二叉树的左右两棵子树，然后对于一棵子树，新树根边的端点的第一个儿子的子树，又将这棵子树划分为了两部分。一直递归下去，即可还原整棵二叉树。于是我们计数新树即可，假设现在知道每个点的度数 $deg_i$，求有多少个有序树满足条件。

我们相当于要确定每个点第 $1\sim deg_i-1$ 个儿子是哪个点，即要填 $m-2$ 个数到这 $m$ 个数组中。我们考虑每次任意选择一个位置，然后填上任意一个之前没有被填过的数，那么会填 $m-2$ 次。第 $i$ 次可以选择的位置数有 $m-2-i+1$ 个，可以填的数有 $m-i$ 个（不能填前 $i-1$ 个和自己），于是总方案数为 $\prod\limits_{i=1}^{m-2}(m-i-1)(m-i) = (m-2)!(m-1)!$。最后还要添加一条根节点的边，因为根节点要区分左右子树，所以有 $2$ 种方案。而因为任意一个有根树，不同的填数方案都会被重复计算，所以答案要除以 $(m-2)!$，于是最终答案为 $2(m-1)!$。即对于任意一种 $deg_i$ 的方案，贡献都是 $2(m-1)!$。

于是我们可以生成函数来刻画方案，即答案为：

\[\frac 1{n!}\times {n\choose m}\times (n-m)! \times 2(m-1)!\times [x^{2m-2}](\sum_{i=1}^m (i+1)!x^i)^m \]

其中 ${n\choose m}$ 是选出 $m$ 个叶子，$(n-m)!$ 表示非叶子结点可以任意排列，前面部分化简为 $\frac 2 m$。

接下来考虑恰好有 $k$ 个 $r_i=l_i+1$，那么这些点一定都是叶子节点。如果这个点的 $deg_i=d$，上面的点就不能再插在 $(l_i,r_i)$ 中间，那么贡献就不是 $(d+1)!$ 而是 $d!$。剩下 $m-k$ 个叶子节点，就要求上面的点中至少有一个点插在 $(l_i,r_i)$ 间，贡献为 $(d+1)!-d!$，所以最终答案为：

\[{m\choose k}\frac 2 m[x^{2m-2}](\sum_{i=1}^mi!x^i)^k(\sum_{i=1}^m((i+1)!-i!)x^i)^{n-k} \]

多项式快速幂计算即可。复杂度 $\mathcal{O}(\log n)$。

Submission #69750655 - AtCoder Grand Contest 062

AGC061

[AGC061A] Long Shuffle

有一个长度为 $n$ 的序列 $a$，初始时 $a_i=i$。定义 $shuffle(l,r)$ 为：

如果 $l+1=r$，则 $swap(a_l,a_r)$。

否则，依次执行 $shuffle(l,r-1),shuffle(l+1,r)$。

多组询问，每次给定 $n,k$，求 $a$ 在执行 $shuffle(1,n)$ 之后，$a_k$ 的值是多少。

$T\le 1000,n\le 10^{18}$

可以打个表，然后发现 $n$ 为偶数都长得很好看，所有交换都只在 $2i-1,2i$ 间发生。考虑证明，我们用归纳法，首先 $n=2$ 满足，如果 $n\ge 4$，那么我们递归两层，变为 $shuffle(1,n-2),shuffle(2,n-1),shuffle(2,n-1),shuffle(3,n)$。根据归纳法，$shuffle(2,n-1)$ 只在相邻两个数之间交换，所以两次就抵消了，而剩下的 $shuffle(1,n-2),shuffle(3,n)$ 也显然都是在 $2i-1,2i$ 中交换。

所以考虑对偶数 $n$ 求出 $a_k$ 是多少，如果 $n$ 是奇数就递归一层。求 $a_k$ 是多少相当于问第 $m$ 个数对有没有发生交换，将 $n$ 个数看成 $\frac n 2$ 个数对，将 $shuffle(1,n)$ 转化为 $solve(1,\frac n 2)$，每次就是 $solve(1,x)$ 递归到 $solve(1,x-1),solve(2,x)$，然后最终到 $solve(i,i)$ 时将第 $i$ 个数对交换。考虑 $solve(1,n)$ 时第 $k$ 个数对被交换了多少次，相当于用 $n-1$ 次将 $l$ 端点从 $1$ 增加到 $k$，即 ${n-1\choose k-1}$。根据 Lucas 定理，${n\choose k}\bmod 2 = [k\& n = k]$，于是就可以 $\mathcal{O}(1)$ 判断了。

Submission #69394775 - AtCoder Grand Contest 061

[AGC061B] Summation By Construction

有一张二分图，左部点有 $n$ 个，右部点有 $n+1$ 个，你需要给 $n\times (n+1)$ 条边染 $1\sim n$ 的颜色，使得第 $i$ 种颜色出现了 $2i$ 次，且这 $2i$ 条边构成了一条简单路径。

$T,n\le 100$

相当于给 $n\times (n+1)$ 的矩阵上写数，那么每个数出现的位置，应该是先走到同一行上的某一格，然后走到同一列的某一格，一直走下去。我们可以弱化为每次向右一格，向下一格，重复 $i$ 次，如果每次都在最左上的位置这样填，发现可以填完所有 $n$ 是奇数的情况。即：
pmx

如果 $n$ 是偶数，我们可以先将 $n$ 的 $2n$ 次填上，然后考虑划分出 $\frac n 2-2$ 条长为 $n+1$ 的路径，每条路径分给两个和为 $n+1$ 的数，最后再填上 $1,2$。可以发现只有当 $n=2$ 时是无解的。

Submission #69398334 - AtCoder Grand Contest 061

[AGC061C] First Come First Serve

有 $n$ 个人会光顾某家店，他们会在 $a_i$ 时刻进入并在 $b_i$ 时刻离开，保证 $a_i,b_i$ 分别是递增的并且构成了 $1\sim 2n$ 的排列。每个人需要在进入或者离开时在名单上写上他的编号，求有多少种可能的编号顺序。

$n\le 5\times 10^5$

将一个编号顺序对应到一种每个人的选法上，就是从前往后枚举每个编号，然后这个人能选 $a_i$ 就选 $a_i$，否则就选 $b_i$，这样一定最优。那么计数每个人的选法，就是对于所有选择了 $b_i$ 的人，需要满足 $(a_i,b_i)$ 之间至少有一人选择，否则就不合法。

接下来考虑容斥，钦定一些人选择 $b_i$ 并且要求 $(a_i,b_i)$ 中不能有人选，每个人的贡献为 $-1$。显然所有这样的 $(a_i,b_i)$ 不能有交，并且每个人的左右端点不能同时包含在 $(a_i,b_i)$ 中，于是贡献为 $2^n\prod \frac 1 {2^{b_i-a_i}}$。设 $f_i$ 表示前 $i$ 个人的答案，每次转移时，找到 $b_j\in (a_i,b_i)$ 中最小的 $a_j$，那么所有 $b_k < a_j$ 都可以转移过来，于是就是 $f_i = f_{i-1}-\frac{f_j}{2^{b_i-a_i}}$。复杂度 $\mathcal{O}(n)$。

Submission #69395281 - AtCoder Grand Contest 061

[AGC061D] Almost Multiplication Table

给定一个 $n\times m$ 的正整数矩阵 $a$，定义两个严格递增的正整数序列 $x = (x_1\ldots x_n),y = (y_1\ldots y_n)$ 的代价为 $\max\{|a_{i,j}-x_iy_j|\}$，求最小代价，并给出构造。

$n,m\le 5,a_{i,j}\le 10^9$

神仙调整法题目。

先考虑二分答案 $d$，于是设 $l_{i,j} = \max(1,a_{i,j}-d),r_{i,j} = a_{i,j}+d$，相当于限制 $l_{i,j}\le x_iy_j\le r_{i,j}$。将 $x_i$ 都初始化为 $1$，将 $y_i$ 初始化为 $\infty$，比如 $2\times 10^9$，然后不断做如下过程：

依次枚举 $i$ 从 $1\sim n$，将 $x_i$ 设为 $\max\{x_i,x_{i-1}+1,\lceil\frac{l_{i,j}}{y_j}\rceil\}$。
依次枚举 $j$ 从 $m\sim 1$，将 $y_j$ 设为 $\min\{y_j,y_{j+1}-1,\lfloor\frac{r_{i,j}}{x_i}\rfloor\}$。

一直到满足条件或 $y_1 < 1$ 就是无解。

为什么这样子是对的？我们考虑一开始时 $x_i$ 一定小于等于任意一个满足条件的 $x_i$，$y_j$ 一定大于等于任意一个满足条件的 $y_j$。而因为每次对 $x_i,y_j$ 的赋值都是必须的，相当于每时每刻的 $x_i,y_j$ 都满足者上述条件，又因为每次如果序列 $x,y$ 不合法，都一定会做出调整。那么如果存在合法的 $x_i,y_j$，我们一定能通过这种调整法找到。

接下来考虑时间复杂度，将 $x,y$ 全部设为 $1$ 可得答案一定 $\le 10^9$，所以二分的范围为 $0\sim 10^9$。所以 $x_i\le 2\times 10^9$，因为每次调整至少会对 $x$ 中的其中一个数加一，所以至多会调整 $\mathcal{O}(nV)$ 次，然而这个复杂度不太优。我们可以不妨设 $x_n\le y_m$，因为 $x_ny_m\le 2\times 10^9$，所以 $x_i\le \sqrt{2\times 10^9}$，那么调整次数就是 $\mathcal{O}(n\sqrt V)$ 的。

于是在调整的时候我们给终止条件加上 $x_n\le y_m$，然后再设 $y_m\le x_n$ 反过来做一遍即可，总复杂度为 $\mathcal{O}(n^3\sqrt V\log V)$。

Submission #69399432 - AtCoder Grand Contest 061

[AGC061E] Increment or XOR

有一个数 $x$，你可以对其进行以下两种操作任意次：

将 $x$ 加一，代价为 $A$。

选择一个 $1\sim n$ 之间的 $i$，将 $x$ 异或 $y_i$，代价为 $c_i$。

求将 $st$ 变化为 $ed$ 的最小代价是多少，或者判断无法完成。

$n\le 8,st,ed,y_i\le 2^{40},A\le 10^5,c_i\le 10^{16}$

神仙 dp 题。

发现直接做好像特别难做，我们尝试去找性质。可以发现，每次加一的时候，都相当于是给 $x$ 末尾的一段 $1$ 去全部清 $0$。我们可以将整个操作分成几个部分，分别找出第一次向第 $1$ 位进位，第 $2$ 位... 进位的位置，将这个看成一个子问题。

考虑 dp 状态应该设什么，首先 $i$ 表示整个过程都在第 $0\sim i-1$ 位中，即没有发生过 $+1$ 对第 $i$ 位的进位，还有 $S$ 表示每个 $y_i$ 异或次数的奇偶性，然后需要起始和终止状态。起始状态肯定要有 $st$，终止状态肯定要有 $ed$，然后有可能最后操作是 $+1$，向第 $i$ 位进位了，此时会清空 $0\sim i-1$ 位，所以起点还需要考虑全 $0$ 的状态。

可以发现这样子设状态就够了，即 $f_{i,0/1,0/1,S}$ 表示整个过程都在 $0\sim i-1$ 位中，起点是 $st/0$，终点是 $ed$ 还是全 $0$，注意这个全 $0$ 是最后一次 $+1$ 向第 $i$ 位进位导致的全 $0$，异或状态为 $S$。初始化 $f_{0,p,q,S} = qA+\sum\limits_{i\in S} c_i$，向第 $0$ 位进位就是加一操作。

考虑转移，枚举 $i,p$，求 $f_{i,p,0/1,S}$ 时分两种情况考虑，即是否有只向第 $i-1$ 位进位但不向第 $i$ 位进位的操作。如果没有，那么就是直接将 $f_{i-1,p,q,S}$ 转移到某个 $f_i$ 上，分第 $i-1$ 位当前是什么数和 $q$ 还有异或状态来分情况讨论。如果有，那么我们把每次向第 $i-1$ 位进位但不向第 $i$ 位的操作都拿出来，那么每次都是从 $0\sim i-2$ 位为 $0$，第 $i-1$ 位为 $1$ 转移到同样的形式。

于是设 $g_S$，表示异或状态为 $S$，当前第 $i-1$ 位为 $1$，第 $0\sim i-2$ 位为 $0$，没有向第 $i$ 位发生过进位的最小代价。那么一个 $g_S$ 转移就是枚举一个 $T$，然后 $g_S+f_{i-1,0,q,T}$ 分第 $i-1$ 位的情况可能转移到 $f_{i,p,q,S\oplus T}$ 或 $g_{S\oplus T}$ 上，即这是个最短路的形式。所以我们每次找出最小的 $g_S$ 然后转移，就能求出所有的 $f_{i,p,0/1,S}$。

最后答案为 $f_{40,0,0,S}$，时间复杂度 $\mathcal{O}(2^{2n}\log V)$。

Submission #69406415 - AtCoder Grand Contest 061

[AGC061F] Perfect Strings

给定正整数 $n,m$，一个 01 串是好的，当且仅当串中 0 的个数是 $n$ 的倍数，1 的个数是 $m$ 的倍数。一个 01 串是完美的，当且仅当这个串是好的，且任何一个非空子串都不是好的。求有多少个 01 串是完美的。

$n,m\le 40$

设 $x_i$ 表示前 $i$ 个数中 $0$ 的个数 $\bmod n$ 的结果，$y_i$ 表示前 $i$ 个数中 $1$ 的个数 $\bmod m$ 的结果，那么串合法当且仅当 $x_n=0,y_n=0$ 且不存在两个 $0\le i<j< n$ 使得 $(x_i,y_i)=(x_j,y_j)$。把 $(x_i,y_i)$ 看成坐标，就是在一个左下角为 $(0,0)$，右上角为 $(n-1,m-1)$ 的网格上。问题就是求有多少条路径，要求从原点出发，每次向上或向右走，走过边界就从另一边回来，最后回到原点，且路径除原点外不能相交。

路径不相交，可以联想到 LGV 引理。我们发现一条路径一定有若干个出口和入口，假设我们确定了这些入口，那么对面的出口也可以确定，要使路径不相交，合法的方案一定只能是从左上到右下依次匹配一个入口和出口。

我们将入口按最左一列从上到下，最下一行从左到右依次标号，现在一共有 $n+m$ 个可能的入口，假设我们钦定了哪些位置是入口，怎么判断这是否是一种合法的选择、应该怎么求方案数？

首先要从起点出发，所以 $n,n+1$ 中必须有且只有一个入口，并且因为这是一条路径，所以设最左一列有 $x$ 个入口，最下一行有 $y$ 个入口，应该满足 $\gcd(x,y)=1$，要不然这就不是一条路径了。如果以上两个条件都满足，那么求方案数就是 LGV 引理板子了。注意最后入口对应出口并不是一一对应，而是类似 $123456$ 对应 $456123$ 这样，所以会有 $x\times y$ 个逆序对，所以求出答案后要乘上 $(-1)^{x\times y}$。

显然我们不可能暴力枚举 $2^{n+m}$ 中情况。先不考虑 $n,n+1$ 中必须有入口的限制，我们考虑用生成函数的思想，将矩阵中 $1\sim n$ 的入口到每个出口的方案数乘上一个元 $x$，$n+1\sim m$ 的入口到每个出口的方案数乘上 $y$。然后因为可能不选一个入口，所以将所有一个入口到对面的出口的方案数加上 $1$，相当于不选这个入口，即将所有 $f_{i,i}$ 加一。

此时求行列式会得出一个关于 $x,y$ 的 $n+m$ 次多项式，那么左边有 $a$ 个出口，下面有 $b$ 个出口的方案数就是 $[x^ay^b]F(x,y)$。显然求这个多项式不能暴力求行列式，于是可以考虑二维拉差，将所有 $0\le x\le n,0\le y\le m$ 的 $(x,y)$ 带进去即可。

最后再加上必须有入口的限制，就是先不让 $f_{n,n}$ 加一求一次行列式，然后再不让 $f_{n+1,n+1}$ 加一求一次行列式，两次的多项式加起来即可。

二维拉差：如果有一个 $x$ 最高为 $n$ 次，$y$ 最高为 $m$ 次的多项式 $F(x,y)$，现在已知对于所有 $0\le i\le n,0\le j\le m$ 的 $(i,j)$，有 $F(x_i,y_j)=f_{i,j}$，那么可以确定出原多项式：

\[F(x,y) = \sum_{i=0}^n\sum_{j=0}^m f_{i,j}(\prod_{p=0,p\ne i}^n \frac{x-x_p}{x_i-x_p})(\prod_{q=0,q\ne j}^m\frac{y-y_q}{y_j-y_q}) \]

时间复杂度为 $\mathcal{O}(nm(n+m)^3)$。

Submission #65144565 - AtCoder Grand Contest 061

posted @ 2025-08-28 16:39 max0810 阅读(50) 评论(2) 收藏举报

刷新页面返回顶部