网络流题目选讲

网络流题目选讲

主要是网络流建模。

网络流复杂度看起来是 \(\mathcal{O}(n^2m)\)，但是大部分情况下常数都很优秀，所以下文中复杂度都可以看成 \(\mathcal{O}(能过)\)。当然还是要知道 dinic 的复杂度为 \(\mathcal{O}(n^2m)\)，费用流的复杂度为 \(\mathcal{O}(nmf)\)。

网络流一个很大的难点就是第一步你要想到这是网络流题目，然后再想后面的建模。通常情况下，网络流能把一个看似是 NPC 的问题转化为多项式问题。然而，如果这道题目本来就是一道 NPC 问题，就一定要避免一直想网络流建模的思路，这样很有可能会浪费大量时间。

下文中连 \((f,w)\) 的边表示连一条流量为 \(f\)，费用为 \(w\) 的边。

题目打乱了顺序，要不然思考的时候只局限于一个板块不太好。

P11531 [THUPC 2025 初赛] 检查站

有一张 \(n\) 个点 \(m\) 条边的图，有 \(r\) 个分部，每个分部是一个点，每条边由一个分部管理，保证这个分部在这条边的两个端点的某一个上。你需要选择最少的分部，并标记所有被分部管理的边，使得所有从 \(1\) 到 \(n\) 的路径上都有至少一条边被管理。

\(n,m\le 5\times 10^4\)

场上因为数组开小了，集齐了 \(4\) 种评测状态。

热身题，将一个分部拆成入点和出点，两点之间连流量为 \(1\) 的边，然后对于一条原图的边 \((u,v,r)\)，连边 \((u,r_{in},\infty),(r_{out},v,\infty)\)，求这个图的最小割即可。

P9879 [EC Final 2021] Check Pattern is Good)

有一个 \(n\times m\) 的矩阵，有两种颜色 W 和 B，矩阵的一些位置颜色已经确定，剩下位置由你指定颜色，要求矩阵中 \(WB\\BW\) 和 \(BW\\WB\) 这两种 \(2\times 2\) 的连续子矩阵的数量尽可能多，并输出方案。

\(n,m\le 100\)

依然场切，但是贡献了很多发罚时。

将所有 \(i+j\) 为奇数的位置的颜色取反，那么两种矩阵就变成了全 \(W\) 或全 \(B\)，这玩意和文理分科很像，用差不多的套路即可。

然后重点在构造方案，注意并不能只是根据一条边是否满流来判断这条边是否被割掉。正确方法是从源点开始 dfs，只走还有剩余流量的边，然后看能到达哪些点，那么源点到这些点之间的边一定是没割的，汇点同理，其余边就是可以割左边可以割右边。

BZOJ4261

有一张 \(n\times m\) 的网格，有一些位置必须建设过山车，其余位置不能建设，要求过山车构成一个或多个闭合回路。过山车有以下 \(6\) 种类型：

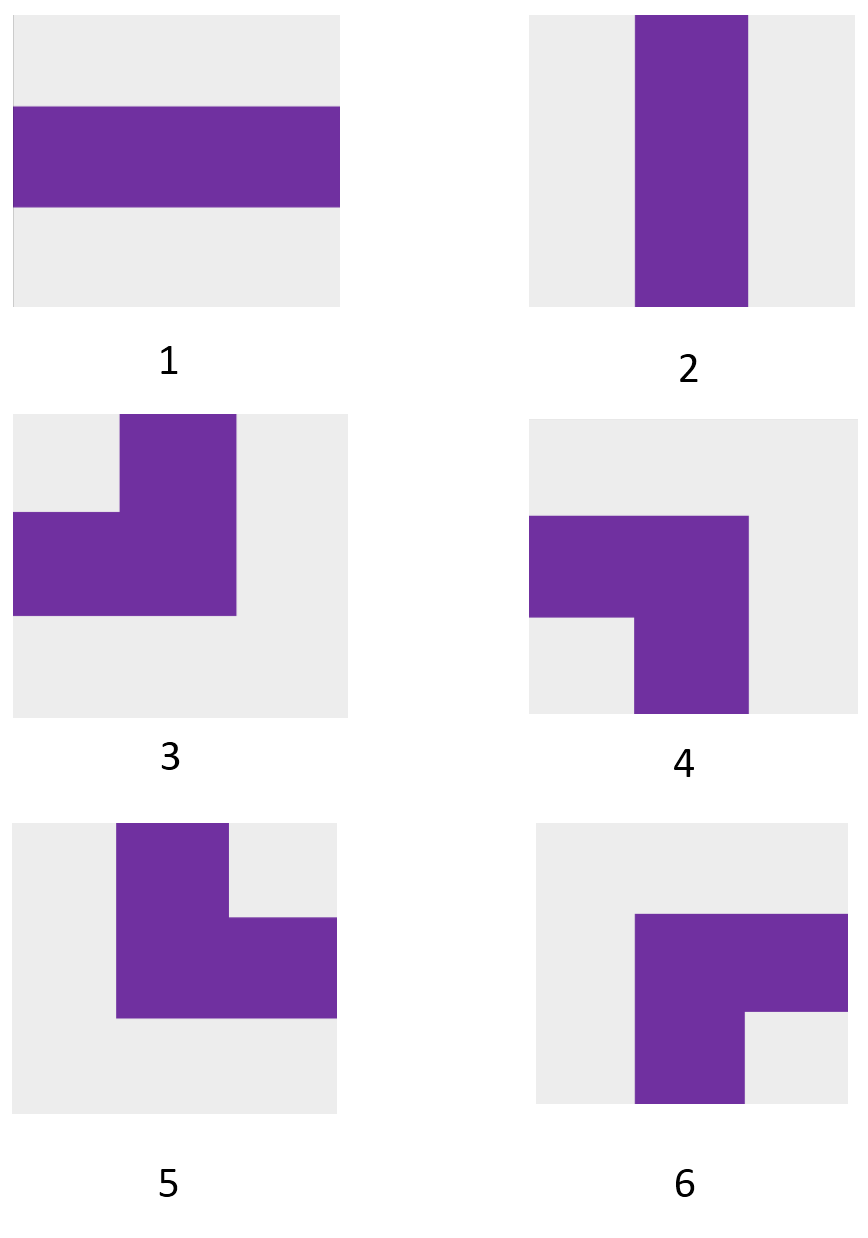
现在每个位置有一个权值 \(w_{i,j}\)，求出所有方案中弯道的权值之和最大是多少，或者报告无解。

\(n\le 150,m\le 30,0\le w_{i,j}\le 100\)

首先考虑怎么判断是否有解。考虑网络流，将网格图黑白染色，然后源点到需要放过山车的白点连流量为 \(2\) 的边，黑点到汇点连流量为 \(2\) 的边，相邻两个点间连流量为 \(1\) 的边，然后跑最大流看是否源点和汇点连的边都满流。

然后在怎么最大化弯道的权值之和，可以发现一个弯道一定是这个点横着连了一个点，竖着连了一个点。那么可以把一个点多拆出两个点，一个表示竖着连，一个表示横着连，向横着连和竖着连的两个点分别连两条重边，一条流量为 \(1\)，费用为 \(0\)，一条流量为 \(1\)，费用为 \(w_{i,j}\)。那么如果这个点是弯道，就一定会走两条费用为 \(0\) 的边，否则就会走一条费用为 \(w_{i,j}\) 的边。那么这个时候再跑最小费用最大流，然后用所有 \(w_{i,j}\) 的和减去最小费用就是答案。

提交窗口：B. 过山车（roller） - 冲刺NOI2024联测3 - 比赛 - accoders NOI

CF126E Pills

一种药片是一个 \(1\times 2\) 的矩阵，一共有 \(10\) 种药片，分别为 “BY”,“BW”,“BR”,“BB”,“RY”,“RW”,“RR”,“WY”,“WW”,“YY”。给定每种药片的数量，保证数量之和为 \(28\)，你需要把这些药片不重不漏地放入一个 \(7\times 8\) 的矩阵，使得这个矩阵和一个给定的矩阵匹配的位置数量尽量多，并构造方案。（建议看题目样例）

duel 的时候遇到了这个题，然后乱搞通过了。

如果你看到这个题一开始就往网络流方面想，比如类似上面的方法，那么恭喜你掉进坑里了。

这个题直接网络流应该是不可做的，因为这题应该是没有多项式做法的。我们考虑枚举最终每个药片的最终形态，即确定所有 |,- 的位置。然后确定位置后，就可以算出每个位置放某个类型的药片能匹配多少个位置，然后就是一个最小费用最大流的问题。然后还可以进一步优化，我们发现只用关心每个位置的两个颜色是什么，于是可以算出这 \(10\) 种类型的药片出现了多少次。

写个爆搜发现状态数在 \(10^6\) 左右，无法通过。但是可以发现如果 \(10\) 种类型药片数量都相同，那么两种划分是本质相同，于是再加个去重，状态数在 \(4000\) 左右，就可以通过了。

[AGC038F] Two Permutations

咕咕咕。

P4249 [WC2007] 剪刀石头布 - 洛谷

有 \(n\) 个人之间两两玩石头剪刀布，你知道其中一些组的输赢，你需要确定其他组的输赢，使得存在最多的无序对 \((A,B,C)\)，使得 \(A\) 赢了 \(B\)，\(B\) 赢了 \(C\)，\(C\) 赢了 \(A\)。

\(n\le 100\)

考虑如果知道两两之间的输赢如何快速统计。如果一个无序对 \((A,B,C)\) 不满足上述条件，那么充要条件是有一个人赢了其余两个人。于是我们统计出一个人 \(i\) 赢了 \(a_i\) 个人，那么答案就是 \({n\choose 3}-\sum{a_i\choose 2}\)。

可以发现 \({a_i\choose 2} = 0+1+\ldots+a_i-1\)。于是我们考虑最小费用最大流：首先源点向所有边连 \((1,0)\) 的边，然后所有边向对应的两个点连一条 \((1,0)\) 的边，留这条边表示将这个点的 \(a_i+1\)，如果一条边的胜负已经确定了，那么就只连一条边。然后所有点向汇点连 \(n\) 条边，分别为 \((1,0),(1,1),(1,2)\ldots(1,n-1)\)，因为最小费用的性质，如果一个点向汇点流了 \(x\) 的流量，那么一定走的是费用为 \(0,1,\ldots x-1\) 的边，满足上述式子。

2024.2.9 联考 T2 draw

有一幅大小为 \(n\times m\) 的画，每个位置为黑色或白色，你初始时有一个全是白色的画板，现在你需要画出这幅画。你有白色和黑色的油漆，有三个参数 \(a,b,c\) ，你可以进行如下几种操作：

• 选择一种油漆，在画板上水平或竖直地画出 \(x\) 个像素，代价为 \(ax+b\)；
• 用某个油漆在画板上画一个像素，代价为 \(c\)。

涂油漆满足后面涂的会覆盖前面的，并且有一些限制：

• 每个位置最多被油漆覆盖两次；
• 如果一个位置被涂成白色了，那么就不能再被涂成黑色了（但可以在黑色油漆上涂白色）。
• 如果一个位置目标是黑色，那么最后一定要被黑色油漆涂过；如果是白色，要么是这个位置最后被白色油漆涂过，要么是没被任何油漆涂过。

求完成目标的最小代价。\(n,m\le 40,0\le a,b,c\le 40,c\le a+b\)。

设 \(Hb_{i,j},Vb_{i,j},Hw_{i,j},Vw_{i,j}\) 表示一个位置 \((i,j)\) 是否被黑色竖着、黑色横着、白色竖着、白色横着的线覆盖过。

那么第一种操作的

代价，以黑色竖线为例，就是：\((\sum aHb_{i,j})+(\sum bHb_{i,j}\overline{Hb_{i+1,j}})\)，其余三种同理。

再对于所有黑色的格子，有代价 \(c\overline{Hb_{i,j}Vb_{i,j}}+\infty(Hw_{i,j}+Vw_{i,j})\)；对于所有白色格子，有代价 \(c(Hb_{i,j}\overline{Vw_{i,j}}+Vb_{i,j}\overline{Hw_{i,j}})+\infty Vw_{i,j}Hw_{i,j}\)，因为不可能一列同时涂黑色和白色，于是只需要考虑以上两种情况。

考虑最小割，将 \(Vb_{i,j},Hw_{i,j}\) 的意义取反，于是所有乘积就变成了 \(X\overline Y\)，的形式。于是 \(cX\overline Y\) 就是 \(Y\) 向 \(X\) 连 \(c\) 的边，\(cX\) 表示源点向 \(X\) 连 \(c\) 的边，\(c\overline X\) 表示 \(X\) 向汇点连 \(c\) 的边。

提交窗口：draw - 题目 - 🐸OJ7

[AGC031E] Snuke the Phantom Thief

在二维平面上，有 \(n\) 个珠宝，第 \(i\) 个在 \((x_i,y_i)\) 位置处，价值为 \(v_i\)。现在你可以偷走一些珠宝，有 \(m\) 条限制，每条限制为以下 \(4\) 种之一：

• 横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
• 横坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
• 纵坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
• 纵坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。

求在满足这些限制条件的情况下，偷的珠宝的最大价值和是多少。

\(n\le 80,m\le 320,x_i,y_i\le 100,0\le v_i\le 10^{15}\)。

横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗，就相当于在按横坐标排序后，编号 \(> b_i\) 的珠宝横坐标都要 \(> a_i\)。其余三个限制同理可以转化。

因为最终偷的珠宝个数不确定不太好做，我们可以枚举这个珠宝数 \(x\)，然后可以根据这些限制确定出按横坐标排序后，每个珠宝的横坐标的范围是多少，纵坐标同理，相当于把所有限制的区间取交。那么对于一个珠宝 \((x_i,y_i,v_i)\)，我们可以根据它的 \((x_i,y_i)\) 来确定它能放到横坐标的哪个区间和纵坐标的哪个区间，于是就可以考虑费用流。

处理出横坐标的 \(x\) 个区间限制和纵坐标的 \(x\) 个区间限制。源点向所有横坐标区间连 \((1,0)\) 的边，所有纵坐标区间向汇点连 \((1,0)\) 的边。然后将所有珠宝拆成左右两个点，中间连 \((1,v_i)\) 的边。然后如果一个珠宝满足某个横坐标区间的限制，那么这个横坐标区间向珠宝左边的点连边，纵坐标同理。然后跑最大费用最大流即可。

P11103 [ROI 2022] 挑战 (Day 2)

有 \(n\) 个容器和 \(m\) 个机器人，第 \(i\) 个容器最多能装 \(a_i\) 个零件，第 \(i\) 个机器人有 \(4\) 个参数 \((l_i,r_i,c_i,t_i)\)，表示机器人初始时有 \(c_i\) 个零件，它可以把零件放入编号 \(\in[l_i,r_i]\) 的容器内，并且类型为 \(t_i\)。机器人会尽可能多的把零件放入容器内。

现在你需要对于所有 \(x\in[1,n]\)，求出当所有 \(t_i=1\) 的机器人的区间变成 \([\min(l_i,x),\max(r_i,x)]\) 时，最多能将多少个零件放入容器内。每个询问间独立。

\(n,m\le 2\times 10^5,0\le a_i,c_i\le 10^9\)

这题似乎和网络流建模没有很大关系（

考虑最暴力的做法，就是对于每个 \(x\)，求出所有 \([l_i,r_i]\) 会变成什么样，然后就是一个最大流的板子。即源点向所有机器人连 \(c_i\) 的边，所有容器向汇点连 \(a_i\) 的边，所有机器人向区间内的容器连 \(\infty\) 的边，然后求最大流。

考虑优化这个过程，因为 最大流=最小割，所以我们考虑最小割的意义是什么。即选出一些机器人和容器，使得不存在任意一个区间使得机器人和容器都没选，并且代价最小。可以发现如果我们知道了要选哪些容器，那么就可以推出哪些机器人要选。于是考虑 dp，设 \(f_{i,j}\) 表示前 \(i\) 个人中，最后一个没被选的容器是 \(j\)，最小代价是多少。转移就是先令 \(\forall 1\le j < i,f_{i,j}\larr f_{i-1,j}+a_i,f_{i,i}\larr \min\limits_{1\le j < i} f_{i-1,j}\)，然后对于每个以 \(i\) 为右端点的区间 \([l,i,v]\)，执行 \(\forall l\le j\le i,f_{i,j}\larr f_{i,j}+v\)。这个 dp 显然可以线段树优化。于是就完成了 \(t_i=0\) 的问题。

然后考虑有 \(t_i=1\) 怎么做，假设当前询问是 \(x\)，那么所有 \(t_i=1\) 的区间都保护 \(x\)，于是我们可以枚举包含 \(x\) 的极长的一段被选的区间 \([l,r]\)，计算这个的代价。如果一个 \(t_i=1\) 的区间完全被 \([l,r]\) 包含，那么就不选，否则一定会选这个区间。

对于 \(t_i=0\) 的区间，可以分成几部分：完全在 \([l-1,r+1]\) 左边的区间，完全在 \([l-1,r+1]\) 右边的区间，完全被 \([l,r]\) 包含的区间，与 \([l-1,r+1]\) 相交但不被 \([l,r]\) 完全包含的区间。对于第一种情况，我们用上面的线段树优化 dp 求出 \(f_i\) 表示只考虑 \([1,i-1]\) 中的区间的最小代价，\(g_i\) 表示只考虑 \([i+1,n]\) 的区间的代价，设 \(sum_i\) 表示 \(a_i\) 的前缀和，那么一个极长段 \([l,r]\) 的代价是 \(sum_r-sum_{l-1}+f_{l-1}+g_{r+1}\)，再加上其余区间的贡献。然后发现一个区间的贡献一定二维平面上的几个矩形加，然后询问就是二维平面上的矩形求 \(\min\)，并且左端点一定是 \(1\)，于是就可以用历史最小值线段树来维护了。复杂度 \(\mathcal{O}(n\log n)\)。

CF1895G Two Characters, Two Colors

给定一个 01 串，你需要给每个节点涂上红色或是蓝色。如果你给第 \(i\) 个节点涂上红色，那么你将有 \(r_i\) 的收益，否则有 \(b_i\) 的收益。然后，你会移除所有被涂上蓝色的字符，并统计剩下字符串中的逆序对个数，并减去逆序对个数的代价。求出最大的收益减代价。

\(n\le 4\times 10^5,1\le r_i,b_i\le 10^{12}\)

考虑最小割模型，对于原串为 \(0\) 的点 \(u\)，连边 \((s,u,b_i),(u,t,r_i)\)，对于原串为 \(1\) 的点，连边 \((s,u,r_i),(u,t,b_i)\)。然后所有 \(1\) 向后面的 \(0\) 连边，然后 \(\sum r_i+b_i\) 减去最小割就是答案。

然后根据 最大流=最小割，我们可以考虑求出原图的最大流。首先每个点一定先会流 \(\min(r_i,b_i)\) 的流量，然后如果 \(b_i\ge r_i\)，那么这个点一定会涂蓝色。否则的话就只剩下一边的 \(r_i-b_i\) 的流量。然后从后往前扫，那么遇到一个 \(1\)，一定是想匹配后面尽量多的 \(0\)。相当于我们要维护一个集合，每次遇到 \(0\) 就是插入 \(r_i-b_i\)，遇到 \(1\) 就是将集合种前 \(r_i-b_i\) 大的元素 \(-1\)，并删除所有 \(0\)。

于是我们维护一个平衡树，支持插入元素，前 \(k\) 大 \(-1\)，删除 \(0\)，第二种操作就相当于分裂出平衡树中前 \(k\) 大的子树，然后打上标记。然后可能会有两个子树有相同元素的情况，但可以发现最多只有一个数会发生重复，特判一下即可。删除 \(0\) 操作也是简单的。复杂度 \(\mathcal{O}(n\log n)\)

CF1408H Rainbow Triples

给定一个长度为 \(n\) 的序列 \(p\)，你需要选出尽量多的三元组 \((a_i,b_i,c_i)\)，满足以下条件：

• \(1\le a_i < b_i < c_i\le n\)
• \(p_{a_i} = p_{c_i} = 0,p_{b_i}\ne 0\)
• 所有 \(p_{b_i}\) 互不相同
• 所有 \(a_i,b_i,c_i\) 互不相同。

\(n\le 5\times 10^5\)

设 \(0\) 的个数为 \(z\)，那么答案的上界为 \(\lfloor\frac z 2\rfloor\)，也就是说如果一个数左边有 \(\ge\lfloor\frac z 2\rfloor\) 个 \(0\)，那么这个数左边一定是可以选出 \(0\) 的，右边有 \(\ge\lfloor\frac z 2\rfloor\) 个 \(0\) 同理。然后可以发现所有位置都至少满足上述两个条件中的一个，于是我们可以把前 \(\lfloor\frac z 2\rfloor\) 个 \(0\) 划分为 \(L\) 集合，后 \(\lfloor\frac z 2\rfloor\) 个 \(0\) 划分为 \(R\) 集合。那么如果一个 \(b_i\) 是在 \(L\) 集合里面，那么只用考虑左边的 \(0\) 选啥，不用管右边，否则的话就只用考虑右边的 \(0\) 选啥。相当于我们把问题弱化为了两边只有一边需要选 \(0\)（如果两边 \(0\) 都 \(\ge \lfloor\frac z 2\rfloor\) 则直接答案加一），可以证明，所有弱化版问题中答案 \(\le \lfloor\frac z 2\rfloor\) 都一定对应一组原问题的答案，于是我们求出弱化版问题后对 \(\lfloor\frac z 2\rfloor\) 取 \(\min\) 即可。

接下来考虑弱化版怎么做，我们将一个 \(p_{b_i}\) 看成一种颜色，那么对于同一种颜色，我们只需要考虑这种颜色在 \(L\) 集合中最右边的出现位置和 \(R\) 集合中最左边的出现位置，这两个位置一定最优。于是就可以建出最大流模型，源点向所有颜色连 \(1\) 的边，每个颜色向 \(L\) 集合最右边出现位置的上一个 \(0\) 连边，向 \(R\) 集合最左边出现位置的下一个 \(0\) 连边（没有就设为 \(0\) 或 \(n+1\)），然后 \(L\) 集合中每个 \(0\) 向前面的 \(0\) 连 \(\infty\) 的边，\(R\) 集合中每个 \(0\) 向后面的 \(0\) 连 \(\infty\) 的边，每个 \(0\) 向汇点连 \(1\) 的边。

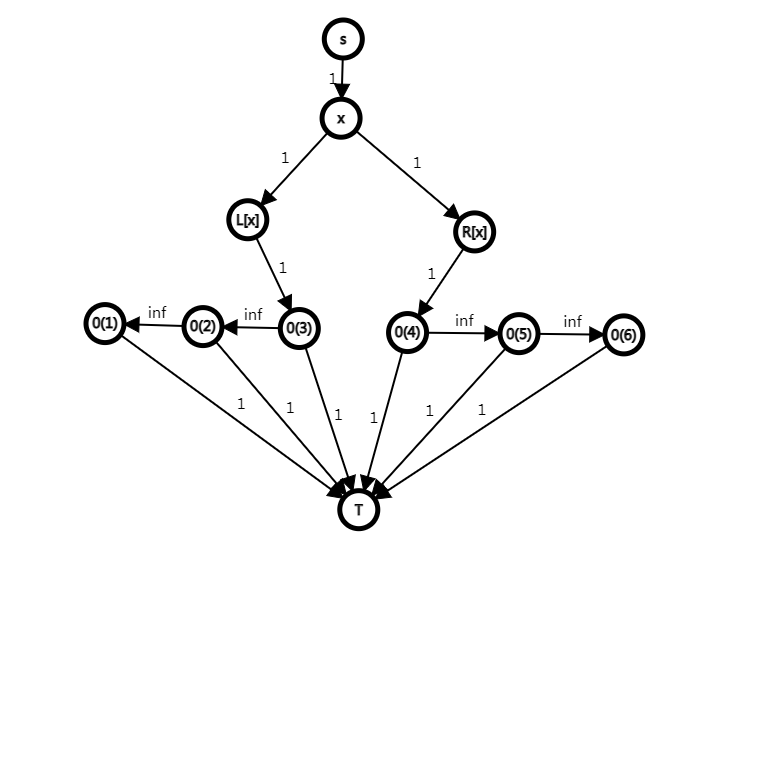
然后还是考虑 最大流=最小割，观察原图，保留源点到某个颜色的边就相当于要切掉一段前缀和后缀的 \(0\) 连向汇点的边。那么最终所有 \(0\) 割掉的边一定是一段前缀加上一段后缀，于是我们设 \(f_{i,j}\) 表示割掉前 \(i\) 个 \(0\) 和后 \(j\) 个 \(0\) 还有多少颜色需要割，于是贡献就是 \(i+j+f_{i,j}\)。于是我们可以扫 \(i\)，然后线段树维护 \(f_{i,j}\)，那么就是区间加，区间求 \(\min\)。复杂度 \(\mathcal{O}(n\log n)\)。

P4003 无限之环

有一个 \(n\times m\) 的矩阵，一共有 \(16\) 种水管，即上下左右有/无接头共 \(2^4=16\) 种。给定每个位置初始时的水管形状，定义一次操作为选择一个非直线的水管并选择一个方向旋转 \(90^\circ\)。求出最小的操作次数使得所有水管构成一些闭合回路。

\(nm\le 2000\)

先考虑怎么判断是否构成一些闭合回路，发现就是将网格黑白染色，然后源点向所有白点连一个点度数的流量，然后黑点向汇点连这个点度数的流量，相邻两个点之间如果都有接口就连边，然后看是否满流。

接下来考虑旋转会发生什么，假设只有一个点只有一个接口，旋转后相当于把原本流向这个接口的流量流向另一个接口，并且有代价，相当于一个“引流”。于是可以考虑费用流。分 \(5\) 种情况讨论。

一个可以秒的题：P3965 [TJOI2013] 循环格

[ARC122F] Domination

给定二维平面上的 \(n\) 个红点和 \(m\) 个蓝点，要求移动蓝点，使每个红点的右上方都至少有 \(k\) 个蓝点。将位于 \((x_1,y_1)\) 的蓝点，移动到 \((x_2,y_2)\) 的代价为 \(|x_1-x_2|+|y_1-y_2|\)，求最小代价。

\(n,m\le 10^5,k\le 10\)

首先一个红点如果在另一个点的左下方，那么这个点就没有用，可以去除这些点。此时剩下的红点满足 \(x\) 递增，\(y\) 递减。

我们将一个蓝点 \((bx_j,by_j)\) 移动到某个位置，那么这个蓝点能覆盖的红点一定是一段区间，区间左端点为最小的 \(i\) 满足 \(ry_i\le by_j\)，右端点为最大的 \(i\) 满足 \(rx_i\le bx_j\)，我们发现 \(x,y\) 轴时独立的。

先考虑 \(k=1\) 怎么做。我们用最短路的思想，一个蓝点覆盖如果一个区间 \([l,r]\)，那么就相当于第 \(l\) 个红点向蓝点连边，然后蓝边向第 \(r+1\) 个红点连边，两条边权和为移动的代价。然后求第一个红点到第 \(n+1\) 个红点的最短路长度。

于是我们就得出了建边方式：第 \(i\) 个红点向第 \(j\) 个蓝点连边 \(\max(0,ry_i-by_j)\)，第 \(j\) 个蓝点向第 \(i+1\) 个红点连边 \(\max(0,rx_i-bx_j)\)，然后跑最短路即可。因为边有 \(\mathcal{O}(nm)\) 条，于是我们可以用前后缀优化建图将边数优化到 \(\mathcal{O}(n+m)\)。

现在要求每个红点右上方必须有 \(k\) 个蓝点，于是可以考虑费用流，将每个蓝点拆成入点和出点，这两个点之间连流量 \(1\)，费用 \(0\) 的。其余最短路的边流量无限，费用就是边权，然后从起始点流 \(k\) 的流量的最小费用就是答案。剩下的就是费用流板子了，我们发现边权非负，所以可以跑 dijkstra 费用流，时间复杂度为 \(\mathcal{O}(k(n+m)\log(n+m))\)。

dijkstra 费用流：每次跑费用流时，因为要求最短路，而边权有可能非负，所以可以向 Johnson 求最短路一样给每个点赋一个势能 \(h_u\)，然后 \((u,v)\) 的边的边权就是 \(h_u+w_{u,v}-h_v\)。因为每次跑最短路都要求边权非负，所以每次跑完最短路都让 \(h_u += dis_u\) 即可。可以证明每次的边权都非负。其余东西和费用流一样。

CF1861F Four Suits

有 \(n\) 个人，\(4\) 种牌，初始第 \(i\) 个人有 \(a_{i,j}\) 张第 \(j\) 种牌。你是局外人，手里第 \(j\) 种卡牌有 \(b_j\) 个，你现在要把你的卡牌分给这 \(n\) 个人，使得分完之后每个人手里的卡牌总数相等，保证有解。

第 \(i\) 个人最终的分数是手里每种卡牌的数量的最大值。分数最高的那个人如果分数为 \(x\)，除了他之外分数最高的人的分数为 \(y\)，那么他会获得 \(x−y\) 的喜悦程度（显然如果存在两个分数最高的，那么他们的喜悦度都是 \(0\)），其他人会获得 \(0\) 的喜悦程度。

对于每个人，算出他最大的可能的喜悦程度。\(n\le 5\times 10^4,0\le a_{i,j},b_j\le 10^6\)。

设 \(c_i\) 表示第 \(i\) 个人会拿到多少张牌。

假设现在计算第 \(k\) 个人的答案，枚举最终成为最大值的是 \(a_{j,k}\)，要让 \(a_{j,k}\) 最大，那么 \(a_{j,k}\) 会分到 \(\min(b_j,c_i)\) 张牌。然后要让其他人的最大值尽量小，这个可以二分答案。假设现在二分的是 \(mid\)，相当于其余人的 \(a_{i,j}\) 最终都要 \(\le mid\)，然后考虑怎么判断是否可行。

考虑网络流，源点到 \(4\) 种卡牌连 \(b_j\) 的流量（\(b_j\) 要先减去 \(a_{k,j}\) 拿的牌），然后对于所有 \(i\ne k\)，每种卡牌向第 \(i\) 个人连 \(mid-a_{i,j}\) 的流量（如果 \(mid < a-{i,j}\) 那么直接不合法），每个人向汇点连 \(c_i\) 的流量。跑最大流看流量是否为 \(\sum\limits_{i\ne k} c_i\)。

然后优化，因为 最大流=最小割，转化为最小割考虑。考虑枚举割掉了哪些源点连向卡牌的边，我们假设割掉了源点连向 \(S\) 集合内的卡牌的边，那么代价就是 \((\sum\limits_{x\in S} b_x)+\sum\limits_{i\ne k}\min(c_i,\sum\limits_{x\notin S}mid-a_{i,x})\)。前面是好算的，后面部分可以先预处理出 \(c_i+\sum\limits_{x\notin S}a_{i,x}\) 排序后的结果，那么 \(\min\) 在一段前缀取到后者，可以二分。总时间复杂度为 \(\mathcal{O}(4n2^4\log n\log V)\)。

CF1178H Stock Exchange

股票交易所里有 \(2n\) 种股票，每种股票有两个属性 \(a_i,b_i\)，在时刻 \(t\ge0\)，第 \(i\) 种股票的价格为 \(a_i\times\lfloor t\rfloor+b_i\)。

每个时刻可以进行任意次股票交易，在时刻 \(t\) 时能够把股票 \(i\) 换成股票 \(j\) 当且仅当股票 \(i\) 在时刻 \(t\) 的价格不小于股票 \(j\) 在时刻 \(t\) 的价格。

现在你手上有 \(1\) 到 \(n\) 号股票各一张，现在要求的是把这些股票换成 \(n+1\) 到 \(2n\) 号股票各一张的最早时刻，以及在最早换完股票前提下的最少交易次数。

\(n\le2200,0\le a_i,b_i\le10^9\)，空间限制 16MB

首先考虑第一问，发现可以二分答案，假设现在检查时间 \(t\) 是否合法，我们发现所有的交易操作一定可以只需要在 \(0\) 或 \(t\) 内完成。于是有个贪心思路为在 \(0\) 时刻，所有股票换到能到达的股票中 \(t\) 时刻价格最大的股票，再检查 \(t\) 时刻所有股票能否交易到 \(n+1\sim 2n\)。

接下来考虑怎么最小化交易次数，我们可以将每个邮票拆成两个点，分别表示 \(0\) 时刻和 \(t\) 时刻，然后所有股票 \(0\) 时刻间连能交易的股票，费用为 \(1\)，\(t\) 时刻同理。然后跑最小费用最大流，但这样边数是 \(\mathcal{O}(n^2)\) 级别，无法通过。

对于 \(0\) 时刻，我们按所有股票按价格排序，那么一个股票连的边就是一段前缀，于是可以使用前缀和优化建图，\(t\) 时刻同理，这样就把边数缩减到了 \(\mathcal{O}(n)\) 级别。

CF1383F Special Edges

给定一个 \(n\) 个点，\(m\) 条边的有向图，每条边有边权 \(w_i\)，其中有 \(k\) 条边是特殊边。有 \(q\) 次询问，每次给定 \(k\) 个数，表示给这 \(k\) 条边赋上对应的边权，然后求原图的最大流是多少。

\(n,m\le 10^4,k\le 10,q\le 2\times 10^5\)

因为 最大流=最小割，于是考虑求出原图的最小割。对于每次询问，我们可以枚举这 \(k\) 条边中那些会被割掉，哪些不能被割掉。

相当于我们把一个集合内的边的边权设为 \(0\)，其余设为 \(25\)，然后求一次最小割，即最大流。这样子我们相当于做了 \(2^k\) 次最大流，复杂度不太能接受。

因为这些图只有很少的边不同，所以我们可以求出某个图的最大流后，更改一些边来求出新图的最大流。可以考虑用格雷码的顺序来求出每个集合的答案，这样子每次就是在原图中加一条边或删一条边然后再求答案。

思考：怎么在网络流中删边？

一些练习：水管工 - 题目 - 🐸OJ7

总结

如果你看到一个题目满足数据范围比较小，不太能做指数级算法，并且第一想法是贪心但是贪心是假的，这个时候你就可以思考网络流了。网络流主要分为建模和求解，建模部分大部分是总结经验，然后根据题目限制灵活调整，同时也要牢记各种模型，比如黑白染色，最小割模型，最大权闭合子图之类的，主要还是多刷题。

求解网络流部分如果数据规模较小就用网络流的板子（板子一定要比较优秀），否则就考虑模拟网络流，如果是最大流一般先根据 最大流=最小割 转化，然后再用数据结构来维护（一般是线段树或平衡树），模拟费用流同理。

总的来说网络流用起来非常灵活，是 OI 中一个比较神奇的工具，希望大家能熟练运用。