2025春季-好题选讲
批题乱讲
主要是一些机房内部好题选讲,八校的好题选讲,自己做的题。大部分是 AGC 中的妙妙题。
[AGC057D] Sum Avoidance
给定一个数 \(S\),称一个正整数集合 \(A\) 是好的,当且仅当 \(A\) 满足每个数都在 \([1,S)\) 内,且不能通过 \(A\) 中的数凑出 \(S\)。考虑在 \(A\) 元素最多的前提下字典序最小的 \(A\),求集合 \(A\) 中第 \(k\) 小的数是多少,或报告不存在。
多组询问。\(T\le 1000,S\le 10^{18}\)
引理 1:\(|A| = \lfloor\frac{S-1} 2\rfloor\)。
证明:我们考虑任何一对 \((i,S-i)\),这两个数中最多只有一个数会被选,如果 \(S\) 是偶数,那么还有 \(\frac S 2\) 不能选。于是 \(A\) 有一个上界 \(\lfloor\frac{S-1} 2\rfloor\)。然后如果我们选择 \(\lfloor\frac{S-1} 2\rfloor+1\sim S\) 中的所有数,这显然是一个合法的集合。于是我们就证明了 \(A\) 的上界,并且构造出了一组合法解。
所以 ,最终的答案集合中,一定是每对 \((i,S-i)\) 中恰好有一个数出现在集合中。现在,我们设集合 \(B\) 为最终的答案集合,\(A = \{x|x\in B,x\le \lfloor\frac{S-1} 2\rfloor\}\),那么我们可以通过集合 \(A\) 来推出 \(B\)。
引理 2:若集合 \(A\) 中的一些数相加能得到 \(x\),且 \(x\le \lfloor\frac{S-1} 2\rfloor\),则 \(x\in A\)。
证明:假设 \(x\notin A\),则 \(S-x\in B\),因为 \(A\) 中的数可以凑出 \(x\),又有一个数 \(S-x\),那么就能凑出 \(S\) 了,所以 \(x\) 必须在集合 \(A\) 中。
引理 3:若 \(A\) 中的数不能凑出 \(S\),那么 \(B\) 一定也不能凑出 \(S\)。
证明:假设 \(A\) 中的数不能凑出 \(S\),\(B\) 中的数能凑出 \(S\),那么这些凑出 \(S\) 的数中一定有一个是 \(> \lfloor\frac{S-1} 2\rfloor\),假设为 \(x\),这就意味着还存在一些数能凑出 \(S-x\),但是根据引理 2,\(S-x\le \lfloor\frac{S-1} 2\rfloor\),应该要加入集合 \(A\),矛盾。
根据引理 3,我们只需要求出集合 \(A\) 的最小字典序,就等同于求出了答案 \(B\)。这样有个好处就是 \(A\) 没有大小的限制,所以要求字典序最小,策略一定是从小到大看每个数能不能加入集合 \(A\),能加就加。考虑第一个应该加入的数是什么,假设这个数为 \(d\),根据上面的策略,显然就是第一个不是 \(S\) 的因数的数。根据直觉,这个数应该不会太大,实际上当 \(S\le10^{18}\) 时,\(d\le 43\)。
接下来我们把加入的数分为两类,第一类是能被 \(A\) 的数表示出来,第二类是加入了这个数后剩下的数仍然不能凑出 \(S\),应该贪心加入。从 \(\bmod d\) 的剩余系角度考虑,如果一个数是以第二类加入的,那么这个数一定和之前的数都不同余,所以以第二类加入的数不超过 \(d\) 个。于是我们可以求出 \(\bmod d\) 的同余最短路。
我们设 \(f_i\) 表示能凑出的最小的 \(\bmod d=i\) 的数,第一类情况加入的数不会对数组产生影响,于是只需要考虑第二类数是哪些,我们每次找出下一个最小的以第二类加入的数。考虑一个 \(v\) 能以第二类数加入的条件,设 \(x=v\bmod d\),首先应该有 \(v < f_{x}\),其次就是在更新完整个数组后应该满足 \(f_{S\bmod d} > S\)。
如果加入了一个 \(v\),那么最多会使用 \(d-1\) 个 \(v\) 来更新数组,因为 \(d\) 个 \(v\) 可以用 \(v\) 个 \(d\) 来代替。所以有更新:\(f_{(u+ix)\bmod d}\larr f_u+iv\),因为要让 \(f_{S\bmod d} > S\),有 \(f_{(S-ix)\bmod d} > S-iv\),即 \(v > \lfloor\frac{f_{(S-ix)\bmod d}} i\rfloor\)。于是我们能求出所有 \(\bmod d = x\) 的数中最小的能以第二类数加入的 \(v\) 是多少,即 \(v_x = \max\limits_{0\le i < d}\lfloor\frac{f_{(S-ix)\bmod d}} i\rfloor+1\)。那么这一次应该加入的数就是 \(\min v_x\)。
重复 \(d\) 次上述操作,即可确定最终的 \(f\)。然后要求出第 \(k\) 小的数,可以二分答案,求出一个 \(x\) 的排名,然后看与 \(k\) 的大小关系进行二分即可,最终时间复杂度 \(\mathcal{O}(T(d^3+d\log V))\)。
[AGC023D] Go Home
一条街上有 \(n\) 栋楼,位置分别为 \(X_1,X_2,\ldots,X_n\),第 \(i\) 栋楼里住着 \(p_i\) 个人。
初始所有人都在 \(S\) 处的一辆车上。车是自动驾驶的,对于每一时刻,还在车上的员工都会进行投票,只能投正或负方向。班车会自动统计两个方向的票数,并且往票多的方向行驶一个单位长度,如果票一样多,那就往负方向行驶。员工们也有投票策略,每一个员工都会投能让他回家时间尽量早的方向,如果两个方向一样早,那就投负方向。如果班车到达了某一个楼,那么住在那栋楼中的所有员工都会下车。
可以证明,在上述条件下,每个员工投票的方向是能够唯一确定的,班车的运行路线也能够唯一确定。询问最后一名员工回到家,经过了多少个单位时间。\(n\le 10^5\)
假设 \(X_1 < S < X_n\),现在只考虑第 \(1\) 和 \(n\) 栋楼。我们不妨设 \(p_1<p_n\)。那么这个时候班车一定会先去第 \(n\) 栋楼,最后才会去前往第 \(1\) 栋楼。证明可以考虑反证,如果先前往 \(1\),那么在最后一步时,只有 \(p_1\) 个人会投负方向,而其余人数一定 \(>p_1\)。所以会投正方向,矛盾。
于是整个班车一定是先走到 \(X_n\)(不一定一直向右),然后再一路向左走到 \(p_1\)。所以答案就是班车到 \(X_n\) 的时间加上 \(X_n-X_1\)。
我们发现,因为第 \(1\) 栋楼里的人知道自己到达的时间一定是班车到 \(X_n\) 的时间加上 \(X_n-X_1\),所以他们的目标就变成了尽量让班车更快到 \(X_n\),这个目标和第 \(n\) 栋楼里的人的目标相同!于是我们可以直接将第 \(1\) 栋里的人合并到第 \(n\) 栋里,然后变成一个 \(n-1\) 的子问题。
于是可以直接递归下去,直到 \(S \le X_1\) 或 \(S\ge X_n\),这个时候可以直接计算。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 1e5+5;
int n,s;ll x[N],p[N];
ll solve(int l,int r,bool tp)
{
if(s <= x[l])return x[r]-s;
if(x[r] <= s)return s-x[l];
if(p[l] < p[r])return p[r] += p[l],solve(l+1,r,1)+!tp*(x[r]-x[l]);
return p[l] += p[r],solve(l,r-1,0)+tp*(x[r]-x[l]);
}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();s = rd();
for(int i = 1;i <= n;i++)x[i] = rd(),p[i] = rd();
cout << solve(1,n,p[1] < p[n]?0:1) << endl;
return 0;
}
\(tp=0\) 表示最后有一次从左一直到最右的班车,\(tp=1\) 表示最后有一次从右一直到最左的班车。
[AGC048D] Pocky Game
有 \(n\) 堆石子排成一排,第 \(i\) 堆有 \(a_i\) 个,有两个人在上面玩游戏。每次先手在最左端的石子中拿至少一个(至多拿完),然后后手在最右端的石子中拿至少一个(至多拿完)。无法操作的人失败,求先手必胜还是后手必胜。
\(T,n\le 100,a_i\le 10^9\)
对于一堆石子,假设除了第一堆外的石子数量都是固定的,那么对于先手,第一堆的石子数量一定是越多越好,因为少的石子第一步能达到的状态多的石子肯定也能达到。所以一定有一个分界点,满足第一堆石子数量如果少于就必败,否则就必胜。
于是我们可以用 \(f_{l,r}\) 表示在区间 \([l,r]\) 中,固定了\([l+1,r]\) 的数量,\(a_l\) 最小是多少时,先手必胜。\(g_{l,r}\) 表示固定了 \([l,r-1]\) 的石子数量, \(a_r\) 最小是多少,后手必胜(假设这里后手先操作)。初始化有 \(f_{i,i} = g_{i,i} = 1\)。
考虑求 \(f_{l,r}\),首先如果有 \(a_r < g_{l+1,r}\),那么先手可以直接取完第一堆石子,则 \(f_{l,r} = 1\)。否则,先手肯定只会取一个石子(因为第一堆石子越多越好),我们让 \(a_l--\)。这个时候该后手操作,如果 \(a_l < f_{l,r-1}\),那么后手将这一堆石子取完就必胜,否则后手也只会取一个石子。于是双方就是每次都取一个石子,直到 \(a_l < f_{l,r-1}\) 或 \(a_r < g_{l+1,r}\)。
所以先手必胜的条件就是 \(a_l-f_{l,r-1} > a_r-g_{l+1,r}\),所以我们可以求出 \(f_{l,r} = a_r-g_{l+1,r}+f_{l,r-1}+1\)。\(g_{l,r}\) 的转移同理。
于是我们就可以在 \(\mathcal{O}(n^2)\) 的时间内求出所有 \(f,g\),最后先手必胜的条件就是 \(a_1\ge f_{1,n}\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 105;
int a[N],n;ll f[N][N],g[N][N];
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
for(int t = rd();t--;)
{
n = rd();
for(int i = 1;i <= n;i++)a[i] = rd(),f[i][i] = g[i][i] = 1;
for(int l = 1;l < n;l++)for(int i = 1;i+l <= n;i++)
{
int j= i+l;
f[i][j] = a[j] < g[i+1][j]?1:f[i][j-1]-g[i+1][j]+a[j]+1;
g[i][j] = a[i] < f[i][j-1]?1:g[i+1][j]-f[i][j-1]+a[i]+1;
}
puts(a[1] >= f[1][n]?"First":"Second");
}
return 0;
}
[AGC067D] Unique Matching
定义 \(n\) 个区间 \([l_i,r_i]\) 是好的当且仅当存在唯一一个排列 \(p\) 使得 \(\forall 1\le i\le n,p_i\le[l_i,r_i]\)。给定 \(n\) 和质数 \(p\),求有多少组 \(n\) 个区间是好的。
\(n\le 5000\)
首先如果一组区间对应的排列不是 \(p_i=i\) 的排列,那么可以交换其中的某些区间来让 \(p_i=i\),于是只需要求出对应 \(p_i=i\) 的排列的方案数,最后乘上 \(n!\)。
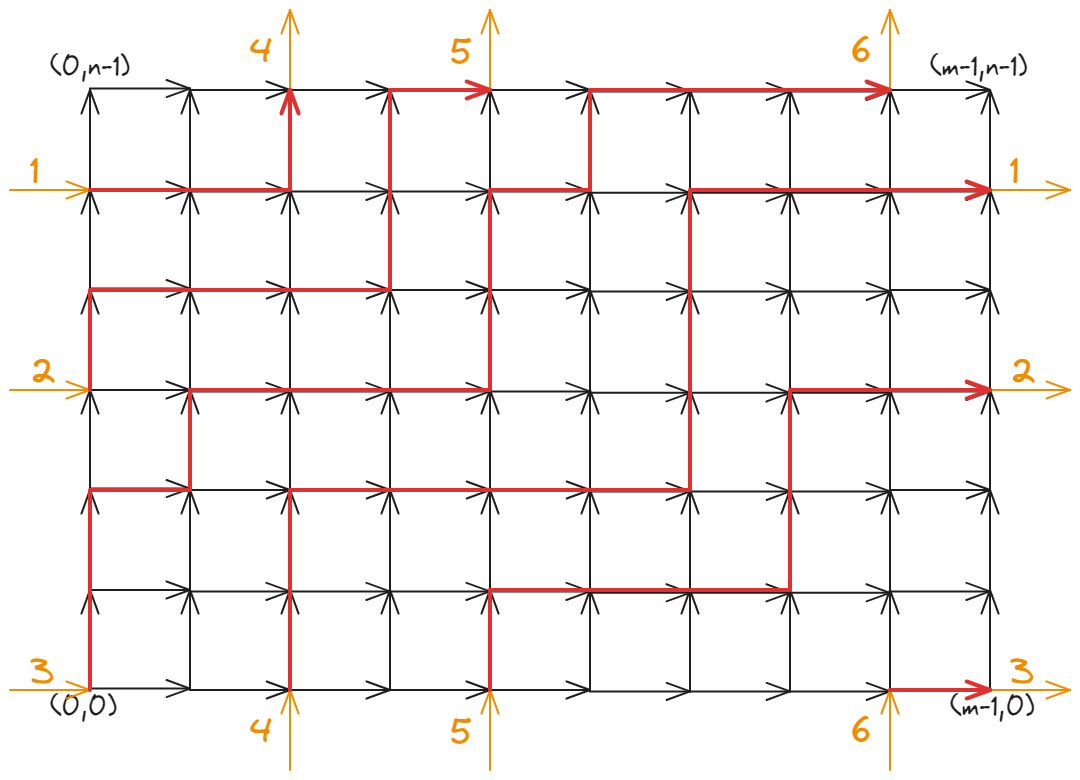
然后考虑什么样的一个区间组是合法的。如果存在 \(i,j\) 满足 \(i\in [l_j,r_j],j\in[l_i,r_i]\),那么可以交换 \(i,j\),于是这个方案就不合法。进一步可以通过归纳法得出,一个区间组合法,当且仅当 \(\forall l_j\le i < j,j > r_i\)。我们在二维平面上绘制 \(2n\) 条线段,分别为 \((i,i),(r_i,i)\) 和 \((i,l_i),(i,i)\),那么合法的充要条件就是这些线段互不在除 \((i,i)\) 以外的地方相交。如图(图是盗的):

现在假设固定了 \(l_i\)(即图中的缺口),设 \(p_i\) 为 \(i\) 后面第一个 \(l_j\le i\) 的 \(j\),那么 \(r_i\in[i,p_i)\),有 \(p_i-i\) 种取值。
我们考虑对图中的白色区域设状态计数,设 \(f_{i,j}\) 表示 \(\forall k\in[i,j],p_k\le j+1\) 且 \(l_{j+1} < l\) 时区间 \([l,r]\) 的答案,\(g_{l,r}\) 表示 \(\forall k\in[i,j],p_k\le j+1\) 且 \(l_{j+1} \ge l\) ,答案就是 \(f_{1,n}\)。
设 \(k\) 表示第一个满足 \(p_k=j+1\) 的 \(k\),即图中第一个紫色线段能延伸到末尾的位置,那么这个位置 \(k\) 可以把区间分成两个部分,这两部分是独立的,因为 \(r_k\) 有 \(j-k+1\) 种取值,于是有转移 \(f_{i,j}\larr g_{i,k-1}\times f_{k+1,j}\times (j+1-k)\)。同理有 \(g_{i,j}\larr g_{i,k-1}\times f_{k+1,j}\times (j+1-k)\times(k-i+1)\),其中 \(k-i+1\) 表示 \(l_{j+1}\in[i,k]\),有 \(k-i+1\) 种取值。
观察发现转移都只和区间长度有关,所以只需要记录 \(f_i,g_i\) 表示区间长度为 \(i\) 时的答案,初始化 \(f_0=g_0=1\),于是转移就是:
\(\mathcal{O}(n^2)\) 做即可。如果模数可以做多项式卷积的话,可以用分治 FFT 优化到 \(\mathcal{O}(n\log^2 n)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 5005;
int n,mod;
ll f[N],g[N],ans;
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();mod = rd();
f[0] = g[0] = 1;
for(int i = 1;i <= n;i++)for(int j = 1;j <= i;j++)
{
(f[i] += g[j-1]*f[i-j]%mod*(i-j+1)) %= mod;
(g[i] += g[j-1]*f[i-j]%mod*(i-j+1)*j) %= mod;
}
ans = f[n];for(int i = 1;i <= n;i++)(ans *= i) %= mod;
cout << ans << endl;
return 0;
}
[AGC067B] Modifications
有一个长度为 \(n\) 的序列和 \(m\) 个区间 \([l_i,r_i]\) 和一个数 \(C\),初始每个位置为 \(0\),每次操作可以选择一个区间和一个 \([1,C]\) 内的数,并将区间内都赋值为这个数,求最后能产生多少个本质不同的区间。答案对 \(998244353\) 取模。
\(n,C\le 100\)
考虑一个最终的序列 \(a\),怎么判断其是否合法?我们可以每次选一个区间出来,如果 \(a\) 在区间内所有数都相同,我们就可以把这个区间内所有数都赋值成 ?,然后一直做下去,看能否让整个序列都变成 ?。
然后套路地考虑区间 dp,设 \(f_{l,r}\) 表示只考虑完全被 \([l,r]\) 包含的区间,一共有多少个最终的序列 \(a\) 合法,如果这些区间的并集不为 \([l,r]\)。则 \(f_{l,r}=0\)。直接做不太好做,考虑容斥。即计算有多少个可能的最终的 ? 和数组成的序列,满足这个序列不全为 ?且不能被任意一个区间再操作,即对于任意一个区间,满足序列上这个区间中全为问号或存在两个数不同。
这个东西还是可以考虑 dp 去计算,我们发现一个位置只需要记录上一个与它不同的位置即可。设 \(g_{l,r,p}\) 表示区间 \([l,r]\) 中,钦定位置 \(r\) 为一个数,上一个与其不同的数的位置为 \(p\)。转移:
- 后面加了一个相同的数,枚举这个数的位置 \(k\):\(g_{l,k,p}\larr g_{l,r,p}\times f_{r+1,k-1}\)
- 后面加了一个不同的数,仍然是枚举位置:\(g_{i,k,r}\larr g_{l,rp}\times f_{r+1,k-1}\times(C-1)\)
然后转移的时候判断是否存在一个区间 \([l_i,r_i]\) 满足 \(p < l_i\le r\le r_i < k\),如果存在就不能转移,这部分可以提前预处理。时间复杂度 \(\mathcal{O}(n^4)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 105,mod = 998244353;
int mx[N][N],n,m,C;
ll b[N],f[N][N],g[N][N][N],s;
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();m = rd();C = rd();
for(int i = b[0] = 1;i <= n;i++)b[i] = b[i-1]*C%mod;
while(m--)
{
int l = rd(),r = rd();
for(int i = l;i <= r;i++)for(int j = r;j <= n;j++)
mx[i][j] = max(mx[i][j],l);
}
for(int i = 1;i < N;i++)f[i][i-1] = 1,g[i][i-1][i-1] = 1;
for(int len = 1;len <= n;len++)for(int l = 1,r;(r = l+len-1) <= n;l++)
{
for(int p = l-1;p < r;p++)
{
for(int k = p;k < r;k++)
if(k == p||p >= mx[k][r-1])(g[l][r][p] += g[l][k][p]*f[k+1][r-1]) %= mod;
for(int k = l-1;k <= p;k++)
if(k == p||k >= mx[p][r-1])(g[l][r][p] += g[l][p][k]*f[p+1][r-1]%mod*(C-1)) %= mod;
}
f[l][r] = b[len];
for(int k = l;k <= r;k++)for(int p = l-1;p < k;p++)
if(p >= mx[k][r])(f[l][r] += (mod-g[l][k][p])*f[k+1][r]) %= mod;
}
cout << f[1][n] << endl;
return 0;
}
[AGC062D] Walk Around Neighborhood
给定一个长度为 \(n\) 的序列 \(D_i\),\(D_i\) 为偶数。有一个人,初始在原点,每次他可以选择一个之前没选过的 \(i\),然后移动到任意一个距离自己曼哈顿距离为 \(D_i\) 的点上。经过 \(n\) 次移动后,要求他要回到原点,求整个过程中到达的所有点距离原点曼哈顿距离最大值的最小值。
\(n,D_i\le 2\times 10^5\)
将 \(D_i\) 从小到大排序,然后为了方便思考,把曼哈顿距离转化为切比雪夫距离,每次一个点就能走到一个正方形上的点。先考虑无解条件,如果 \(\sum\limits_{i=1}^{n-1}D_i < D_n\),那么一定无解,否则一定有解,且答案在 \([\frac {D_n} 2,D_n]\) 之间。
考虑证明,下限为 \(\frac{D_n}2\) 是显然的,因为要走 \(D_n\) 这一步。然后我们可以构造出一组答案为 \(D_n\) 的解出来,因为 \(\sum\limits_{i=1}^{n-1}D_i \ge D_n\),所以可以先用一些 \(D_i\) 走到距离原点边长为 \(D_n\) 的正方形上。接着除了最后一步 \(D_n\),因为 \(D_i < D_n\),所以可以一直在正方形边界上走,最后用一步 \(D_n\) 回去。于是就证明了答案一定在 \([\frac {D_n} 2,D_n]\) 内,现在我们考虑如何判断一个答案是否合法。
假设当前的答案是 \(r\),那么整个行走的过程都必须在距离原点半径为 \(r\) 的正方形内。我们尝试找到一种最优的策略,观察发现,我们的方案一定是先从原点走一些 \(D_i\) 到正方形边缘上,然后再在正方形边缘上随便走(因为 \(a_i\le \frac r 2\),所以一定可以一直停在正方形边上),最后再走一些 \(D_i\) 回到原点。
因为从原点走到正方形上和走回来是等价的,所以问题就是如何判断一个集合 \(D_i\) 能否从原点走到正方形边上。
设 \(s = \sum D_i[D_i < r]\),如果 \(s\ge r\),那么一定有解。现在考虑 \(s < r\) 且有 \(D_i \ge r\) 时的答案,可以发现对于一个 $ \ge r$ 的 \(D_i\) 最多只会用一个,因为每次走的时候要么直接无法走到半径为 \(r\) 的正方形内或者可以直接走到正方形边上。并且越小的 \(D_i\) 用不容易走出去,所以我们只会用最小的 $ \ge r$ 的 \(D_i\),记为 \(x\)。
而对于 \(<r\) 的 \(D_i\),因为 \(s < r\),而且在离原点越远的位置使用 \(x\) 越容易有解,所以一定会先走到离原点半径为 \(s\) 的正方形上,然后使用一次 \(x\),于是有解的条件就是 \(x-s\le r\)。
现在考虑枚举答案 \(r\),我们要把所有 \(D_i\) 分成两部分使得两部分都满足上述条件。因为有一个 \(\ge r\) 的 \(D_i\) 肯定比没有好,所以我们给两部分分别选出两个最小的 \(\ge r\) 的 \(D_i\),如果没有就不选,这样就可以计算出两个部分 \(s\) 的下界。于是问题就变成了能否将 \(<D_i\) 的部分分成两个集合,使得两个集合的值都分别 \(\ge\) 某个数。
根据上述条件我们发现,如果一个实数 \(x\) 可以作为答案且 \(x\ne \frac{a_n} 2\),那么 \(\lfloor x\rfloor\) 也一定可以作为答案。所以除了 \(\frac{a_n} 2\) 以外,其他答案一定是整数,于是我们可以直接枚举答案 \(r\),每次将所有 \(< r\) 的 \(D_i\) 加入背包,然后用一次 _Find_next 即可判断。时间复杂度 \(\mathcal{O}(\frac{n^2}\omega)\)。(默认值域与 \(n\) 同阶)
继续思考我们发现,如果当前 \(<r\) 的 \(D_i\) 的和已经很大了,那么一定可以将这些数分成两组使得这两组的和都 \(\ge r\)。具体来说,如果 \((\sum D_i[D_i < r])\ge 3r\),那么向一个集合中加入 \(D_i\) 直到集合的和第一次 \(\ge r\),剩下的数的和也一定 \(\ge r\)。
特判掉这种情况后,就只需要做 \(D_i\) 和为 \(\mathcal{O}(n)\) 的背包。于是 \(D_i\) 最多有 \(\mathcal{O}(\sqrt n)\) 种不同的值,可以使用二进制分组背包,复杂度为 \(\mathcal{O}(\frac{n\sqrt n}\omega)\)。
代码(n^2/w)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <bitset>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 2e5+5;
int a[N],n;
bitset<N> f;
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();
for(int i = 1;i <= n;i++)a[i] = rd();
sort(a+1,a+n+1);f[0] = 1;ll s = 0;
for(int i = a[n]/2,j = 1;i <= a[n];i++)
{
while(a[j] < i)f |= f<<a[j],s += a[j++];
int x = a[j]-i,y = j==n?i:a[j+1]-i;
if(s-(int)f._Find_next(x-1) >= y)return printf("%d\n",i),0;
}
puts("-1");
return 0;
}
[AGC045D] Lamps and Buttons
有 \(n\) 盏灯和 \(n\) 个开关和一个隐藏的排列 \(p\),初始前 \(A\) 盏灯是亮的,其余是暗的,第 \(i\) 个开关控制第 \(p_i\) 盏灯。每次你可以选择一个亮着的灯 \(i\),并按下第 \(i\) 个开关,并且随时都可以看到 \(n\) 盏灯是否是亮着的,最后如果 \(n\) 盏灯都亮了就获胜。求在采取最优策略下,最多有多少个排列 \(p\) 能获胜。对 \(10^9+7\) 取模。
\(A\le 5000,n\le 10^7\)
首先考虑最优策略是什么。因为每盏灯都是等价的,所以我们不妨按下第一盏灯,然后如果第一盏灯指向自己,那就直接失败。否则一定可以将第一盏灯所在置换环上的灯全部点亮。然后点下一盏亮着且没在之前的环中的灯,一直重复下去直到所有灯都亮起。
接下来考虑哪些情况可能会导致失败,第一种是在所有灯都还没全亮时点到了自环,第二种是把能点亮的环都点亮后仍有未被点亮的灯。
那么考虑一个合法的排列 \(p\) 应该满足哪些性质,设 \(p\) 中第一个自环的位置是 \(x\),那么应该在碰到 \(x\) 之前就已经把所有灯都点亮了,即所有 \([A+1,n]\) 中的灯所在置换环中都存在至少一个位置是 \(<x\) 的。接下来要求答案,首先枚举第一个自环的位置 \(x\)。
然后有两个限制,第一个是关于置换环的,第二个是 \(<x\) 的灯中没有自环。第二个限制比较不好处理,考虑容斥,钦定前 \(x-1\) 盏灯中有 \(i\) 盏灯为自环,于是把排列分成三部分,第一部分为 \([1,x-1]\) 的灯,第二部分为 \([x+1,A]\),第三部分为 \([A+1,n]\)。问题就是计数有多少个排列满足所有第三部分中的数的置换环中至少有一个数在第一部分。
把问题简化为有 \(a,b,c\) 三个部分,我们考虑一个一个将数插入到前面的数形成的置换环中。先加入第一部分的数,有 \(a!\) 种,然后加入第三部分的数,因为每次加入必须加入到之前的某一个置换环种,而不能单独成环,所以方案数为 \(a(a+1)(a+2)\ldots(a+c-1)\)。最后插入第二部分,这部分没有限制,方案数为 \((a+c+1)(a+c+2)\ldots(a+b+c)\)。于是总方案数为 \(\frac{(a+b+c)!a}{a+c}\)。然后就可以 \(\mathcal{O}(A^2+n)\) 做了。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 1e7+5,mod = 1e9+7;
int n,m;
ll fac[N],inv[N],invfac[N],ans;
inline ll C(int n,int m){return fac[n]*invfac[m]%mod*invfac[n-m]%mod;}
inline ll calc(int x,int y,int z){return fac[x+y+z]*x%mod*inv[x+z]%mod;}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();m = rd();fac[0] = inv[1] = invfac[0] = 1;
for(int i = 2;i <= n;i++)inv[i] = (mod-mod/i)*inv[mod%i]%mod;
for(int i = 1;i <= n;i++)fac[i] = fac[i-1]*i%mod,invfac[i] = invfac[i-1]*inv[i]%mod;
for(int i = 1;i <= m+1;i++)for(int j = 0;j < i;j++)
(ans += (j&1?-1:1)*C(i-1,j)*calc(i-1-j,max(0,m-i),n-m)) %= mod;
cout << (ans+mod)%mod << endl;
return 0;
}
[AGC036E] ABC String
给定一个只包含字符 ABC 的字符串 \(S\),你需要求出 \(S\) 最长的子序列,满足子序列中相邻的两个位置字符不同,且 ABC 的数量相等。
\(|S|\le 10^6\)
我们考虑一个一个删除 \(S\) 中的字符来得到最长的子序列,首先先将 \(S\) 中相同的字母缩成一段。设三个字母的出现次数分别为 \(C_{A},C_{B},C_{C}\),不妨设 \(C_{A}\le C_{B}\le C_{C}\),那么答案的上限为 \(C_{A}\),于是我们要删除字符使 \(C_{A}=C_{B}=C_{C}\),且删除的字符的数量尽量少。
我们先考虑 \(C_{A}\le C_{B}=C_{C}\) 的情况,这个时候字符串肯定长成 \(CB\ldots BCABC\ldots CBACB\ldots BC\ldots CB\) 这样的形式,即两个 \(A\) 之间有一串 \(BC\ldots BC\),这个时候我们每次删相邻两个 BC 或 CB,那么一定可以删到 \(C_{A}=C_{B}=C_{C}\),于是此时的答案就是 \(C_{A}\)。
如果是 \(C_{A}\le C_{B}\le C_{C}\) 的情况,我们目标就是在删除尽量少的 \(A\) 的情况下删除 C 直到 \(C_{A}\le C_{B}=C_{C}\)。于是可以先考虑能否删除每个 C,然后如果仍然没满足条件,就删 AC 或 CA,直到 \(C_{A}\le C_{B}=C_{C}\) 即可,这样一定是最优的。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
const int N = 1e6+5;
int c[128],pre[N],nex[N],n;
char s[N],id[3] = {'A','B','C'};
inline bool pd(int x,int y){return !pre[x]||nex[y] > n||s[pre[x]] != s[nex[y]];}
inline void erase(int x){nex[pre[x]] = nex[x];pre[nex[x]] = pre[x];}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
scanf("%s",s+1);n = strlen(s+1);
for(int i = 0;i <= n+1;i++)pre[i] = i-1,nex[i] = i+1;
for(int i = 1,lst = 0;i <= n;i++)
if(s[i] != s[lst])c[s[i]]++,lst = i;
else erase(i);
sort(id,id+3,[](char x,char y){return c[x] < c[y];});
for(int i : {0,1,2})c[i] = c[id[i]];
for(int i = nex[0];i <= n&&c[2] > c[1];i = nex[i])
if(s[i] == id[2]&&pd(i,i))erase(i),c[2]--;
for(int i = nex[0];i <= n&&c[2] > c[1];i = nex[i])
if(s[i]+s[nex[i]] == id[0]+id[2]&&pd(i,nex[i]))erase(i),erase(i = nex[i]),c[2]--,c[0]--;
for(int i = nex[0];i <= n&&c[1] > c[0];i = nex[i])
if(s[i]+s[nex[i]] == id[1]+id[2]&&pd(i,nex[i]))erase(i),erase(i = nex[i]),c[2]--,c[1]--;
for(int i = nex[0];i <= n;i = nex[i])printf("%c",s[i]);
return 0;
}
[AGC039F] Min Product Sum
有一个大小为 \(n\times m\),每个数在 \([1,k]\) 内的矩阵 A,定义 \(f(x,y)\) 表示第 \(x\) 行和第 \(y\) 列共 \(n+m-1\) 个数中的最小值。定义矩阵 A 的权值为 \(\prod\limits_{x=1}^n\prod\limits_{y=1}^m f(x,y)\)。你需要求出所有 \(k^{nm}\) 个矩阵的权值和。对某个质数取模。
\(n,m,k\le 100\)
如果一个大小为 \(n\times m\),每个数在 \([1,k]\) 内的矩阵 B 满足 \(\forall x,y,B_{x,y}\le f(x,y)\),那么答案就是计数有多少个 \((A,B)\) 这样的矩阵对。
考虑 \(\forall x,y,B_{x,y}\le f(x,y)\) 这个条件相当于什么,即 \(A\) 每一行的所有数都大于等于 \(B\) 对应这一行中的数,即 \(A\) 这一行的最小值大于等于 \(B\) 这一行的最大值,列同理。接下来考虑怎么计数,如果你注意力惊人,那么就有一个很牛的 dp:
我们从值域上考虑,依次枚举 \(1\sim k\),然后将 \(A\) 其中一些列的 \(\min\) 和 \(B\) 其中一些行的 \(\max\) 设为 \(k\),并确定一些位置的取值。设 \(f_{t,i,j}\) 表示考虑了值域 \(1\sim t\),\(A\) 确定了 \(i\) 列的 \(\min\),\(B\) 确定了 \(j\) 行的 \(\max\) 的方案数。
假设当前枚举的值为 \(x\),我们先考虑将 \(B\) 的某一行的 \(\max\) 赋为 \(k\),然后考虑哪些位置的值的范围能被确定。首先对于矩阵 A,要求 A 中对应这一行的 \(\min\ge k\),即所有数都 \(\ge k\)。对于 A 中还未确定 \(\min\) 的列,因为这些数的 \(\min\) 还未确定,所以一定都 \(\ge k\),先暂时不考虑。对于那些已经确定了 \(\min\) 的列,我们一定可以确定这些数的范围在 \([x,k]\),于是方案数为 \((k-x+1)^i\)。
对于 \(B\),如果一列之前已经确定了最小值,那么这个位置一定 \(<k\),所以不会造成影响。于是就要求剩下 \(m-i\) 个位置的 \(\max=k\),方案数为 \(k^{m-i}-(k-1)^{m-i}\)。
然后考虑确定了 \(A\) 的一行 \(\min=k\),先考虑 \(A\),仍然用上面的分析方法,得出要求 \(A\) 中 \(j\) 个位置 \(\min=k\),于是方案数为 \((k-x+1)^j-(k-x)^j\)。B 中则要求 \(n-j\) 个位置要 \(\le n-j\),方案数为 \(x^{n-j}\)。
这个时候 dp 就做完了,我们每次在 A 中一个位置两次被覆盖的时候计算这个位置的取值方案,在 B 中一个位置第一次被覆盖时计算。转移的时候把一行或一列变成枚举 \(p\) 行或 \(p\) 列,总复杂度为 \(\mathcal{O}(n^4)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 105;
int n,m,k,mod;
ll C[N][N],f[N][N][N],g[N][N][N];
ll qp(ll x,ll y)
{
ll ans = 1;
for(;y;y >>= 1,x = x*x%mod)
if(y&1)ans = ans*x%mod;
return ans;
}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();m = rd();k = rd();mod = rd();g[0][0][0] = 1;
for(int i = 0;i < N;i++)for(int j = C[i][0] = 1;j <= i;j++)
C[i][j] = (C[i-1][j-1]+C[i-1][j])%mod;
for(int x = 1;x <= k;x++)
{
for(int i = 0;i <= m;i++)for(int j = 0;j <= n;j++)
{
ll sum = 1,mul = (qp(x,m-i)-qp(x-1,m-i)+mod)*qp(k-x+1,i)%mod;
for(int p = j;p <= n;p++,sum = sum*mul%mod)
(f[x][i][p] += C[n-j][p-j]*g[x-1][i][j]%mod*sum) %= mod;
}
for(int i = 0;i <= m;i++)for(int j = 0;j <= n;j++)
{
ll sum = 1,mul = (qp(k-x+1,j)-qp(k-x,j)+mod)*qp(x,n-j)%mod;
for(int p = i;p <= m;p++,sum = sum*mul%mod)
(g[x][p][j] += C[m-i][p-i]*f[x][i][j]%mod*sum) %= mod;
}
}
cout << g[k][m][n] << endl;
return 0;
}
[AGC008F] Black Radius
有一棵 \(n\) 个点的树和一个集合,你可以选择一个集合中的点和一个 \(r\),然后求出所有距离这个点不超过 \(r\) 的点构成的集合,求能构成多少种不同的集合。
\(n\le 2\times 10^5\)
首先特判掉集合是整个树的情况。设 \((x,r)\) 表示距离 \(x\) 不超过 \(r\) 的邻域构成的集合。我们发现,如果 \((x_1,r_1) = (x_2,r_2)\),那么一定是 \((x_1,x_2)\) 这条路径上有至多一棵子树有一半是集合内的,有一半不是集合内的。
此时如果 \(r_1 < r_2\),我们可以让 \(x_2\) 往 \(x_1\) 挪一条边,然后 r2--,这样子邻域还是相同的。如果 \(r1=r2\),那么路径上一定有个中点,我们让 \(x1,x2\) 都向中点挪一条边,再 r1--,r2--,则邻域依然是相同的。那么对于同一个邻域的所有表示,\(r\) 最小的表示一定是唯一的,我们可以对这些 \((x,r)\) 作为代表计数。也就是说,一个 \((x,r)\) 能被计数当且仅当不存在一个 \((y,r'),r' < r\),使得 \((x,r)=(y,r')\)。
又根据上面的证明,我们可以得出一个 \((x,r)\) 合法,当且仅当不存在一个与 \(x\) 相连的 \(y\) 满足 \((x,r) = (y,r-1)\)。所以对于一个点 \(x\),合法的 \(r\) 一定是一段前缀,我们考虑求出这个分界点是什么。
首先邻域不能是整棵树,我们设 \(mx_u\) 表示距离最远的点的距离,则 \(r\le mx_u\)。然后我们考虑求出最小的 \(r\),使得存在 \((y,r-1)=(x,r)\)。这个时候空一半的子树一定是 \(mx_u\) 所在的子树,我们取其余子树中的点的距离最大值,设为 \(se_u\)。那么我们可以取 \(u\) 的 \(mx_u\) 所在子树的儿子 \(v\),有 \((u,se_u+2) = (v,se_u+1)\),这个限制是最严的,所以得出 \(r\le \min(se_u+1,mx_u-1)\)。
这个时候如果所有点都在集合内就做完了,我们可以对每个点换根 dp 求出 \(mx_u,se_u\),然后把上界加起来即可。但如果一个点不在集合内,它的一个邻域 \((x,r)\) 合法,当且仅当存在一个在集合内的点,且这个点的某个邻域与 \((x,r)\) 相同。这相当于是 \(r\) 的一个下界,于是一个点 \(u\) 符合条件的 \(r\) 是一段区间。
怎么求出这个下界呢?如果一个 \(x\) 的某个邻域与一个在集合内的点 \(y\) 的某个邻域相等,那么这个点必须包含 \(y\) 所在 \(x\) 的儿子的子树内的所有点,于是找出这个子树内距离最大的点。所以一个点 \(x\) 的答案就是以 \(x\) 为根,枚举 \(x\) 的每个儿子,如果儿子内存在一个集合内的点,那么答案就和这个子树的最大深度取 \(\min\)。这一部分也可以在换根 dp 时求出。
时间复杂度 \(\mathcal{O}(n)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 2e5+5;
int hd[N],cnt,siz[N],mx[N],se[N],d[N],n;
bool vis[N];ll ans;
struct node{int to,nex;}e[N << 1];
inline void add(int u,int v)
{e[++cnt] = {v,hd[u]};hd[u] = cnt;}
void dfs1(int u,int fa)
{
if(vis[u])siz[u] = 1,d[u] = 0;
else d[u] = N;
for(int i = hd[u],v;i;i = e[i].nex)
{
if((v = e[i].to) == fa)continue;
dfs1(v,u);siz[u] += siz[v];int x = mx[v]+1;
if(x >= mx[u])se[u] = mx[u],mx[u] = x;
else se[u] = max(se[u],x);
if(siz[v])d[u] = min(d[u],x);
}
}
void dfs2(int u,int fa)
{
ans += max(0,min(mx[u]-1,se[u]+1)-d[u]+1);
for(int i = hd[u],v;i;i = e[i].nex)
{
if((v = e[i].to) == fa)continue;
int x = mx[u] == mx[v]+1?se[u]+1:mx[u]+1;
if(x >= mx[v])se[v] = mx[v],mx[v] = x;
else se[v] = max(se[v],x);
if(siz[1] > siz[v])d[v] = min(d[v],x);
dfs2(v,u);
}
}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
inline char gc()
{char c;while((c = getchar()) <= ' ');return c;}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();
for(int i = 1;i < n;i++)
{int u = rd(),v = rd();add(u,v);add(v,u);}
for(int i = 1;i <= n;i++)vis[i] = gc()-'0';
dfs1(1,0);dfs2(1,0);
cout << ans+1 << endl;
return 0;
}
[ARC122F] Domination
给定二维平面上的 \(n\) 个红点和 \(m\) 个蓝点,要求移动蓝点,使每个红点的右上方都至少有 \(k\) 个蓝点。将位于 \((x_1,y_1)\) 的蓝点,移动到 \((x_2,y_2)\) 的代价为 \(|x_1-x_2|+|y_1-y_2|\),求最小代价。
\(n,m\le 10^5,k\le 10\)
首先一个红点如果在另一个点的左下方,那么这个点就没有用,可以去除这些点。此时剩下的红点满足 \(x\) 递增,\(y\) 递减。
我们将一个蓝点 \((bx_j,by_j)\) 移动到某个位置,那么这个蓝点能覆盖的红点一定是一段区间,区间左端点为最小的 \(i\) 满足 \(ry_i\le by_j\),右端点为最大的 \(i\) 满足 \(rx_i\le bx_j\),我们发现 \(x,y\) 轴时独立的。
先考虑 \(k=1\) 怎么做。我们用最短路的思想,一个蓝点覆盖如果一个区间 \([l,r]\),那么就相当于第 \(l\) 个红点向蓝点连边,然后蓝边向第 \(r+1\) 个红点连边,两条边权和为移动的代价。然后求第一个红点到第 \(n+1\) 个红点的最短路长度。
于是我们就得出了建边方式:第 \(i\) 个红点向第 \(j\) 个蓝点连边 \(\max(0,ry_i-by_j)\),第 \(j\) 个蓝点向第 \(i+1\) 个红点连边 \(\max(0,rx_i-bx_j)\),然后跑最短路即可。因为边有 \(\mathcal{O}(nm)\) 条,于是我们可以用前后缀优化建图将边数优化到 \(\mathcal{O}(n+m)\)。
现在要求每个红点右上方必须有 \(k\) 个蓝点,于是可以考虑费用流,将每个蓝点拆成入点和出点,这两个点之间连流量 \(1\),费用 \(0\) 的。其余最短路的边流量无限,费用就是边权,然后从起始点流 \(k\) 的流量的最小费用就是答案。剩下的就是费用流板子了,我们发现边权非负,所以可以跑 dijkstra 费用流,时间复杂度为 \(\mathcal{O}(k(n+m)\log(n+m))\)。
dijkstra 费用流:每次跑费用流时,因为要求最短路,而边权有可能非负,所以可以向 Johnson 求最短路一样给每个点赋一个势能 \(h_u\),然后 \((u,v)\) 的边的边权就是 \(h_u+w_{u,v}-h_v\)。因为每次跑最短路都要求边权非负,所以每次跑完最短路都让 \(h_u += dis_u\) 即可。可以证明每次的边权都非负。其余东西和费用流一样。(具体可以看代码)
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <utility>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 7e5+5,M = 2e6+5;
int n,m,k,s,t,mxf;
int hd[N],rad[N],cnt = 1;
ll dis[N],h[N],mic;bool vis[N];
struct edge{int to,nex,f,w;}e[M << 1];
struct node{int x,y;}a[N],b[N];
inline void add(int u,int v,int f,int w)
{e[++cnt] = {v,hd[u],f,w};hd[u] = cnt;}
inline void adde(int u,int v,int f,int w){add(u,v,f,w);add(v,u,0,-w);}
priority_queue<pair<ll,int> > q;
bool dijkstra()
{
for(int i = 1;i < N;i++)h[i] += dis[i],dis[i] = 1e18;
q.push({dis[s] = 0,s});
while(!q.empty())
{
int u = q.top().second;q.pop();
if(vis[u])continue;
vis[u] = 1;rad[u] = hd[u];
for(int i = hd[u];i;i = e[i].nex)if(e[i].f)
{
int v = e[i].to;ll w = dis[u]+h[u]-h[v]+e[i].w;
if(w < dis[v])dis[v] = w,q.push({-dis[v],v});
}
}
memset(vis,0,sizeof vis);
return dis[t] != 1e18;
}
int dfs(int u,int flow)
{
if(u == t)return flow;
int res = flow;vis[u] = 1;
for(int &i = rad[u],v;i&&res;i = e[i].nex)
{
if(vis[v = e[i].to]||!e[i].f||dis[v] != dis[u]+h[u]-h[v]+e[i].w)continue;
int now = dfs(v,min(res,e[i].f));
e[i].f -= now;e[i^1].f += now;res -= now;
mic += e[i].w*now;
}
return vis[u] = 0,flow-res;
}
int dinic()
{
int ans = 0;
while(dijkstra())ans += dfs(s,k);
return ans;
}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();m = rd();k = rd();int nn = 0;
for(int i = 1;i <= n;i++)a[i] = {rd(),rd()};
for(int i = 1;i <= m;i++)b[i] = {rd(),rd()};
sort(a+1,a+n+1,[](node x,node y){return x.y != y.y?x.y > y.y:x.x > y.x;});
for(int i = 1,sh = -1;i <= n;i++)
if(a[i].x > sh)sh = a[i].x,a[++nn] = a[i];
t = 5*nn+1;s = 5*nn+2*m+2;adde(s,4*nn+1,k,0);
for(int i = 1;i <= nn;i++)
{
int x = 4*nn+i;
adde(x,i,k,0);adde(x,nn+i,k,0);adde(2*nn+i,x+1,k,0);adde(3*nn+i,x+1,k,0);
if(i < nn)adde(i,i+1,k,a[i].y-a[i+1].y),adde(2*nn+i,2*nn+i+1,k,a[i+1].x-a[i].x);
if(i > 1)adde(nn+i,nn+i-1,k,0),adde(3*nn+i,3*nn+i-1,k,0);
}
for(int i = 1;i <= m;i++)
{
int x = 5*nn+1+i*2-1,y = x+1;
adde(x,y,1,0);
int p = lower_bound(a+1,a+nn+1,b[i],[](node x,node y){return x.y > y.y;})-a-1;
int q = lower_bound(a+1,a+nn+1,b[i],[](node x,node y){return x.x < y.x;})-a;
if(p >= 1)adde(p,x,k,a[p].y-b[i].y);
if(p < nn)adde(nn+p+1,x,k,0);
if(q <= nn)adde(y,2*nn+q,k,a[q].x-b[i].x);
if(q > 1)adde(y,3*nn+q-1,k,0);
}
mxf = dinic();cout << mic << endl;
return 0;
}
[AGC061F] Perfect Strings
给定正整数 \(n,m\),一个 01 串是好的,当且仅当串中 0 的个数是 \(n\) 的倍数,1 的个数是 \(m\) 的倍数。一个 01 串是完美的,当且仅当这个串是好的,且任何一个非空子串都不是好的。求有多少个 01 串是完美的。
\(n,m\le 40\)
设 \(x_i\) 表示前 \(i\) 个数中 \(0\) 的个数 \(\bmod n\) 的结果,\(y_i\) 表示前 \(i\) 个数中 \(1\) 的个数 \(\bmod m\) 的结果,那么串合法当且仅当 \(x_n=0,y_n=0\) 且不存在两个 \(0\le i<j< n\) 使得 \((x_i,y_i)=(x_j,y_j)\)。把 \((x_i,y_i)\) 看成坐标,就是在一个左下角为 \((0,0)\),右上角为 \((n-1,m-1)\) 的网格上。问题就是求有多少条路径,要求从原点出发,每次向上或向右走,走过边界就从另一边回来,最后回到原点,且路径除原点外不能相交。
路径不相交,可以联想到 LGV 引理。我们发现一条路径一定有若干个出口和入口,假设我们确定了这些入口,那么对面的出口也可以确定,要使路径不相交,合法的方案一定只能是从左上到右下依次匹配一个入口和出口。
我们将入口按最左一列从上到下,最下一行从左到右依次标号,现在一共有 \(n+m\) 个可能的入口,假设我们钦定了哪些位置是入口,怎么判断这是否是一种合法的选择、应该怎么求方案数?
首先要从起点出发,所以 \(n,n+1\) 中必须有且只有一个入口,并且因为这是一条路径,所以设最左一列有 \(x\) 个入口,最下一行有 \(y\) 个入口,应该满足 \(\gcd(x,y)=1\),要不然这就不是一条路径了。如果以上两个条件都满足,那么求方案数就是 LGV 引理板子了。注意最后入口对应出口并不是一一对应,而是类似 \(123456\) 对应 \(456123\) 这样,所以会有 \(x\times y\) 个逆序对,所以求出答案后要乘上 \((-1)^{x\times y}\)。
显然我们不可能暴力枚举 \(2^{n+m}\) 中情况。先不考虑 \(n,n+1\) 中必须有入口的限制,我们考虑用生成函数的思想,将矩阵中 \(1\sim n\) 的入口到每个出口的方案数乘上一个元 \(x\),\(n+1\sim m\) 的入口到每个出口的方案数乘上 \(y\)。然后因为可能不选一个入口,所以将所有一个入口到对面的出口的方案数加上 \(1\),相当于不选这个入口,即将所有 \(f_{i,i}\) 加一。
此时求行列式会得出一个关于 \(x,y\) 的 \(n+m\) 次多项式,那么左边有 \(a\) 个出口,下面有 \(b\) 个出口的方案数就是 \([x^ay^b]F(x,y)\)。显然求这个多项式不能暴力求行列式,于是可以考虑二维拉差,将所有 \(0\le x\le n,0\le y\le m\) 的 \((x,y)\) 带进去即可。
最后再加上必须有入口的限制,就是先不让 \(f_{n,n}\) 加一求一次行列式,然后再不让 \(f_{n+1,n+1}\) 加一求一次行列式,两次的多项式加起来即可。
二维拉差:如果有一个 \(x\) 最高为 \(n\) 次,\(y\) 最高为 \(m\) 次的多项式 \(F(x,y)\),现在已知对于所有 \(0\le i\le n,0\le j\le m\) 的 \((i,j)\),有 \(F(x_i,y_j)=f_{i,j}\),那么可以确定出原多项式:
\[F(x,y) = \sum_{i=0}^n\sum_{j=0}^m f_{i,j}(\prod_{p=0,p\ne i}^n \frac{x-x_p}{x_i-x_p})(\prod_{q=0,q\ne j}^m\frac{y-y_q}{y_j-y_q}) \]
时间复杂度为 \(\mathcal{O}(nm(n+m)^3)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 85,mod = 998244353;
int n,m;
ll F[N][N],a[N][N],b[N][N],C[N][N],f[N][N],g[N][N],h[N],ans;
inline ll inv(ll x ){return x==1?1:(mod-mod/x)*inv(mod%x)%mod;}
void init(ll *f,int x,int n)
{
f[0] = 1;
for(int i = 0;i <= n;i++)if(i != x)
{
memcpy(h,f,sizeof h);
for(int j = 0;j <= n;j++)
f[j] = ((j?h[j-1]:0)+h[j]*(mod-i))%mod;
}
}
ll det(int n)
{
ll ans = 1;
for(int i = 1;i <= n;i++)for(int j = 1;j <= n;j++)a[i][j] %= mod;
for(int i = 1;i <= n;i++)
{
int k = i;
for(int j = i;j <= n;j++)
if(a[j][i]){k = j;break;}
swap(a[i],a[k]);
if(i != k)ans = -ans;
if(!a[i][i])return 0;
(ans *= a[i][i]) %= mod;
for(k = 1;k <= n;k++)if(i != k)
{
ll s = a[k][i]*inv((a[i][i]+mod)%mod)%mod;
for(int j = i;j <= n;j++)
(a[k][j] -= a[i][j]*s) %= mod;
}
}
return (ans+mod)%mod;
}
inline ll get(int x,int y){return x < 0||y < 0?0:C[x+y][x];}
inline ll calc(ll x,ll y)
{
for(int i = 1;i <= n+m;i++)
{
int x1 = max(0,n-i),y1 = max(0,i-1-n);
for(int j = 1;j <= n+m;j++)
{
int x2 = j<=n?n-j:n-1,y2 = j>n?j-1-n:m-1;
b[i][j] = get(x2-x1,y2-y1)*(i<=n?x:y);
}
b[i][i]++;
}
memcpy(a,b,sizeof a);a[n][n]--;
ll ans = det(n+m);
memcpy(a,b,sizeof a);a[n+1][n+1]--;
return (ans+det(n+m))%mod;
}
int gcd(int x,int y){return y?gcd(y,x%y):x;}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();m = rd();
for(int i = 0;i < N;i++)for(int j = C[i][0] = 1;j <= i;j++)
C[i][j] = (C[i-1][j-1]+C[i-1][j])%mod;
for(int i = 0;i <= n;i++)init(f[i],i,n);
for(int j = 0;j <= m;j++)init(g[j],j,m);
for(int i = 0;i <= n;i++)for(int j = 0;j <= m;j++)
{
ll x = calc(i,j),s = 1;
for(int p = 0;p <= n;p++)if(p != i)(s *= i-p) %= mod;
for(int q = 0;q <= m;q++)if(q != j)(s *= j-q) %= mod;
s = inv((s+mod)%mod);
for(int p = 0;p <= n;p++)for(int q = 0;q <= m;q++)
(F[p][q] += x*s%mod*f[i][p]%mod*g[j][q]) %= mod;
}
for(int i = 0;i <= n;i++)for(int j = 0;j <= m;j++)
if(gcd(i,j) == 1)(ans += (i*j&1?mod-1:1)*F[i][j]) %= mod;
cout << ans << endl;
return 0;
}
[AGC057E] RowCol/ColRow Sort
给定一个 \(n\times m\),值域 \([0,9]\) 的矩阵 B,求有多少个 \(n\times m\) 的矩阵 A,满足:
- 分别对 A 的 每一列 中元素从小到大排序,再分别对 A 的 每一行 中元素从小到大排序能够得到 B。
- 分别对 A 的 每一行 中元素从小到大排序,再分别对 A 的 每一列 中元素从小到大排序能够得到 B。
\(n,m\le 1500\)
首先思考只有 \(0,1\) 怎么做,设 \(a_i\) 表示第 \(i\) 行 \(0\) 的个数,\(b_j\) 表示第 \(j\) 列 \(0\) 的个数。那么先对行排序,就是将每行的 \(a_i\) 个 \(0\) 放到左边,再对列排序就是将 \(a_i\) 从大到小排序。先对列,再对行排序就是将 \(b_j\) 从大到小排序。于是一个矩阵 A 合法,当且仅当它的 \(a_i\) 构成的可重集与 B 的 \(a_i\) 的可重集相等,A 的 \(b_j\) 构成的可重集与 B 的 \(b_j\) 相等。
进一步可以发现,如果知道了 A 的所有 \(a_i,b_j\),那么我们一定可以确定 A 是什么。因为排序后是个杨表结构,于是我们一定可以通过,依次从大到小枚举 \(a_i\),此时一定恰好有 \(a_i\) 个 \(b_j > 0\),将这些位置填上 \(1\),然后将这些 \(b_j\) 减一,一直做下去来唯一确定 A。所以一个矩阵 A 合法,当且仅当存在两个排列 \(p_i,q_j\),使得 \(\forall i,j,A_{i,j}=B_{p_i,q_j}\)。那么答案就是两个可重集的排列数相乘,即:
然后考虑值域为 \([0,9]\) 怎么办,还是先看怎么判合法。我们枚举 \(k\in[0,9]\),每次将 A 和 B 中 \(<k\) 的数设为 \(0\),\(\ge k\) 的数设为 \(1\),然后看这两个 01 矩阵是否合法。如果对于每个 \(k\) 都合法,那么矩阵 B 就合法。于是条件就是存在一组排列 \((p_0,q_0,p_1,q_1\ldots,p_9,q_q)\),满足 \(\forall 0\le k\le 9,1\le i\le n,1\le j\le m,[A_{i,j}\le k] = [B_{p_{k,i},q_{k,j}}\le k]\)。
上述条件的必要性显然,充分性考虑我们枚举 \(k\),每次将 A 的 01 矩阵相较于上一次多出来的 \(0\) 的部分的值设为 \(k\),于是这一组排列就一定能对应一个合法 \(A\)。因为存在一组排列这个条件不好做,我们还是考虑去计数有多少组排列满足条件,最后对每个 \(k\),除以重复的方案数(和上面的可重集计数一样)。
现在考虑计数有多少组排列,依次枚举 \(k\),现在问题是知道了上两个排列 \(p_{k-1},q_{k-1}\),求现在有多少个排列 \(p_k,q_k\)。那么思考 \(p_k,q_k\) 应该满足哪些条件,因为 A 中在 \(k-1\) 是 \(0\) 的位置在 \(k\) 时也必须是 \(0\),也就是说 \(A_{i,j} < k\Rightarrow A_{i,j}\le k\),在 B 中就是 \(B_{p_{k-1,i},q_{k-1,j}} < k\Rightarrow B_{p_{k,i},q_{k,j}}\le k\)。于是问题就是给定两个排列 \(p',q'\),求有多少个排列组 \((p,q)\),满足 \(\forall B_{p'_i,q'_j} < k,B_{p_i,q_j}\le k\)。显然 \(p',q'\) 具体是什么不重要,只需要知道和 \(p'^{-1}\times p,q'^{-1}\times q\) ,即两组排列的相对关系即可。所以我们可以直接钦定 \(p'_i=i,q'_j=j\),计数 \((p,q)\) 满足 \(\forall B_{i,j} < k,B_{p_i,q_j}\le k\)。
因为 B 中 \(\le k\) 的部分是一个杨表结构,所以一个位置小于一个数的条件可以简化。设 \(a_i\) 表示 B 的第 \(i\) 行中最后一个 \(<k\) 的位置,\(b_j\) 表示 B 的第 \(j\) 列中最后一个 \(\le k\) 的位置。于是条件就是 \(\forall j\le a_i,p_i\le b_{q_j}\)。因为 \(b\) 是递减的,那么对于一个 \(i\),条件最严的肯定是 \(q_j\) 最大的。所以改写条件为 \(p_i\le b_{\max\limits_{j=1}^{a_i} q_j}\)。现在考虑计数 \(c_i=\max\limits_{j=1}^{a_i} q_j\),如果我们求出了 \(c_i\),那么可以分别算出有多少个 \(p,q\)。
对于 \(p\),有 \(p_i\le b_{c_i}\) 的限制,因为 \(a_i\) 递减,所以 \(\max\limits_{j=1}^{a_i} q_j\) 递减,又因为 \(b\) 递减,所以 \(b_{c_i}\) 递增。所以 \(p\) 的个数为 \(\prod\limits_{i=1}^n b_{c_i}-i+1\)。
对于 \(q\),我们枚举每个 \(i\),如果 \(c_i=c_{i-1}\),那么说明在 \((a_i,a_{i-1}]\) 中没有出现最大值,那么前 \(a_i\) 个数一定有一个是最大值 \(c_i\),于是 \((a_i,a_{i-1}]\) 中第一个数有 \(c_i-1-(a_i-1)=c_i-a_i\) 种选法,第二个数有 \(c_i-a_i-1\) 种选法,一直下去,可以得出贡献为 \(\frac{(c-a_i)!}{(c-(a_{i-1}-a_i))!}\)。
如果 \(c_i < c_{i-1}\),那么说明最大值在 \((a_i,a_{i-1}]\) 中,每个位置是最大值是等价的,类似的我们可以算出贡献为 \((a_{i-1}-a_i)\times \frac{(c-a_i-1)!}{(c-(a_{i-1}-a_i))!}\)。
于是我们可以 dp,设 \(f_{i,j}\) 表示前 \(i\) 个数,\(c_i=j\) 的方案数。转移时发现贡献与 \(j\) 无关,所以可以直接前缀和优化,做到 \(\mathcal{O}(n^2)\) 的复杂度。我们对每个 \(k\) 都这么做一遍,把答案乘起来,最后除以系数即可。总复杂度 \(\mathcal{O}(10n^2)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 1505,mod = 998244353;
int B[N][N],a[15][N],b[15][N],c[N],n,m;
ll f[N][N],s[N],fac[N],inv[N],ans = 1;
ll get(int *a,int n,int m)
{
memset(c,0,sizeof c);ll ans = 1;
for(int i = 1;i <= n;i++)c[a[i]]++;
for(int i = 0;i <= m;i++)(ans *= inv[c[i]]) %= mod;
return ans;
}
inline ll A(int n,int m){return m<0||m>n?0:fac[n]*inv[n-m]%mod;}
ll solve(int *a,int *b)
{
memset(f,0,sizeof f);a[0] = m;b[0] = n;
f[0][m] = 1;
for(int i = 1;i <= n+1;i++)
{
int len = a[i-1]-a[i];
for(int j = m;j;j--)s[j] = (s[j+1]+A(j-a[i]-1,len-1)*len%mod*f[i-1][j])%mod;
for(int j = 0;j <= m;j++)
f[i][j] = (f[i-1][j]*A(j-a[i],len)+s[j+1])%mod*(i==n+1?1:max(0,b[j]-i+1))%mod;
}
return f[n+1][0];
}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();m = rd();fac[0] = inv[0] = inv[1] = 1;
for(int i = 2;i < N;i++)inv[i] = (mod-mod/i)*inv[mod%i]%mod;
for(int i = 1;i < N;i++)fac[i] = fac[i-1]*i%mod,(inv[i] *= inv[i-1]) %= mod;
for(int i = 1;i <= n;i++)for(int j = 1;j <= m;j++)
for(int k = rd();k <= 9;k++)a[k][i]++,b[k][j]++;
for(int i = 0;i <= 9;i++)
(ans *= solve(i?a[i-1]:a[10],b[i])*get(a[i],n,m)%mod*get(b[i],m,n)%mod) %= mod;
cout << ans << endl;
return 0;
}
P5115 Check,Check,Check one two
给定一个字符串 S,定义 \(lcp(i,j)\) 表示 \(S[i\ldots n],S[j\ldots n]\) 的最长公共前缀长度,\(lcs(i,j)\) 表示 \(S[1\ldots i],S[1\ldots j]\) 的最长公共后缀长度。你需要求:
\(\sum\limits_{1\leq i < j \leq n}lcp(i,j)lcs[i,j](lcp(i,j)\leq k1)[lcs(i,j) \leq k2]\)
\(n\le 10^5\)
先考虑没有 \(k1,k2\) 的限制。考虑对于一对 \((i,j)\),设 \(p=lcp(i,j)\),对于 \(\forall k\in[0,p]\),我们将 \((i,j)\) 的贡献拆到 \((i+k,j+k)\) 上去,现在贡献就去掉了一个 \(lcp(i,j)\),剩一个 \(lcs(i,j)\)。枚举 SAM 中的每个点,求出有多少对 \(lcs(x,y)=len\),那么对于任意一对 \((x,y)\),它们的贡献是一样的。
现在考虑考虑对于任意一对 \((x,y)\),哪些 \((i,j)\) 会对它们造成贡献。枚举 \(i\in[x-len+1,x],j=y-(x-i)\),那么 \((i,j)\) 造成的贡献为 \(i-x-len+1)+1\),即贡献是从 \(1\) 加到 \(len\) 的等差数列。现在就完成了没有 \(k1,k2\) 限制的部分。如果有 \(k2\),那么就要求等差数列的上限不超过 \(k2\) 即可。
然后考虑 \(k1\) 的限制,我们首先要求等差数列的首项不小于 \(len-k1+1\),然后考虑有哪些 \((i,j)\) 会被计算重复。如果 \(lcp(i,j) > k1\),那么我们在枚举 \((i+k1,j+k1)\) 时减去所有的贡献。
当枚举到一个 \((x,y)\),它被计算重复当且仅当 \(lcp(x,y) > k1,lcs(x,y)\le k2\),此时多算的贡献为 \(lcs(x-k1,y-k1)\times k1\),减掉即可。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#define ll unsigned long long
using namespace std;
const int N = 2e5+5;
char s[N];int n,lst = 1,tot = 1,k1,k2;
ll cnt[N],ans;vector<int> e[N];
struct node{int fa,len,ch[26];}t[N];
void ins(int c)
{
int p = lst,nw = lst = ++tot;
t[nw].len = t[p].len+1;cnt[nw] = 1;
for(;p&&!t[p].ch[c];p = t[p].fa)t[p].ch[c] = nw;
if(!p){t[nw].fa = 1;return ;}
int q = t[p].ch[c];
if(t[q].len == t[p].len+1)t[nw].fa = q;
else
{
int nq = ++tot;t[nq] = t[q];
t[nq].len = t[p].len+1;
t[q].fa = t[nw].fa = nq;
for(;p&&t[p].ch[c]==q;p = t[p].fa)t[p].ch[c] = nq;
}
}
inline ll S(ll l,ll r){return l > r?0:(l+r)*(r-l+1)/2;}
void dfs(int u)
{
ll sum = 0;int len = t[u].len;
for(int v : e[u]){dfs(v);sum += cnt[u]*cnt[v];cnt[u] += cnt[v];}
ans += sum*S(max(1,len-k1+1),min(len,k2));
if(len > k1&&len-k1 <= k2)ans -= sum*(len-k1)*k1;
}
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
scanf("%s",s+1);n = strlen(s+1);
k1 = rd();k2 = rd();
for(int i = 1;i <= n;i++)ins(s[i]-'a');
for(int i = 1;i <= tot;i++)e[t[i].fa].push_back(i);
dfs(1);
cout << ans << endl;
return 0;
}
[AGC037F] Counting of Subarrays
有一个常数 L,称一个序列是 \(k\) 级的当且仅当这个序列只有一个数 \(k\),或者可以划分为 \(\ge L\) 个 \(k-1\) 级的序列。现在给定一个长为 \(n\) 的序列 \(a\),求 \(a\) 有多少个子区间满足,存在一个 \(k\) 使得这个区间是 \(k\) 级的。
\(n\le 2\times 10^5,a_i\le 10^9\)
先考虑怎么判断一个序列是否合法,我们把把操作倒过来做,每次相当于可以选择一段长度 \(\ge L\) 的相同的数 \(x\),把这些数合并成一个数 \(x+1\)。那么最优策略就是每次选择序列中最小值所在段,将这个段尽可能的合并,假设这一段长为 \(x\),如果 \(x < L\),那么就不合法,否则就能合并出 \(\lfloor\frac x L\rfloor\) 个数。一直做下去知道序列中只剩一种数,如果此时序列长度为 \(1\) 或者长度 \(\ge L\) 那么就是合法的。
模拟上述做法,每次相当于用 \(\mathcal{O}(L)\) 的代价将序列长度减少 \(L-1\)。枚举次数为线性。我们特判掉最后区间长度为 \(1\) 的情况,这种情况就相当于最开始只有 \(1\) 个数,有 \(n\) 种。于是现在就是求有多少个子区间合并到只有一种数时区间长度 \(\ge L\)。
我们还是模拟上述过程,每次合并一段区间,然后计算这个区间内有多少个合法的子区间。合并之后,有可能一个合法的子区间的一个端点在合并的点上另一个不在,这个时候这个区间对答案的贡献就不是 \(1\) 了,而应该有一个权重。于是粗略的想,我们可以给每个点赋一个权重,每次合并点时把权重也合并起来,再计算后面的答案。
具体地,我们对每个点赋两个权值 \(l_i,r_i\),一个合法的子区间 \([i,j]\) 对答案的贡献为 \(l_i\times r_j\),初始时 \(l_i=r_i=1\),每次计算一段区间的代价,这个可以直接前缀和优化求出。然后考虑合并,先考虑 \(r_i\) 的合并,假设这一段有 \(m\) 个数,那么合并后有 \(\lfloor\frac m L\rfloor\) 个数。如果有一个合法的子区间以合并后第一个点作为右端点,那么实际上等价于以原来段中位置 \([L,2L-1]\) 作为右端点,相当于第一个点的 \(r_i\) 等于 \([L,2L-1]\) 中的 \(r_i\) 的和。
于是我们就可以得出,原来段中第 \(i\) 个点的 \(r_i\),应该贡献给合并后第 \(\lfloor\frac i L\rfloor\) 个点的 \(r_i\)。左端点同理,就是从左往右数变成了从右往左数。
于是每次我们就可以合并一个段的同时将 \(l,r\) 也合并出来,然后继续计算即可。注意后面计算有可能会统计到左右端点都在当前合并的区间内的情况,我们要将这些减掉。所以每次是找到最小段,然后加上这段的答案,然后合并这段的点和 \(l_i,r_i\),然后再减去合并后这一段的答案,一直重复下去即可。
每次用堆找到一个最小值所在段,然后合并,总复杂度为 \(\mathcal{O}(n\log n)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#include <utility>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 2e5+5;
int a[N],id[N],nex[N],pre[N],n,L;
ll ans;
set<pair<int,int> > s;
struct node{int l,r;}f[N],tmp[N],now[N];
ll calc(node *a,int n)
{
ll ans = 0,sum = 0;
for(int i = L;i <= n;i++)
sum += a[i-L+1].l,ans += a[i].r*sum;
return ans;
}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();L = rd();
for(int i = 0;i <= n+1;i++)nex[i] = i+1,pre[i] = i-1;
for(int i = 1;i <= n;i++)a[i] = rd(),s.insert({a[i],i}),f[i] = {1,1};
while(!s.empty())
{
int x = s.begin()->second,p = 0,y = x;
for(;a[y] == a[x];y = nex[y])
tmp[++p] = f[y],id[p] = y,s.erase({a[y],y});
ans += calc(tmp,p);
int m = p/L;
if(!m){pre[y] = nex[pre[x]] = 0;continue;}
for(int i = 1;i <= m;i++)now[i] = {0,0};
for(int i = 1;i <= p;i++)
now[m-(p-i+1)/L+1].l += tmp[i].l,now[i/L].r += tmp[i].r;
ans -= calc(now,m);
for(int i = 1;i <= m;i++)f[id[i]] = now[i],s.insert({++a[id[i]],id[i]});
nex[id[m]] = y;pre[y] = id[m];
}
cout << ans+n << endl;
return 0;
}
[ARC147F] Again ABC String
\(T\) 组询问,每组给定 \(n,X,Y,Z\),求有多少个长度为 \(n\) 且只由 ABC 构成的字符串满足:设 \(A_i,B_i,C_i\) 分别表示前 \(i\) 个字符中 A,B,C 的个数,需要使得对于每个 \(1\le i\le n\),满足:\(A_i-B_i\le X,B_i-C_i\le Y,C_i-A_i\le Z\)。
答案对 \(2\) 取模。\(T\le 10,n,X,Y,Z\le 10^9\)
我们设有 \(3\) 个变量 \(a,b,c\),分别表示当前的 \(X-(A_i-B_i),Y-(B_i-C_i),Z-(C_i-A_i)\)。初始时三个变量分别为 \(X,Y,Z\),每次填一个 A,就是将 a--,c++,填 B,C 类似,然后要求 \(a,b,c\ge 0\)。我们将所有 \(X,Y,Z\) 加一,于是要求 \(a,b,c > 0\)。
下面是一个非常牛逼的转化,现在有一个长度为 \(m=X+Y+Z\) 的环,有三个点分别在 \(0,X,X+Y\) 的位置,每次操作相当于把某一个点顺时针移动一次,然后要求任何时刻两个点不能到同一个位置,求有多少种移动方案。(相当于两个点间的距离分别为 \(a,b,c\))
考虑容斥,用总方案数减去存在两个时刻有两个点在同一位置的方案数。我们发现,如果有两个时刻两个点到达了同一位置,之后如果有任意一个点移动,那么之后如果这两个点有移动,那么将这两个点的身份互换一定也是一种方案,模 \(2\) 为 \(0\),可以抵消。所以最终如果三个点的位置都不同,那么一定是整个都合法或者中间有两个点碰到一起后其中一个移动了一段距离,这两种情况都不应该计入答案,所以只需要考虑最终状态下有两个点在同一位置的情况。
我们枚举具体是哪两个点最后到了同一位置,将三种情况加起来,如果最终情况是 \(3\) 个点到了同一位置,那么会被计算 \(3\) 次,模 \(2\) 不影响。
现在问题为:在一个长度为 \(m\) 的环上,有两个顺时针方向相距为 \(d\) 的点,每次其中一个点顺时针移动 \(1\),或者两个点不动,求最终两个点位置重合的方案数。列出生成函数,即:
注意 \(i\) 可以是负数。我们首先有个引理:\((x^{-1}+1+x)^{2^k}\equiv x^{-2^k}+1+x^{2^k}\pmod 2\),证明见最下方。
于是将 \(n\) 二进制分解,假设 \(n = \sum 2^{p_i}\),则生成函数可以表示为 \(\prod (2^{-p_i}+1+2^{p_i})\)。于是这就是 \(\log n\) 个多项式循环卷积起来,有了 \(\mathcal{O}(m\log n)\) 的做法。
考虑如果 \(m\) 很大怎么办,这个时候满足 \(i\equiv d\pmod m\) 的 \(i\) 也不多,这个时候我们可以直接枚举所有可能的 \(i\)。具体地,因为负数不方便计算,我们可以所有多项式乘一个 \(2^{p_i}\)。
我们枚举所有满足 \(0\le i\le n,i\equiv d+n\pmod m\) 的 \(i\),求 \(i\) 次项的系数。根据生成函数的意义,这就相当于有一个二进制数,枚举每个 \(j\),每次可以选择给二进数加上 \(2^{p_j}\) 或 \(2^{p_j+1}\) 或 \(0\),求最终有多少种方法能凑出 \(i\)。我们发现所有 \(j\) 互不相同,所以同一个 \(2^{p_j}\) 最多出现两次,于是我们可以直接 dp,设 \(f_{i,0/1}\) 表示当且处理到了第 \(i\) 位,这一位是否有进位,然后转移即可。
我们设一个阈值 \(B = \sqrt{10^9}\),当 \(m\le B\) 时做多项式循环卷积,\(>B\) 时枚举所有 \(i\) 做 dp,复杂度为 \(\mathcal{O}(B\log n)\)。
证:\((x^{-1}+1+x)^{2^k}\equiv x^{-2^k}+1+x^{2^k}\pmod 2\),用三项式将原式展开,即:
\[\sum_{i=0}^{2^k-1}\sum_{j=0}^{2^k-1}x^{i-j}{2^k\choose i}{2^k-i\choose j} \]考虑所有和式中哪些 \({2^k\choose i}{2^k-i\choose j}\ne 0\),根据 Lucas 定理,\({2^k\choose i}\ne 0\) 当且仅当 \(i=0\) 或 \(i=2^k\)。所以只有当 \((i,j)=(0,2^k),(0,0),(2^k,0)\) 时 \(x^{i-j}\) 系数为 \(1\),所以 \((x^{-1}+1+x)^{2^k}\equiv x^{-2^k}+1+x^{2^k}\pmod 2\)。
考拉:\(F(x)^{2^k} \equiv F(x^{2^k})\pmod 2\),其中 \(F(x)\) 是一个关于 \(x\) 的多项式。证明与上面类似。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
bool f[2],g[2];ll n,m;
bool solve(ll x)
{
f[0] = 1;f[1] = 0;
for(int i = 0;i <= 30;i++)
{
for(int o : {0,1})g[o] = f[o],f[o] = 0;
for(int o : {0,1})
for(int j = 0;j <= (n>>i&1)*2;j++)
{
int now = o+(j==1),nex = j==2;
if(now > 1)now -= 2,nex++;
if(now == (x>>i&1))f[nex] ^= g[o];
}
}
return f[0];
}
inline bool calc(ll x){return solve(x+n)^solve(m-x+n);}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
for(int t = rd();t--;)
{
n = rd();ll x = rd()+1,y = rd()+1,z = rd()+1;m = x+y+z;
printf("%d\n",1^calc(x)^calc(y)^calc(z));
}
return 0;
}
[ARC138F] KD Tree
有一个长为 \(n\) 的点列 \((i,p_i)\),\(p\) 是排列,每次可以选择 x/y 和某个坐标将点列分成左右/上下两边(保持两边相对顺序不边),然后分别递归下去,直到区间长度为 \(1\)。求可以得到多少本质不同的点列。
\(n\le 30\)
设 \(f_{l,r,u,d}\) 表示在矩形 \(i\in [l,r],p_i\in [d,u]\) 中的点能构成多少个本质不同的序列,假设里面有 \(m\) 个不同的点。如果直接做就是枚举所有 \(m-1\) 种 x 轴的分割或 y 轴的分割,然后答案加上两侧的答案相乘,但这样显然会有重复。
考虑将一种最终的点列唯一对应到一个划分方案上。我们每次划分时,假设划分分别有 \(X_1,Y_1,X_2,Y_2\ldots X_{m-1},Y_{m-1}\) 这 \(2m-2\) 种方案,那么钦定一个点列对应 \(X_1,Y_1,X_2,Y_2\ldots X_{m-1},Y_{m-1}\) 种第一个能划分出这个点列的划分方法。
于是设 \(f_i\) 表示第 \(i\) 种划分左方/下方的方案数,要求 \(i\) 是最小的可能的划分。那么答案就是所有 \(f_i\) 乘上右方/上方的方案数求和。考虑怎么求 \(f_i\),\(f_i\) 首先等于这种划分左方/下方的方案数,然后要减去所有 \(j<i\) 且划分以 \(j\) 位最小的方案数。
我们枚举 \(j<i\),如果第 \(j\) 种划分的点完全包含于第 \(i\) 种划分的点,那么答案应该减去 \(f_j\) 乘上在 \(i\) 中但不在 \(j\) 中的点的划分方案,这个有点类似有标号连通图计数。
于是就做完了,复杂度为 \(\mathcal{O}(n^6)\),实现时可以用状压设状态,这个复杂度上界远远卡不满。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <ext/pb_ds/assoc_container.hpp>
#define ll long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
using namespace __gnu_pbds;
const int N = 35,mod = 1e9+7;
int p[N],n;
cc_hash_table<int,int> mp;
int dfs(int S)
{
if(!(S&S-1))return 1;
if(mp.find(S) != mp.end())return mp[S];
vector<int> a,b,g;
for(int i = 0;i < n;i++)if(S>>i&1)a.push_back(i),b.push_back(i);
sort(b.begin(),b.end(),[](int x,int y){return p[x] < p[y];});
int m = a.size(),s1 = 0,s2 = 0;ll ans = 0;
for(int i = 0;i < m-1;i++)
g.push_back(s1 |= 1<<a[i]),g.push_back(s2 |= 1<<b[i]);
m = g.size();vector<ll> f(m,0);
for(int i = 0;i < m;i++)
{
f[i] = dfs(g[i]);
for(int j = 0;j < i;j++)
if((g[i]&g[j]) == g[j])(f[i] -= f[j]*dfs(g[i]^g[j])) %= mod;
(f[i] += mod) %= mod;
(ans += f[i]*dfs(S^g[i])) %= mod;
}
return mp[S] = ans;
}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = rd();
for(int i = 0;i < n;i++)p[i] = rd()-1;
cout << dfs((1ll<<n)-1);
return 0;
}
CF1984H Tower Capturing
给定二维平面上的 \(n\) 个点 \((x_i,y_i)\),保证没有任意两点重合、没有任意三点共线、没有任意四点共圆。初始时,你拥有点 \(1\) 和点 \(2\),剩下 \(n−2\) 个点是未拥有的。
每次操作可以选择三个不同的点 \(P,Q,R\),需要满足你拥有点 \(P,Q\),未拥有点 \(R\),且所有的 \(n\) 个点都在 \(\triangle PQR\) 的外接圆。然后你拥有了 \(\triangle PQR\) 内的还未拥有的点(包括点 \(R\))。
问有多少种不同的操作序列能够让你拥有所有点。两个操作序列不同当且仅当它们的长度不同,或某一步操作选择的无序三元组 \((P,Q,R)\) 不同。\(T\le 10,n\le 100\)
首先三个点的外接圆能包含 \(n\) 个点,这三个点肯定在凸包上。对于给定的两个点,我们要找第三个点使得外接圆包含所有点,那么对于这两个点同一侧的点,肯定只有和这两个点夹角最小的那个点才有可能成为答案,对于另一侧同理。于是对于一开始的两个点,我们最多找到两个不交的三角形。
找到之后可以递归下去,我们发现之后的划分中每次选择的两个点,一定是有连边的两个点。于是一直划分一下去,所有三角形相当于构成了一个凸包的三角剖分。这个划分是一个树形结构,答案就是树的拓扑序计数。
我们每次递归时可以暴力找第三个点,看这三个点的外接圆是否包含所有点,如果是就递归下去。如果两边都可以划分,那么答案就是两边的划分的方案的乘积再乘上一个组合数。总时间复杂度 \(\mathcal{O}(Tn^3)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define double long double
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
const int N = 105,mod = 998244353;
const double eps = 1e-5;
int n;ll C[N][N];
struct node
{
int x;ll y;
friend node operator + (const node &x,const node &y)
{return {x.x+y.x,x.y*y.y%mod*C[x.x+y.x][x.x]%mod};}
};
struct point{double x,y;}a[N];
struct line{double a,b,c;}f,g;
inline double dis(point x,point y)
{return (x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y);}
inline line get(point x,point y)
{
double mx = (x.x+y.x)/2,my = (x.y+y.y)/2,A = x.x-y.x,B = x.y-y.y;
return {A,B,-A*mx-B*my};
}
inline point calc(line f,line g)
{return {(g.c*f.b-f.c*g.b)/(f.a*g.b-f.b*g.a),(g.c*f.a-f.c*g.a)/(f.b*g.a-f.a*g.b)};}
bool check(point x,double d)
{
for(int i = 1;i <= n;i++)
if(dis(x,a[i]) > d+eps)return 0;
return 1;
}
node dfs(int x,int y,int fa)
{
node ans = {0,1};
for(int i = 1;i <= n;i++)if(i != x&&i != y&&i != fa)
{
point p = calc(get(a[x],a[i]),get(a[y],a[i]));
if(check(p,dis(a[i],p)))
{
node g = dfs(x,i,y)+dfs(y,i,x);
g.x++;ans = ans+g;
}
}
return ans;
}
char buf[1<<21],*p1,*p2;
inline int rd()
{
char c;int f = 1;
while(!isdigit(c = getchar()))if(c=='-')f = -1;
int x = c-'0';
while(isdigit(c = getchar()))x = x*10+(c^48);
return x*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
for(int i = 0;i < N;i++)for(int j = C[i][0] = 1;j <= i;j++)
C[i][j] = (C[i-1][j-1]+C[i-1][j])%mod;
for(int t = rd();t--;)
{
n = rd();
for(int i = 1;i <= n;i++)a[i] = {rd()*1.0,rd()*1.0};
node ans = dfs(1,2,0);
printf("%lld\n",(ans.x>0)*ans.y);
}
return 0;
}
[AGC050F] NAND Tree
给定一棵 \(n\) 个点的数,每个点有点权 \(0/1\),定义一次操作为:
- 选择一条边,将这条边的两个端点合并,新点的点权为原来两个点权的 \(\operatorname{NAND}\)(\(\operatorname{NAND}(x,y) = \neg(x\and y)\))。
\(n-1\) 次后树会只剩下一个节点。求在 \((n-1)!\) 种操作顺序中,最终剩下的点的点权 \(1\) 的方案数,答案对 \(2\) 取模。
\(n\le 300\)
神仙题。
考虑利用 \(\bmod 2\) 的性质,如果我们某两次操作的两条边没有公共点,那么交换这两次操作对答案是没有影响的,所以可以抵消掉。于是我们将所有操作两两分组,要求每组内的两次操作必须有公共点,即第 \(2i-1\) 次操作和第 \(2i\) 次操作必须有公共点,如果 \(n\) 是偶数,我们就枚举第一次操作的边使得操作数是偶数。
对于某两次操作,因为有公共点,所以可以写成 \(x-y-z\) 的样子。如果 \(a_x=a_z\),那么两次操作交换后不影响答案,可以抵消。如果 \(a_x\ne a_z\),可以发现两次操作交换和不交换得到的结果一定是 \(0\) 和 \(1\),这是因为 \(\operatorname{NAND}(\operatorname{NAND}(y,x),z) = x\)。于是我们可以每次选择两个操作(不考虑操作间的顺序)进行合并,要求 \(a_x\ne a_z\),然后将 \(x,y,z\) 缩成一个自由点,自由点表示这个点取 \(0/1\) 时都是一种方案。
接下来考虑有自由点参与的合并,可以发现,如果 \(y\) 是自由点那么一定会抵消,如果 \(x,z\) 都是自由点,那么也抵消了!所以如果有自由点参与合并,那么一定是在 \(x\) 或 \(z\) 并且另一个点不是自由点,而且合并后 \(x,y,z\) 又会缩成一个自由点。那么如果树上已经有一个自由点了,又合并出了一个新的自由点,则最终这两个自由点一定会相遇,那么贡献一定为 \(0\)。
所以我们一定只会在第一次操作时合并出一个自由点,之后每次操作都是这个自由点作为 \(x\) 或 \(z\) 参与合并。那么在最终只剩一个点时,这个点一定是自由点,取 \(1\) 时就是一种方案。于是问题就变成了,有多少种方案满足,一开始选择三个点进行合并,之后每次选择包含上次合并出来的点的三个点进行合并。
可以发现这相当于是一个每次选择两个点的拓扑序计数,把开始三个点也算上,那么就是求有多少个拓扑序 \(c_1,\ldots,c_n\),满足所有 \(c_{2i-1}\) 都是 \(c_{2i}\) 的父亲。开始三个点还要求 \(a_x\ne a_z\),为了防止记重,我们还要钦定 \(a_{c_1} = 1,a_{c_3} = 0\)。然后如果你注意力惊人,可以发现 \(a_{c_3}=0\) 和 \(c_{2i-1}\) 是 \(c_{2i}\) 的父亲这两个条件都可以忽略,即只需要以所有 \(a_u=1\) 的点作为根进行拓扑序计数再求和即可。
为什么这是对的,先考虑 \(c_{2i-1}\) 是 \(c_{2i}\) 的父亲这个条件,如果某个拓扑序存在 \(i\) 不满足这个条件,那么我们可以找到第一个 \(i\),则交换 \(c_{2i-1}\) 和 \(c_{2i}\) 依然合法,所以可以抵消。再考虑 \(a_{c_3} = 0\) 这个条件,如果 \(a_{c_3} = 1\),那么在以 \(c_1,c_3\) 为根时都会计算一遍,也会抵消。
所以直接对每个 \(a_u=1\) 的点为根做拓扑序计数即可,因为拓扑序个数为 \(\frac{n!}{\prod siz_u!}\),所以我们求出所有 \(x!\) 中 \(2\) 的因子个数即可。算上一开始的枚举第一次操作,总复杂度为 \(\mathcal{O}(n^3)\)。当然简单换根可以做到 \(\mathcal{O}(n^2)\)。
Submission #65342675 - AtCoder Grand Contest 050 (Good Bye rng_58 Day 1)
[AGC028E] High Elements
给定一个 \(1\sim n\) 的排列 \(p\),求一个字典序最小的 01 串 \(s\),满足:将 \(s\) 中 0 在 \(p\) 中对应下标的数和 1 对应的数分别拉出来构成两个序列,这两个序列的 \(premax\) 个数相等。或者报告无解。
\(n\le 2\times 10^5\)
因为要字典序最小,所以考虑逐位确定,每次相当于给定一个前缀的划分方式,求是否存在后面的划分方式满足条件。假设前面已经分成了两个序列 \(a,b\),设这两个序列的 \(premax\) 个数分别为 \(c_a,c_b\),最大值分别为 \(h_a,h_b\)。后面的全局 \(premax\) 个数为 \(s\),这 \(s\) 个数一定会造成贡献,剩下的一些非 \(premax\) 的数可能会造成贡献。
可以发现,一个非 \(premax\) 的位置放在它前一个 \(premax\) 所在序列中贡献为 \(0\),那么如果剩下的非 \(premax\) 位置对 \(a,b\) 序列都有贡献,那么可以交换两个对 \(a,b\) 有贡献的非 \(premax\) 位置,这样两边答案都减 \(1\)。一直调整下去,一定存在一边全是由 \(premax\) 造成贡献,不妨设是 \(a\) 数组。假设 \(b\) 数组中有 \(k\) 个全局 \(premax\),有 \(m\) 个非 \(premax\) 有贡献,那么有等式:
移项得 \(2k+m = c_a+s-c_b\),右边部分是一个常数。于是我们可以将 \(premax\) 赋权值 \(2\),非 \(premax\) 位置赋权值 \(1\),那么就相当于在后面选一个权值和恰好为 \(c_a+s-c_b\) 的上升子序列,并且开头要大于 \(h_b\)。由于权值只有 \(1,2\),所以如果有一个权值和为 \(x\) 的上升子序列,那么一定存在和为 \(x-2\) 的上升子序列,所以我们只需要求所有权值和为奇数或偶数的上升子序列中权值和最大是多少。
于是我们先用两棵线段树维护出整个序列中以 \(>x\) 的数开头,并且权值和为奇数/偶数的上升子序列中权值和最大是多少,然后每次删去当前的数,就可以查询这个后缀的答案,相当于单点修改,区间查 \(\max\)。复杂度为 \(\mathcal{O}(n\log n)\)。
[AGC014F] Strange Sorting
给定一个 \(1\sim n\) 的排列 \(p\),定义一次操作为将排列中所有 \(premax\) 按原来顺序移到排列末尾,求经过多少次操作后 \(p\) 会变得有序。
\(n\le 2\times 10^5\)。
可以发现 \(1\) 这个数对 \(premax\) 没有影响,假设我们先求出了排列去除 \(1\) 的答案,考虑求出加上 \(1\) 后的贡献。如果我们能处理这个子问题,那么就可以依次枚举 \(i\) 从 \(n\) 到 \(1\),然后求出 \(i\) 对 \([i+1,n]\) 的子序列的贡献,求和即可。
假设 \([2,n]\) 的答案是 \(t\),如果 \(t=0\),那么就是看 \(1\) 是否在整个序列的开头,如果不是那么就会执行一次操作。
否则,我们设 \(f\) 表示 \([2,n]\) 在最后一次操作时序列开头是多少,显然有 \(f > 2\),因为如果 \(f = 2\),那么最后一次操作一定会让 \(2\) 移到非开头位置,此时肯定没有排好序。那么最后一次操作时,\(1,2,f\) 的相对位置可能有 \((1,f,2),(f,1,2),(f,2,1)\),如果是 \((f,1,2)\) 那么最后一次操作 \(1\) 也会排好,其余两种情况则会多排一轮。
现在问题就是如何判断最后一次操作时 \((1,2,f)\) 的相对关系,可以发现 \((1,f,2),(f,2,1)\) 都会有 \(1\) 的贡献,而 \((f,1,2)\) 没有贡献,即与 \((1,f,2)\) 循环同构即会有贡献,否则就没有。那么我们可以大胆猜测任何一次操作都不会改变 \((1,2,f)\) 的循环同构顺序,那么只需要判断最开始排列 \((1,2,f)\) 的顺序即可。人类如何想出这一步?
考虑证明上述结论,首先有一个结论是 \(f\) 除了最后一次操作其余时刻一定不会被操作(即不是 \(premax\)),因为如果被操作了那么 \(f\) 前一定会有个 \(<f\) 的数,那么之后 \(f\) 一定不会成为开头。可以直接枚举 \((1,2,f)\) 的 \(6\) 种全排列考虑:
- 如果相对顺序为 \((f,1,2)\) 或 \((f,2,1)\),因为 \(f\) 不是 \(premax\),所以 \(1,2\) 也不是,即所有数都不会被操作。
- 如果相对顺序为 \((1,f,2)\) 或 \((2,f,1)\),那么后两个数不是 \(premax\),无论第一个数是否是 \(premax\) 都不会改变循环同构。
- 如果相对顺序为 \((1,2,f)\) 或 \((2,1,f)\),可以发现当第二个数是 \(premax\) 时第一个数一定是 \(premax\),也都不会改变循环同构。
综上,我们可以直接用一开始 \((1,2,f)\) 的顺序来确定是否有贡献,于是直接枚举 \(i\) 从 \(n\) 到 \(1\),记录此时的 \(t,f\) 即可。复杂度 \(\mathcal{O}(n)\)。
Submission #65361743 - AtCoder Grand Contest 014
[ARC206E] Rectangle Coloring
给定一个 \(n\times n\) 的棋盘,称在棋盘边上但不在角落上的格子为好格子,给定每个好格子的权值(共 \(4n-8\) 个)。初始时所有格子都是白色,定义一次操作为:
- 选择两个不同的未被选择过的好格子,然后将这两个格子确定的矩形染黑,代价为这两个格子的权值之和。
求将所有格子染黑的最小代价。
\(4\le n\le 5\times 10^4\)
场切,爽
因为每次操作至多覆盖一个角落,所以我们至少需要 \(4\) 次操作,每条边至少需要选两个格子。那第一想法就是每条边选权值最小的两个格子,考虑什么情况下不合法,如下图:
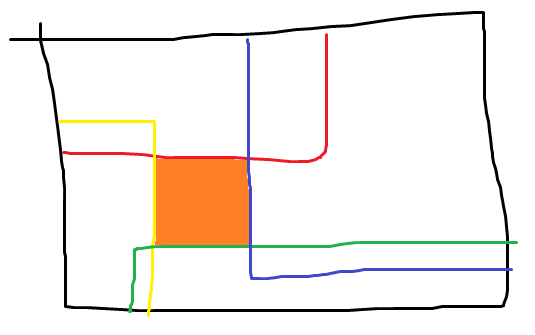
(橙色格子是没有被覆盖到的,这张图对称的情况也不合法)
于是我们先考虑所有每条边选 \(8\) 个点的合法情况的最小值。然后考虑选了 \(>8\) 个点的情况,那么就相较于上图,就要至少再增加两个点,显然这两个点不能在同一条边上,而如果增加到邻边上使得矩阵被覆盖完了,那么一定可以删掉两个点,于是这种情况不优。
最后还有可能加两个点到对边上,可以发现无论这两个点加到哪,都一定可以覆盖完整个矩阵,所以答案就是对边前 \(3\) 小值+另一组对边前 \(2\) 小值。两种情况都可以简单计算,总复杂度为 \(\mathcal{O}(n)\)。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号