数值优化（十）

最小二乘方

在最小二乘方问题中，目标函数有如下的形式$$f(x)=\frac{1}{2} \sum_{j=1}^{m}r2_j(x)$$针对这种特殊的形式，可以采取专门的方法来加速优化。计算其梯度以及Hessian得到$$\nabla f(x) = \sum_{j=1}^m r_j(x)\nabla r_j(x) = J(x)^T r(x)$$$$\nabla^2 f(x) =J(x)^{TJ(x)+\sum_{j=1}}m r_j(x) \nabla^2 r_j(x)$$其中第二项往往很小，因为在实际问题中，用最小二乘法来确定参数，\(r_j\)代表预测值与真实值的差，这应该是很小的，又由于解附近的near-linearity性质导致二次导数很小，于是有$$\nabla^2 f(x) \approx J(x)^TJ(x)$$这一点是经常被利用到的。

Gauss-Newton

Gauss-Newton在Newton法上做了一些改进，Newton法需要通过$$\nabla^2 f_k p_k =-\nabla f_k $$计算出优化方向\(p_k\)，现在直接把上面得到的估计式代入，得到GN方向\(p_k^{GN}\)满足$$J_k^TJ_kp_k=-J_k^Tr_k$$由于求梯度的时候就已经计算了\(J\)，所以第二步完全省略了Hessian矩阵的计算时间，接下来就可以按正常的步骤选择优化步长。

Levenberg-Marquardt

L-M方法就是改进后的信任域方法，仍然是利用二乘方问题独有的Hessian估计，在迭代点求解$$m_k = \frac{1}{2}|r_k|^2+pTJ_k^{Tr_k+\frac{1}{2}p}TJ_k^TJ_kp \quad |p|\leq \Delta_k$$即$$m_k = \frac{1}{2} \J_kp+r_k||_2^2 \quad |p| \leq \Delta_k$$

正交距离回归

正交距离回归是在回归问题中不仅考虑到因变量的误差，还考虑到自变量的测量误差而得到的优化问题，目标函数有如下形式$$f(x) = \frac{1}{2}\sum_{j=1}^m w_j^2 \epsilon_j^2 +d^2_j \delta_j^2$$其中\(d_j\)是常数权重并且$$y_j =\Phi(x;t_j+\delta_j)+\epsilon_j$$正交距离回归示意图如下

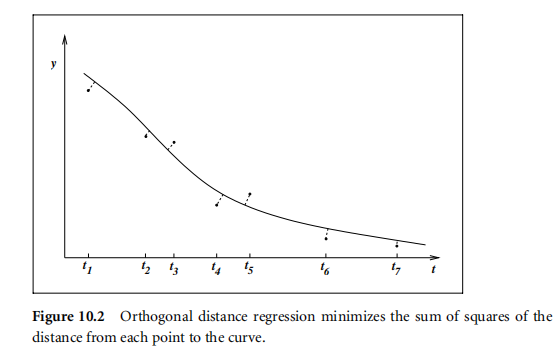
这个目标函数也可以整理成普通二乘方目标函数的形式


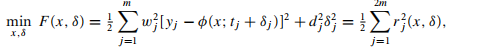
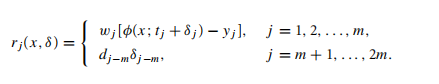
然而规模似乎大了一倍，幸运的是，它的Jacobian有特殊的形式

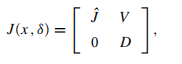
\(\hat{J}\)是\(w_j \Phi(t_j+\delta_j;x)\)的Jacobian，V，D是对角阵