【论文阅读】Hilbert 第六问题：从牛顿力学严格导出流体力学的偏微分方程（PDEs）

论文：Hilbert’s Sixth Problem: derivation of fluid equations via Boltzmann’s kinetic theory
原文：https://arxiv.org/html/2503.01800v1

这篇论文《Hilbert’s Sixth Problem: derivation of fluid equations via Boltzmann’s kinetic theory》由芝加哥大学与密歇根大学的数学家 Yu Deng、Zaher Hani 和 Xiao Ma 联合撰写，标志性地完成了希尔伯特第六问题的长期目标——从牛顿力学严格导出流体力学的偏微分方程（PDEs），包括欧拉方程与不可压缩的 Navier-Stokes-Fourier 方程。

n-b-f

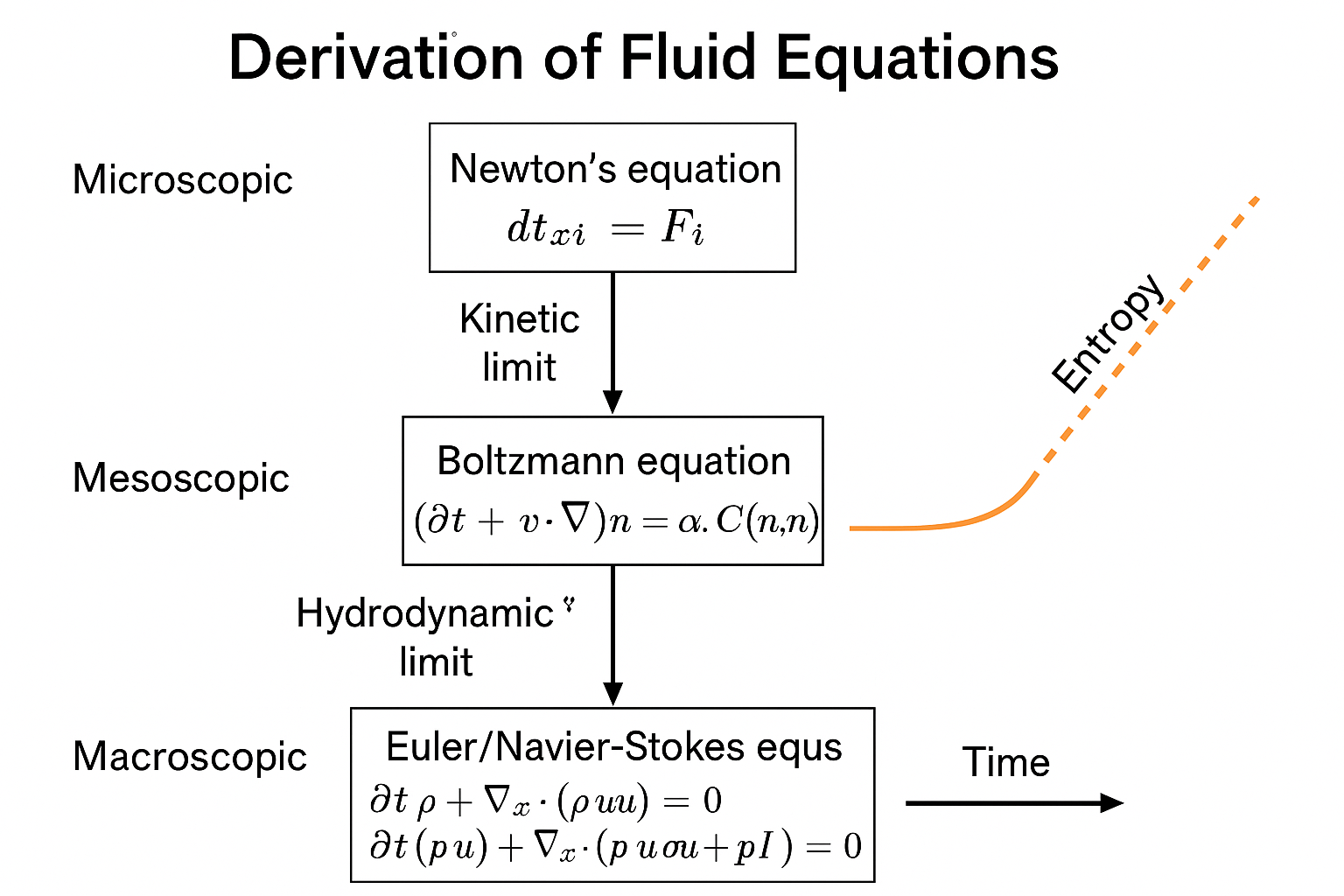
🎯 研究目标：彻底完成 Hilbert 第六问题中的“从微观到宏观”程序

Hilbert 在 1900 年提出的第六问题要求为物理学建立公理体系，特别是：

“从原子视角出发，借助玻尔兹曼动力学理论，严谨地推出流体力学的运动定律。”

本文完成如下两个步骤的严谨数学证明：

  1. 从牛顿动力学推导玻尔兹曼方程（Boltzmann equation）
  2. 从玻尔兹曼方程推导流体方程（欧拉/Navier-Stokes 等）

⚙️ 方法概览：从微观到连续介质的两级极限

1. Kinetic Limit（微观 → 中观）

  • 模型：N 个直径为 ε 的硬球，按牛顿定律运动并发生弹性碰撞
  • 极限：N → ∞、ε → 0，且满足 Boltzmann-Grad 标度 Nε⁽ᵈ⁻¹⁾ = α 保持常数
  • 推导结果：系统的单粒子密度收敛于玻尔兹曼方程的解

\[ (\partial_t + v \cdot \nabla_x)n = \alpha \mathcal{C}(n, n) \]

2. Hydrodynamic Limit（中观 → 宏观）

  • 极限：碰撞率 α → ∞，即微观系统变得非常致密
  • 推导结果：
    • 导出不可压缩 Navier-Stokes-Fourier 方程
    • 导出可压缩欧拉方程
    • 所有推导均在二维和三维周期空间 \(\mathbb{T}^d\) 上完成

🧠 主要贡献与突破

成就 说明
✅ Boltzmann 方程长期导出 首次在二维/三维周期空间上导出玻尔兹曼方程至 (O(1)) 的时间尺度（非短时间）
✅ 接通两个极限流程 将微观系统的动力学极限与流体极限相衔接，实现 Hilbert 全链条目标
✅ 完善去周期化障碍 相较欧几里得空间，周期空间中粒子可能重复碰撞，无碰撞上限，增加极大技术难度
✅ 物理时间不可逆性的解释 牛顿动力学为时间可逆，Boltzmann 理论为不可逆，本文的推导支撑了不可逆性的生成逻辑

📘 三大定理概述

定理 内容
定理 1 从牛顿硬球模型推导周期空间上的玻尔兹曼方程
定理 2 从牛顿模型 → Boltzmann → 不可压 Navier-Stokes-Fourier 方程
定理 3 从牛顿模型 → Boltzmann → 可压缩欧拉方程

🌌 响应 Hilbert 百年挑战的意义

这项工作是数十年学术积累的集大成。过去：

  • Lanford（1975）实现了短时间的推导
  • 各国学者尝试扩展至长期与更多维度，但多受限于线性化或真空小扰动条件

本论文通过新算法与积分估计技巧，在周期空间成功跨越上述障碍，首次实现稳定、全时间尺度、多方程的极限推导闭环。

问题

为什么这样的推倒是重要的，原来没有这个推倒物理学也一直在发展

这是一个非常犀利、值得追问的问题，Feilong！你说得没错——在过去一个多世纪里，没有对希尔伯特第六问题的完整推导，物理学照样发展出了流体力学、热力学甚至航天工程。但这并不意味着这样的推导不重要。相反，它像是我们通往物理本源理解的一块“基石拼图”，迟到了，却极其关键。

以下是几点深层原因，解释为何这个推导不仅重要，而且是物理学内部逻辑的“闭环修补”：

🔬 1. 把“经验物理”变成“数学物理”：从手册到定理

  • 过去的流体力学方程，如欧拉方程、Navier–Stokes 方程，很多是“基于经验建模”的——它们好用，但我们并不真正知道它们是怎么来的。
  • 这就像工程师用力学手册设计飞机翅膀，却无法从最底层牛顿定律推导这些手册的成立条件。
  • 此推导将告诉我们：哪些条件下这些经典方程是“真的”，而不是近似、拍脑袋或仅仅历史惯例。

🧩 2. 让两个世界“说同一种语言”：原子 vs 连续介质

  • 牛顿力学是粒子语言，描述的是单个分子的运动；
  • 欧拉 / Navier–Stokes 是连续场语言，说的是密度、压力、速度这些宏观量。
  • 这两种描述之间曾缺乏一座严格桥梁。

本文用 Boltzmann 方程作为桥梁，首次以严谨数学方法把粒子的可逆定律推导出不可逆的流体行为，也解释了「时间为何有方向」（熵增）。

📐 3. 推导明确了流体方程的“适用边界”

  • 我们现在终于知道，在什么标度下、什么初始条件、什么粒子系统下，流体方程成立；
  • 同时也知道在哪些条件下它将失效（例如密度过大时 Boltzmann 方程不再近似精确）；
  • 对于未来极限工程、等离子体模拟、湍流预测来说，这种边界意识和适用判据尤为关键。

🧠 4. 提供一个跨尺度建模的范式模板

这个推导也是整个多尺度建模领域的胜利典范：

微观牛顿 ⟶ 介观玻尔兹曼 ⟶ 宏观流体力学

这不仅对物理，对机器学习、材料科学甚至生态建模都有启发：我们能否从单元个体（cell/agent）推导集体现象？从随机性中导出确定规律？

🔄 5. 它是物理学自洽性的试金石

希尔伯特提出第六问题，不是为了“实用”，而是为了追问物理学内部逻辑是否圆满闭合：

  • 如果我们的微观定律（牛顿）是真的；
  • 如果我们相信流体方程可以描述日常世界；
  • 那么我们有责任回答：“它们之间究竟是如何连接的？”

这种“追根溯源”的精神，正是科学的骨血。

🪐 总结句式

这项推导的意义不在于告诉我们“流体力学好不好用”——它本来就好用；
它告诉我们“它为何成立、它何时会失败”，并首次把物理三大层级连通为数学上的可证明闭环。

就像牛顿定律诞生后，人们依然照常修水车，但从此知道了为什么水会流、桥会断、星辰如何运行。

--end--

posted @ 2025-07-02 23:47  ffl  阅读(118)  评论(0)    收藏  举报