先验、后验、似然

x：观测到的样本。θ：概率模型的参数。

 

先验p(θ)：对参数的各种取值的似然先入为主的判断

后验p(θ|x)：给定样本后，对参数各种取值的似然做出的判断

似然p(x|θ)：给定样本下，参数为真实值的可能性。或者，模糊地讲：参数与样本的匹配程度。

 

 

每一个样本集，对应着的模型，中的参数，的真实值，都记载在上帝的记事本中。观测到样本后，我们估计出的参数与真实值的接近程度，就是似然。

 

我们如何得知自己计算出的参数与真实值的接近程度？

首先我们要确定模型，例如正态分布，θ={μ，σ^2}

 

可以这样想，如果我们得到的参数是真实值，那么在我们的参数下，样本出现的概率应该是最高的。也就是在p(x|θ)，这个式子中，首先我们应注意：x是确定的观测值。我们用不同的θ进行计算，如果θ是真实值的话，算出来的p应该是所有结果中最大的。

 

 

 

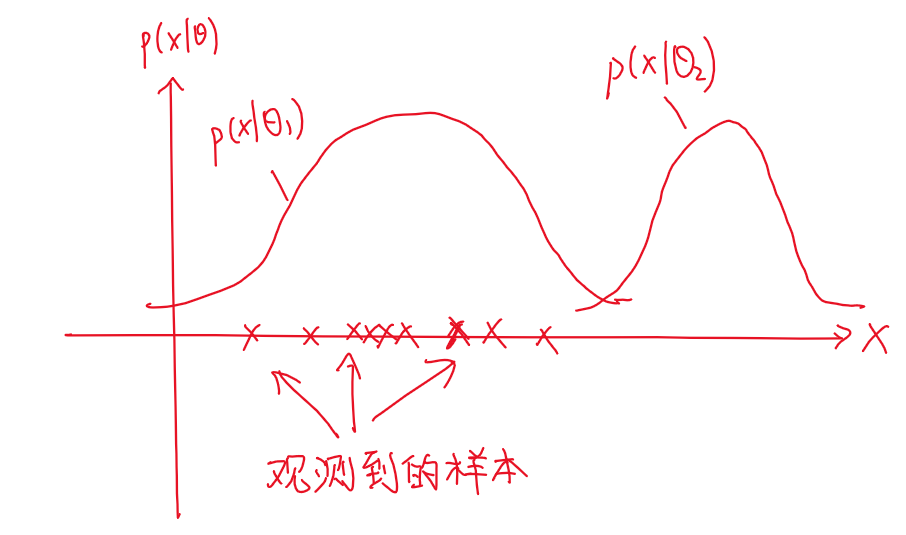
 如图所示，对于两个确定的θ，θ1和θ2，我们代入正态分布的式子，得到上图两条曲线，发现在θ1的条件下，样本对应的概率更高，也就是说，现世观察到的样本和θ1这个参数更加匹配。θ1，更有可能接近神的笔记本上的那个真正的θ。此时，“似然”p(x|θ1)恰大于“似然”p(x|θ2)，这也与前面说的“似然：”那里相呼应。