摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2019/05/11 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2019/03/20 Introduction一定要好好写，写好后要至少读一遍，保证流畅。editor会读introduction来判断是否拒稿。而后文的具体数学内容是referee们判断是否拒稿的主要依据。 当还未给出 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2018/08/08 eikonal equation如下：$$|\nabla_x \tau (x)| = n(x).$$ 定义Hamiltonian：$H(p,x) = \tfrac 1 2 n^{-2}(x)|p|^ 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2018/07/15 常数C： the specific value of C is not required but should be clear from the surrounding context. C ma 阅读全文

摘要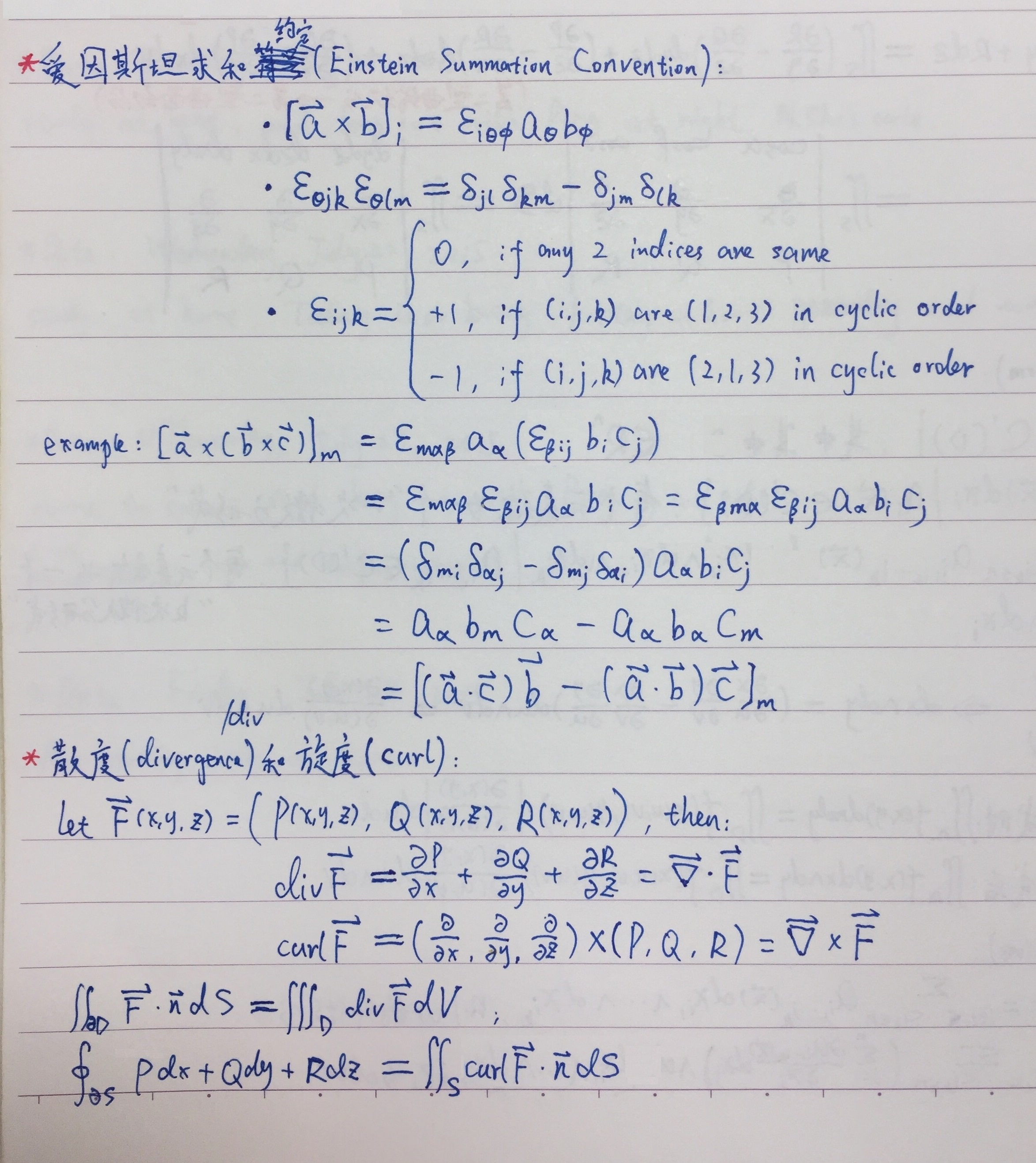： 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2017/06/25 设$A$是$n$维线性空间$V$上的线性变换，它的特征值与相应的代数重数分别为$\lambda_i,m_i~(1=1,\cdots,r)$。为简化阅读，我们设$K_i = \ker(\lambda_ 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2017/06/16 函数定义及前后文详见《Inverse Acoustic and Electromagnetic Scattering Theory》byColton & Kress第三版的公式(5.22) 左右。 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2017/06/16 适合于自己的关于Jacobi-Anger expansion的推导方法，这里记下来，方便以后查阅。 现记住下面四个关系式： \begin{align*} & (1)~ |x-y|=|x| -\hat 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2017/04/15 1、$\text{p.v.}\,\frac{1}{x}$ 因为$(x \ln x - x)' = \ln x$， 所以$\int_0^a \ln x \mathrm{\,d}x = \lim_{\e 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2017/03/30 1、三角函数n次方的定积分值 令$I_n = \int_0^{\pi/2} \sin^n(x) \,\mathrm{d}x = \int_0^{\pi/2} \cos^n(x) \,\mathrm{ 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2017/02/22 将$D^{\alpha}$和$\partial^{\alpha}$区别对待。$D^{\alpha} \overset{\Delta}{=} (-i)^{|\alpha|} \partial^{\al 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2017/02/20 在$\mathcal{D}(0,1)$上取定$\varphi_0 \in \mathcal{D}(0,1)$满足$\int_0^1 \varphi_0(x) \mathrm{d}x = 1$。令$$ 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2017/02/16 Minkowski不等式： 设$f$是$\mathbb{R}^n \times \mathbb{R}^n$上的Lebesgue可测函数，则对任意$1 \leq p < +\infty$，有$$\le 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2016/12/15 为了方便随时查阅，将格林公式贴在此。 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2016/12/12 高中物理书：链接。 以下会用高中的物理知识和大学微积分的数学知识对麦克斯韦方程组进行一个简单的解释。希望大家都能看得懂Maxwell's equations大概说了什么。至少了解个大概吧。 1、高斯 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2016/11/21 有一道题是证明$(\mathbb{R}^n,\|\cdot\|_p)$当$p : 1< p <+\infty$时是uniformly convex的。这个题当然可以用Clarkson定理证明出来。可 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2015/09/08 Today we focus on the following equation:$$u''=au, \textrm{where} (a > 0)$$Due to $a > 0$, $(u'-\sq 阅读全文

摘要：woodbury matrix identity 2014/6/20 【转载请注明出处】http://www.cnblogs.com/mashiqi http://en.wikipedia.org/wiki/Woodbury_matrix_identity Today I'm going to wr 阅读全文

摘要：【转载请注明出处】http://www.cnblogs.com/mashiqi 2014/5/18 以下想法纯属个人的体会，肯定有很多不周到的地方，欢迎大家指正！ 变分思想的源头：引入一个实数，于是可将不好处理的”泛函对函数求导“问题转化为稍微可以下手的”函数对实数求导“的问题。这样的转化得以进行， 阅读全文

摘要：第一个公式： 这个公式的证明需要用到 第二个公式： 证明如下： \[\begin{array}{l}\left| {{I_{p \times p}} + {C_{p \times n}}A_{n \times n}^{ - 1}{B_{n \times p}}} \right| = \left| { 阅读全文