梯度下降入门案例 —— 寻找一元二次方程的极值点

简介

梯度下降(Gradient Descent) 是机器学习中用于优化问题的一种算法，特别是在训练机器学习模型时寻找损失函数的最小值。
“梯度”指的是损失函数对模型参数的偏导数，它表示损失函数在参数空间中增长最快的方向。
“下降”则意味着我们要朝梯度的相反方向更新参数，以此来减少损失。

本案例中，目标方程为： $ f(x) = (x - 3.5)^2 - 4.5x + 10 $ ，图案是开口朝上的抛物线，易得其导数： $ \nabla g(x) = 2(x - 3.5) - 4.5 $

求解方法

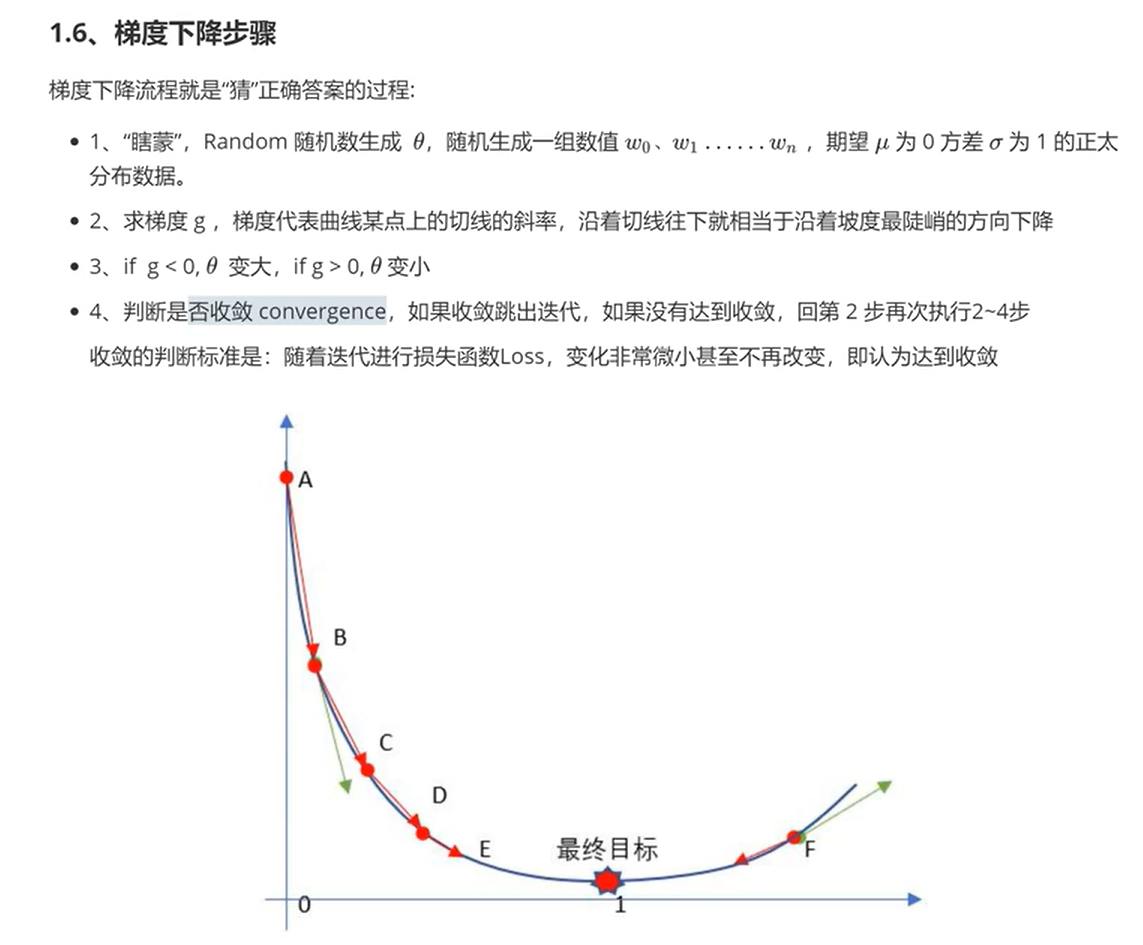
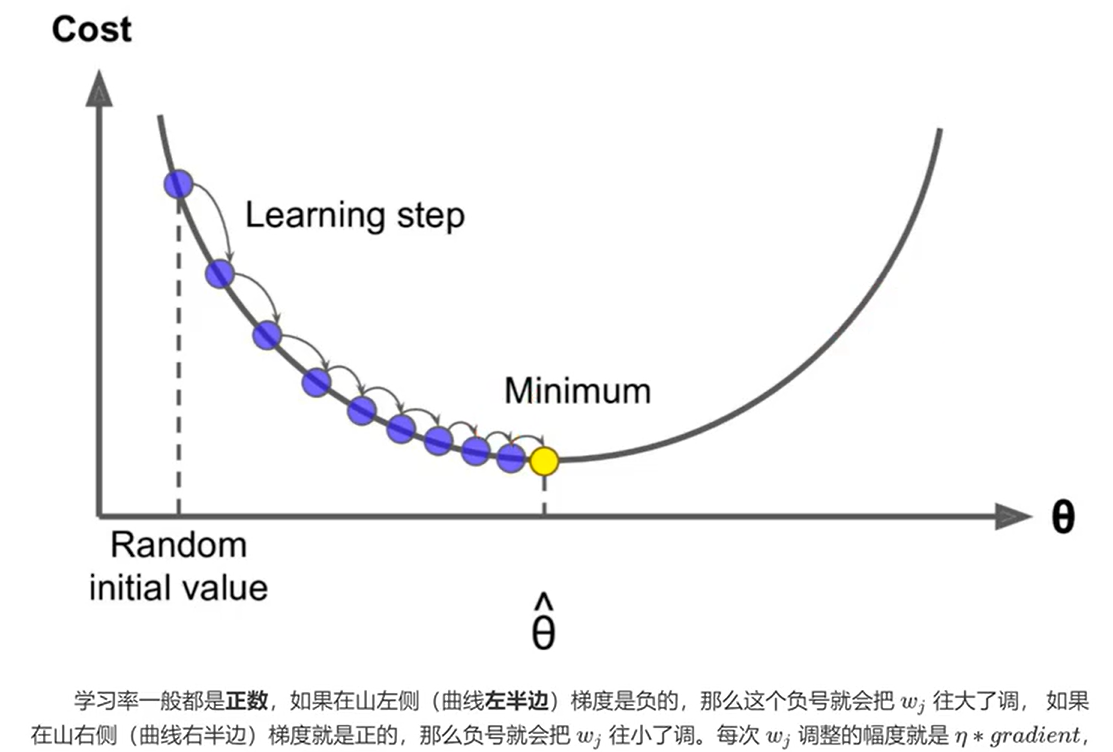
首先，随机生成一个在函数区间内的横坐标，记为 \(x\)，并根据其导数 \(\nabla g(x)\) 的方向，选择梯度下降的一端移动，移动的距离与学习率 \(\eta\) 和导数值 \(\nabla g(x)\) 有关，得到新的横坐标 \(x\)，重复上述步骤，直到每次移动的距离小于目标精度。

下方补充三张图，作为求解方法的具体描述

运行结果

1. 学习率适中 (eta = 0.3)

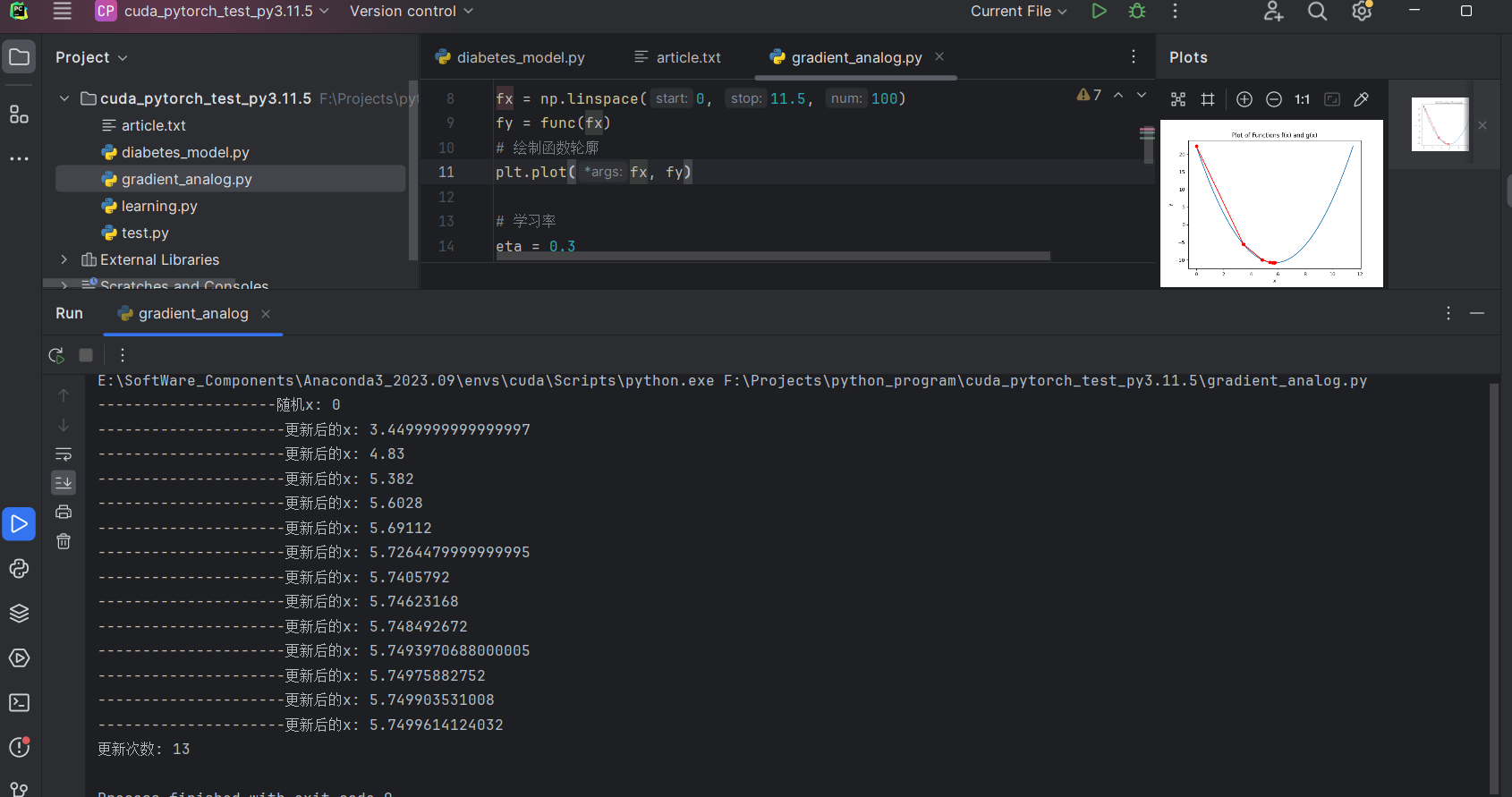
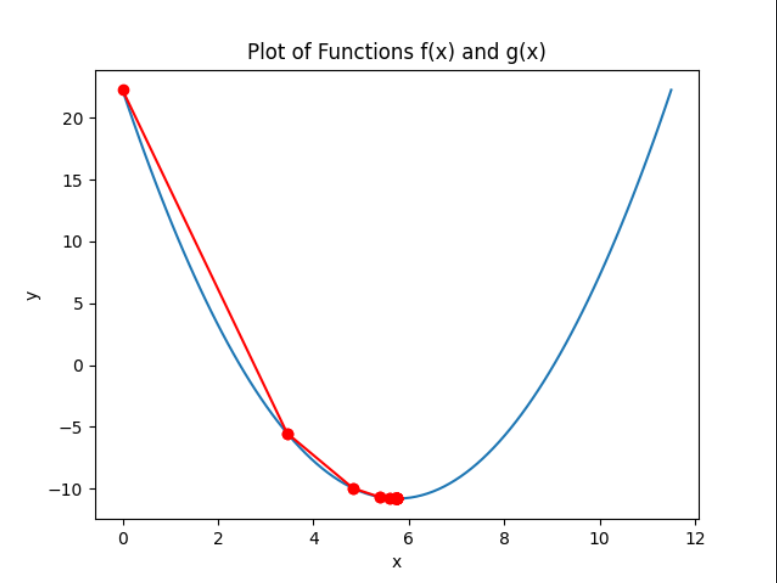
2. 学习率过小 (eta = 0.001， 更新次数较大)

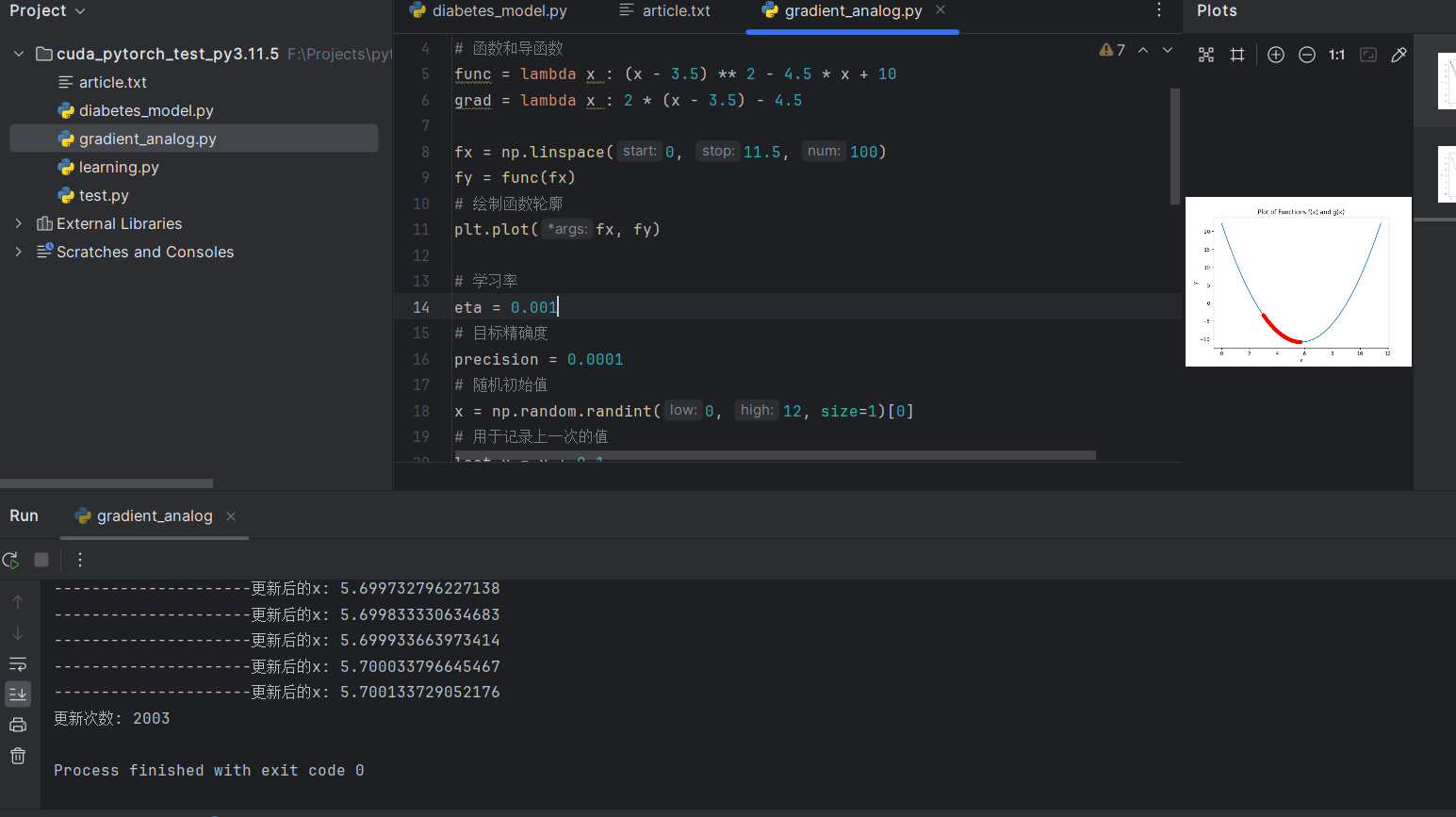
3. 学习率过大 (eta = 5， 无法解出答案)

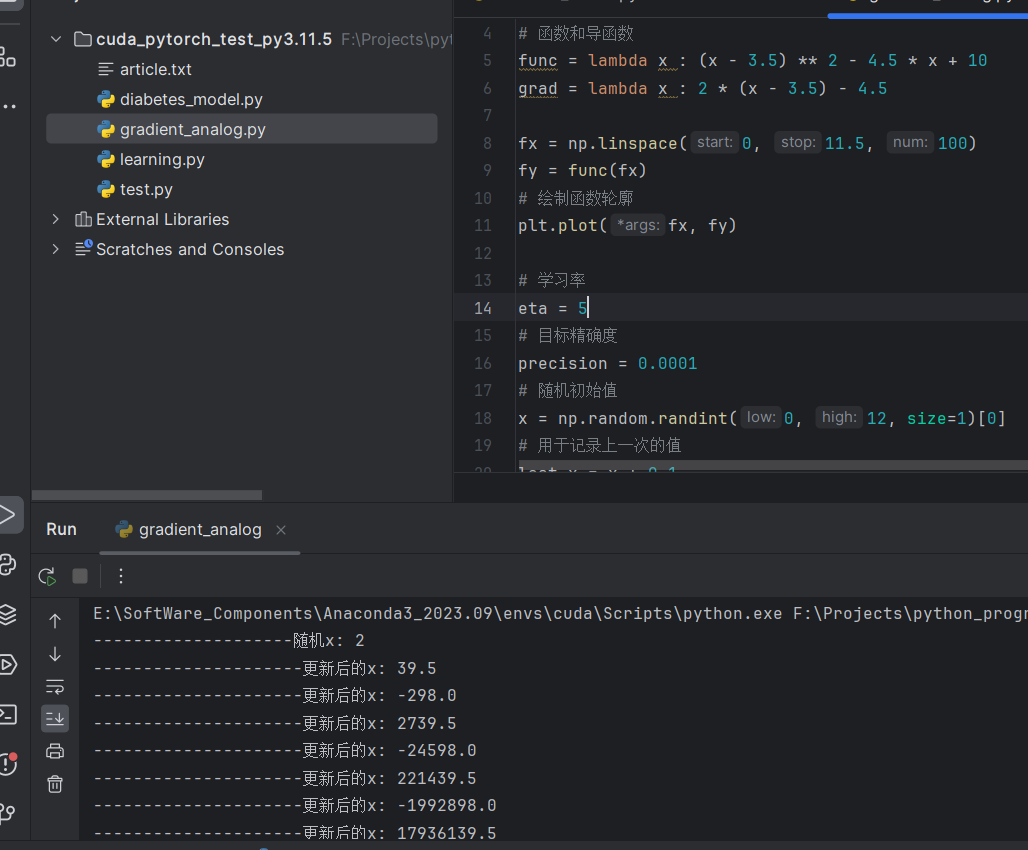
Full Code

import matplotlib.pyplot as plt
import numpy as np

# 函数和导函数
func = lambda x : (x - 3.5) ** 2 - 4.5 * x + 10
grad = lambda x : 2 * (x - 3.5) - 4.5

fx = np.linspace(0, 11.5, 100)
fy = func(fx)
# 绘制函数轮廓
plt.plot(fx, fy)

# 学习率
eta = 0.3
# 目标精确度
precision = 0.0001
# 随机初始值
x = np.random.randint(0, 12, size=1)[0]
print("--------------------随机x:", x)
# 用于记录上一次的值
last_x = x + 0.1

update_cnt = 0

# 多次while循环，每次梯度下降，更新，记录上一次的值
while True:
    # 循环出口:变化率过小
    if np.abs(x - last_x) < precision:
        break
    update_cnt += 1
    last_x = x
    x -= eta * grad(x)
    print("---------------------更新后的x:", x)

    # 绘制更新后的连线
    plt.plot([last_x, x], [func(last_x), func(x)], 'ro-')  # 'ro-' 表示红色

print("更新次数:", update_cnt)

# 添加标题和轴标签
plt.title('Plot of Functions f(x) and g(x)')
plt.xlabel('x')
plt.ylabel('y')
plt.show()