算法实验

一、分治法---寻找假币

1.实验内容

n(n>3)枚硬币中有一个假币（较轻），采用天平称重的方法找到假币。

提示：假设n枚硬币编号为0-n-1，使用数组保存所以硬币的重量，真币重量为2，假币重量为1，假币随机产生，使用二分法查找。

2.实验代码

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define max 1000

int a[max];
int n;
int WEIGHT(int low, int high )                //求所有硬币的总重量
{
    int weight = 0;
    for(int i = low; i <= high;i ++ )
        weight += a[i];
    return weight;
}
int SOLVE(int low, int high )                //进行假币判定
{
    if(low == high )                        //硬币堆只有一个硬币
    {
        return low;
    }
    if(low == high - 1 )                    //硬币堆只有两个硬币
    {
        if(a[low] < a[high] )
            return low;
        else
            return high;
    }
    int mid = (low + high ) / 2;
    int weight1, weight2;
    if((high - low + 1) % 2 == 0 )            //硬币个数为偶数
    {
        weight1 = WEIGHT(low, mid );
        weight2 = WEIGHT(mid + 1, high );
        printf("硬币%d-%d和硬币%d-%d之间比较一次：", low, mid, mid + 1, high );
    }
    else                                    //硬币个数为奇数
    {
        weight1 = WEIGHT(low, mid - 1 );
        weight2 = WEIGHT(mid + 1, high );
        printf("硬币%d-%d和硬币%d-%d之间比较一次：", low, mid - 1, mid + 1, high );
    }
    if(weight1 == weight2 )                    //假币是中间的那枚
    {
        printf("两堆硬币的重量相同\n" );
        return mid;
    }
    else if(weight1 < weight2 )                //假币在前半堆
    {
        printf("前半堆硬币重量轻\n");
        if((high - low + 1) % 2 == 0)        //前半堆的硬币个数为偶数
            return SOLVE(low, mid );
        else
            return SOLVE(low, mid - 1 );    //前半堆的硬币个数为奇数
    }
    else                                    //假币在后半堆
    {
        printf("后半堆硬币重量轻\n");
        return SOLVE(mid + 1, high );
    }
}
int main()
{
    printf("请输入硬币的个数（不超过1000个）：" );
    scanf("%d",&n );
    if(n <= 3)
    {
        printf("硬币个数至少为3个！\n" );
        system("pause");
    }
    else 
    {
        for(int i = 0; i < n; i ++ )
            a[i] = 2;
        srand((unsigned)time(NULL));
        int fake = rand() % n + 1;
        a[fake] = 1;
        printf("设置第%d个是假币\n", fake );
        printf("排查假币的过程\n" );
        printf("排查出的结果：第%d个是假币\n", SOLVE(0, n - 1 ) );
        system("pause");
        return 0;
    }
}

3.代码结果

 

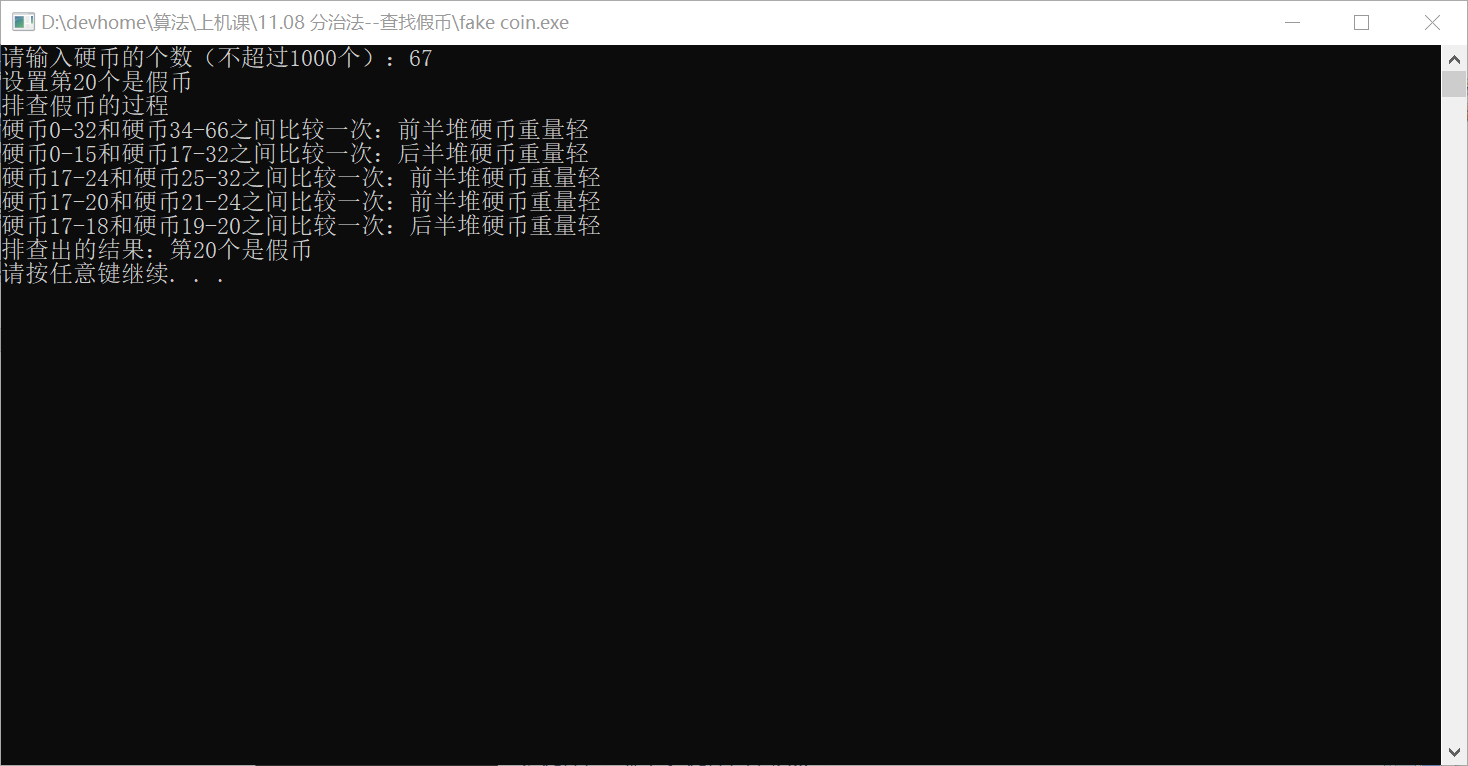
二、回溯法---求方程解

1.实验内容

编写一个试验程序，求出a,b,c,d,e满足a*b-c*d-e=1方程，其中所有变量的取值为1-5并且均不相同。

2.实验代码

#include<stdio.h>
#include<stdlib.h>
#define max 5
int n = max;
int a[max];                         //建立数组存储问题的解

void swap(int &x, int &y )           //交换两个元素
{
    int tmp = x;
    x = y;
    y = tmp;
}

void SOLVE(int a[] )                //输出方程的解
{
    printf("%d*%d-%d*%d-%d=1 所以%d,%d,%d,%d,%d是方程的一组解。\n",a[0],a[1],a[2],a[3],a[4],a[0],a[1],a[2],a[3],a[4]);
}
void dfs(int i )                   //进行深度优先遍历查询解 （以解空间为排列树）
{
    if(i == n)
    {
        if(a[0] * a[1] - a[2] * a[3] - a[4] == 1 )
            SOLVE(a);
    }
    else
    {
        for(int j = i; j < n; j ++ )
        {
            swap(a[i],a[j] );
            dfs(i+1 );
            swap(a[i],a[j] );
        }
    }
}

int main()
{
    for(int j = 0; j < n; j ++ )
        a[j] = j + 1;
    printf("求解方程的结果：\n" );
    dfs(0);
    system("pause" );
    return 0;
}

3.代码结果

 

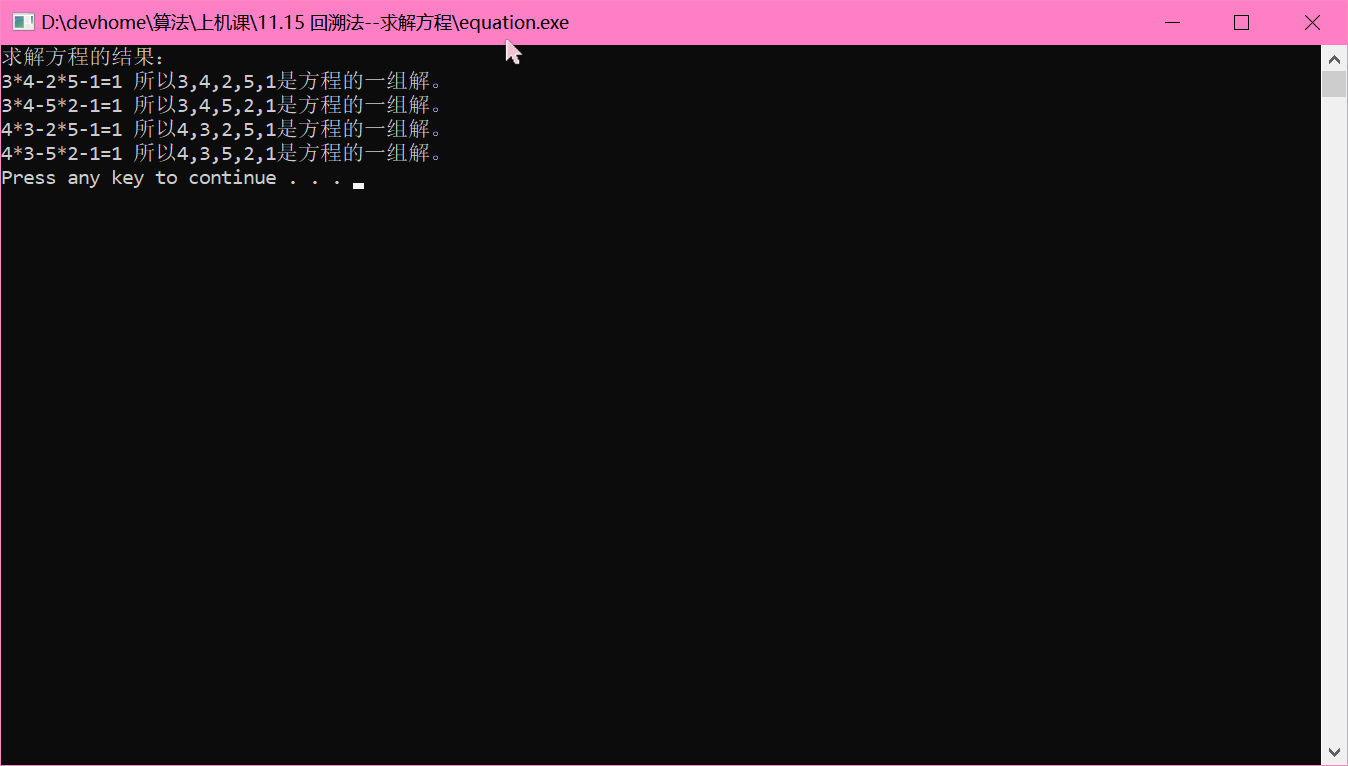
三、分支限界法---4皇后问题

1.实验内容

使用优先队列的分支界限法的方式对4皇后问题进行求解

2.实验代码

#include<stdio.h>
#include<stdlib.h>
#include<vector>
#include<queue>
using namespace std;
int n = 4;                         //皇后数量为4
int Count = 1;                     //结点个数

struct nodeType
{
    int no;                        //结点编号
    int row;                    //查找的行数
    vector<int>columns;            //已存在皇后的列
    bool operator < (const nodeType &a)const
    { return row < a.row;}
};

void output(nodeType e )        //输出结点位置
{
    if(e.row != -1 )
        printf("结点编号为%d，所在位置为(%d,%d)。\n",e.no, e.row, e.columns[e.row]);
    else
        printf("结点编号为%d，所在位置为(%d,？)。\n",e.no, e.row );
};
bool Check(vector<int>columns, int x, int y )    //判断位置(x,y)是否为皇后位置(x为当前行，y为当前列)
{
    int i = 0;
    while(i < x)                                    //检查x之前的行的情况
    {
        if((columns[i] == y )||(abs(columns[i] - y) == abs(i - x) ) ) //之前行的y已有皇后 或有皇后与当前位置成对角线
            return false;
        i ++;
    }
    return true;
};

void SOLVE()
{
    int x;
    int y;
    nodeType e,e1;
    priority_queue<nodeType> qu;
    e.no = Count ++; 
    e.row = -1;
    qu.push (e);
    printf("遍历：" );
    output(e );
    while(!qu.empty() )
    {
        e = qu.top();
        qu.pop();
        printf("出队：");
        output(e );
        if(e1.row == n - 1 )
        {
            printf("得到一个确定的皇后位置:\n" );
            for (x = 0; x < n; x ++ )
                printf("[%d,%d]为所得的位置。\n",x+1,e.columns[x]+1 );
                printf("\n");
            return;
        }
        else
        {
            for(y =0; y < n; y ++ )
            {
                x = e.row + 1;
                if(Check(e.columns, x, y ) )
                {
                    e1.no = Count ++;
                    e1.row = x;
                    e1.columns = e.columns;
                    e1.columns.push_back(y );
                    qu.push(e1 );
                    printf("进队的子结点:" );
                    output(e1 );
                }
            }
        }
    }

}

int main()
{
    printf("问题求解过程：\n");
    SOLVE();
    system("pause");
    return 0;
}

3.代码结果

 

 四、贪心法---饼干分配问题

1.实验内容

有一群孩子和一堆饼干，每个孩子有一个饥饿度，每个饼干都有一个大小。每个孩子只能吃
一个饼干，且只有饼干的大小不小于孩子的饥饿度时，这个孩子才能吃饱。求解最多有多少孩子
可以吃饱。

2.实验代码

#include<stdio.h>
#include<algorithm>
#include<stdlib.h>
using namespace std;
#define MAXN 5
#define maxn 10
int c[] = {6,5,100,53,11};
int b[] = {1,54,10,13,2,2,3,2,1,14,5};
int n=0;
int x[MAXN];
void solve()
{

    sort(c,c+MAXN);
    sort(b,b+maxn);
    for(int i = 0; i < MAXN; i++ )
    {
        for(int j = 0; j < maxn; j++ )
        {
            if(c[i]<=b[j])
            {
                n ++;
                i ++;
            }
        }
    }
}

int main()
{
    solve();
    printf("孩子的饥饿度为：");
    for(int i = 0; i < MAXN; i++ )
    {
        printf("%d ",c[i]);
    }
    printf("\n");
    printf("饼干的大小为：");
    for(int j = 0; j < maxn; j++ )
    {
        printf("%d ",b[j]);
    }
    printf("\n");
    printf("最多有%d个孩子可以吃饱\n",n);
    system("pause");
    return 0;
}

3.代码结果

 

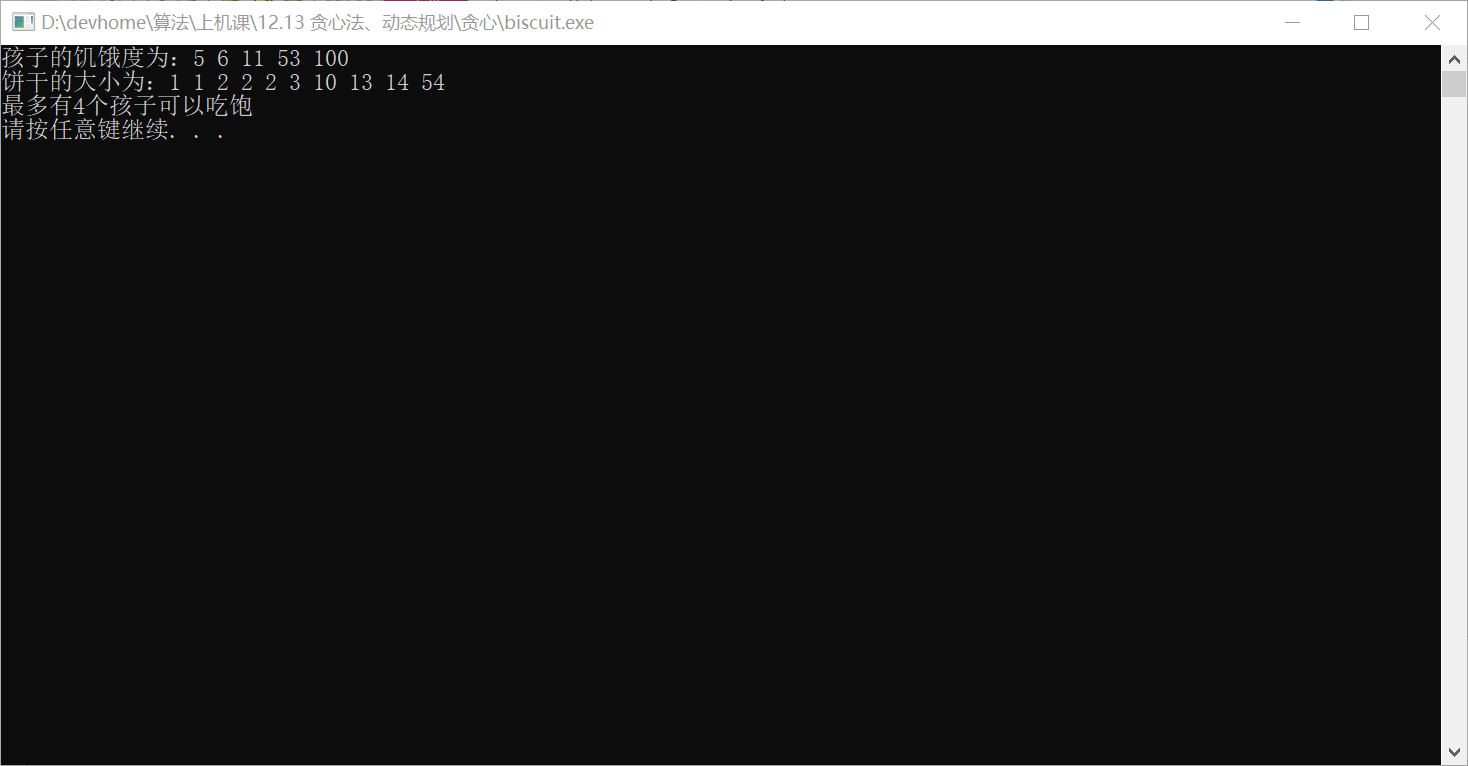
五、动态规划---整数拆分求最大乘积

1.实验内容

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 求出你可以获得的最大乘积。

2.实验代码

#include<stdio.h>
#include<vector>
#include<algorithm>
#include<stdlib.h>
using namespace std;
int main(int n, char **agrv)
{
    printf("请输入要求解的数字:");
    scanf("%d",&n );
    vector<int> dp(n+1 );
    dp[2] = 1;
    for(int i=3;i<=n;i++ )
　　{
　　　　for(int j = 1; j <= i-2;j ++ )
　　　　{
       　　dp[i] = max(dp[i], max(dp[i-j]*j,(i-j )*j ) );
       }
    }
    printf("最大乘积为：%d\n",dp[n] );
    system("pause" );
    return 0;
}

3.代码结果