Neural Networks and Deep Learning-Week2:Neural Networks Basics
一、Logistic Regression as a Neural Network
1. Binary Classification:二分分类法
举例识别图片中是否有猫(n_x = 64*64*3),最后得到特征向量矩阵,维度是12288


将图片转换为矩阵,其中:
- X中m代表的是第几个样本,i表示的是每个样本的第几个特征值。也就是每一列表示每个样本的样本特征值,一共多少列就有多少个样本,
- Y标签值代表第m个样本标签的值(0或1)

2. Logistic Regression:Logistic回归
- 概率型非线性回归模型,σ函数规范到0-1范围内
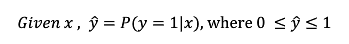

3. Logistic Regression Cost Function:回归损失函数
为了训练Logistic 回归模型的参数w和b,定义损失函数(误差函数)和成本函数来衡量w,b的准确性
值得注意的是:
- 损失函数L是单个训练样本中定义的,衡量了单个训练样本上的表现
- 成本函数J衡量了全体训练样本上的表现
具体说明如下:
- 损失函数(预测值与真实值之间的误差,比如于均方根差,但是均方根差在学习过程中会使求解问题变得不是凸优化问题,最终的梯度下降法得不到全局最优解,会得到多个局部最优解),
- 单个样本的回归损失函数以及样本总体的成本函数,目的都是达到最小
- 误差的平方

- 实际用到的损失函数:
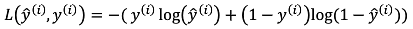
- 可行性分析:目的都是为了L函数最小,


4. Gradient Descent:梯度下降法
梯度下降法寻找w和b使得成本函数最小,成本函数是凸函数,因此可以找到最优解,梯度下降法的寻找最小值的基本原理

具体过程如下:从初始化参数开始,沿着最快下降的方向往下走,学习率α控制梯度下降法中的步长,通过偏导对每个偏量进行迭代更新
repeat{

}

- 初始化参数w,b
- 对每个偏量进行求导:dw,db
- 更新偏量进行迭代:w-αdw,b-αdb
- 朝着全局最小值得方向进行移动:w=w-αdw,b=b-αdb
- 直至得到全局最优解:w,b
5. Derivatives:导数
导数:也就是微积分中的导数公式没什么好说的

6. More Derivative Examples
更多导数的例子,同上
7. Computation graph:计算图
计算流程图,正向传播计算J=3*(a+bc)

8. Derivatives with a Computation Graph:计算图的导数计算
微积分中的链式法则,函数的反向求导

9. Logistic Regression Gradient Descent:Logistic回归中的梯度下降法
概率型非线性回归模型的单个样本的求导过程
- 基本公式


- 计算过程如下

10. Gradient Descent on m Examples:每个样本的梯度下降
概率型非线性回归模型的m个样本的求导过程

二、Python and Vectorization
11. Vectorization:向量化
向量化numpy.function 能够充分利用并行化,比使用for循环计算时间上快了300多倍,避免显示的使用for循环
#!/usr/bin/python2.7
# -*- coding: utf-8 -*-
import numpy as np
import time
# 使用numpy函数创建数组
a = np.array([1, 2, 3, 4])
print a
# 使用numpy函数创建矩阵
a = np.random.rand(1000000)
b = np.random.randn(1000000)
# 使用向量的方式计算两个矩阵的点乘积
tic = time.time()
c = np.dot(a, b)
toc = time.time()
print 'Vectorized version: ' + str(1000 * (toc - tic)) + 'ms'
# 使用for循环的方式计算两个矩阵的点乘积
c = 0
tic = time.time()
for i in range(1000000):
c += a[i] * b[i]
toc = time.time()
# print c
print 'for loop: ' + str(1000 * (toc - tic)) + 'ms'
12. More Vectorization Examples:更多向量化的例子
原则上避免显示的使用for循环,或者使用内置函数和新的算法代替显示的for循环,numpy中的向量操作函数
- 矩阵的乘积
# 矩阵的乘积
A = [[1, 2, 3],
[1, 2, 3],
[1, 2, 3]]
B = [[1, 2, 3],
[1, 2, 3],
[1, 2, 3]]
print np.dot(A, B)
U = np.zeros((3, 3))
for i in range(3):
for j in range(3):
for k in range(3):
U[i][j] += A[i][k] * B[k][j]
print U
-
矩阵函数
v = [[0, 0, 0],
[1, 1, 1],
[2, 2, 2]]
u = np.zeros((3, 3))
for i in range(3):
for j in range(len(v[i])):
u[i][j] = math.exp(v[i][j])
print u
u = np.exp(v)
print u
13. Vectorizing Logistic Regression:向量化Logistic 回归-正向传播
利用向量化,不使用任何显式的for循环进行多个样本预测值的计算
14. Vectorizing Logistic Regression's Gradient Output:向量化Logistic 回归反向传播-梯度计算
最终推导出不使用任何的显式的for循环进行一次梯度下降的迭代,如果需要迭代1000次那么在外层添加1000次的for循环即可

15. Broadcasting in Python:Python中的广播
Python中的广播例子Numpy
# 数组内部的聚合
A = np.array(
[[1.0, 2, 3],
[1.0, 2, 3],
[1.0, 2, 3]])
print np.sum(A, axis=1) # 1表示横向加,0表示纵向加
print A.sum(axis=1)
print 100 * A / A.sum(axis=1).reshape(1, 3)
# 全复制
A = np.array(
[[1, 2],
[2, 3],
[3, 4],
[4, 5]])
print A + 1
# 向下复制
A = np.array(
[[1, 2, 3],
[4, 5, 6]])
B = [100, 200, 300]
print A + B
# 向右复制
A = np.array(
[[1, 2, 3],
[4, 5, 6]])
B = [[100],
[200]]
print A + B
16. A note on python/numpy vectors:python中numpy向量的说明
注意在神经网络编程中注意使用矩阵的形式而不是数组的形式,不用秩为1的数组。要用矩阵的形式
np.array(),np.random.randn(5,1) a.reshape(5,1) assert(a.shape = (5,1))
17. Quick tour of Jupyter/iPython Notebooks
在线Python编程脚本的使用说明
18. Explanation of logistic regression cost function (optional)
损失函数和成本函数的推导说明
http://www.cnblogs.com/makexu/


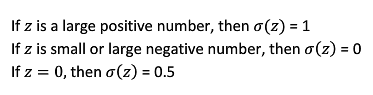

 浙公网安备 33010602011771号
浙公网安备 33010602011771号