决策树算法（ID3）

决策树：

　　决策树又称为判定树，是运用于分类的一种树结构，其中的每个内部节点代表对某一属性的一次测试，每条边代表一个测试结果，叶节点代表某个类或类的分布。
决策树的决策过程需要从决策树的根节点开始，待测数据与决策树中的特征节点进行比较，并按照比较结果选择选择下一比较分支，直到叶子节点作为最终的决策结果。

ID3：

　　ID3算法是由Ross Quinlan提出的决策树的一种算法实现，以信息论为基础，以信息熵和信息增益为衡量标准，从而实现对数据的归纳分类。

信息熵（entropy）：

　　熵描述了数据的混乱程度，熵越大，混乱程度越高，也就是纯度越低；反之，熵越小，混乱程度越低，纯度越高。 熵的计算公式如下所示：

　　　　　　　　　　　　　　　　　

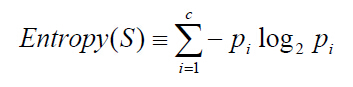
　　其中，S为所有事件集合，pi表示某一类i占总体数据数量的比例（可以理解为某一类发生的概率），c为总的类别数。以二分类问题为例，如果两类的数量相同，此时分类节点的纯度最低，熵等于1；如果节点的数据属于同一类时，此时节点的纯度最高，熵等于0

信息增益（information gain）：

　　是指信息划分前后的熵的变化，也就是说由于使用某个属性分割样例而导致的期望熵降低。也就是说，信息增益就是原有信息熵与属性划分后信息熵（需要对划分后的信息熵取期望值）的差值，具体公式表示为：

　　　　　　　　　　　　　　　　　　

　　其中A表示所有特征， Sv表示通过特征v划分出来的数据，|S|表示数据的长度信息，Gain表示节点的复杂度，Gain越高，说明复杂度越高。信息增益说白了就是分裂前的数据复杂度减去孩子节点的数据复杂度的和，信息增益越大，分裂后的复杂度减小得越多，分类的效果越明显。

构建一个决策树的过程：

　　1. 计算数据集S的信息熵.

　　2. 通过遍历所有特征A得到特征v，计算由特征v划分出来的分类信息Sv，然后计算Sv的信息熵

　　3. 计算通过A划分出来数据Sv的信息增益

　　4. 遍历所有的特征数据A，得到信息增益值最大的特征v，把v设为当前节点

　　5. 更新数据集合S和属性集合A（删除掉上一步中使用的属性，并按照属性值来划分不同分支的数据集合）

 　　6. 然后在次重复上面的1 - 6的步骤，直到所有属性都遍历完毕

 　　7. 完成所有决策树的构建

注意：该算法使用了贪婪搜索，从不回溯重新考虑之前的选择情况。

 coding：https://github.com/httpswlt/MLALGImplement/blob/master/Decision_Tree/ID3/dTreeID3.py