（笔记）斯坦福机器学习第九讲--经验风险最小化
本讲内容
1. Bias/Variance trade-off （偏差-方差权衡）
2. Empirical risk minimization(ERM) （经验风险最小化）
3. Union Bound/ Hoeffding inequality （联合界/霍夫丁不等式）
4. Uniform convergence （一致收敛）
1. 偏差方差权衡
对于上图左的情况，我们称之为欠拟合(under-fitting)，或者说，我们认为算法的偏差很高。高偏差意味着一个事实：即使你有无穷多的训练数据，算法依然不能拟合出数据的内在结构（比如二次结构）
对于上图右的情况，我们称之为过拟合(over-fitting)，或者说，我们认为算法的方差很高。高方差意味着一个事实：算法拟合出了数据中的一些奇怪的规律，或者说一些怪异的属性。
2. 经验风险最小化 ERM
定义一个线性分类器
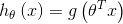
其中 
（note 
）
假设有m个训练样本，样本之间是独立同分布的。
定义训练误差：
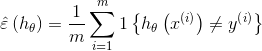
训练误差也被称为风险。
经验风险最小化： 选择分类器函数的参数，使得分类器的训练误差（training error）最小。
让我们换一种考虑方式：我们不是在选择最优分类器函数的参数，而是在选择最优的分类器函数。
定义假设类
假设类的每一个成员都是参数n+1个的线性分类器函数。
重新定义ERM：从假设类H中选取一个函数，使得分类器的训练误差最小。
实际上，我们并不关心训练误差的大小，我们关心的是分类器对于未知样本的预测能力，也就是一般误差（generation error）：
先引入两条引理：
1.联合界引理（Union Bound）：
令 
表示k个事件，这些事件不一定是独立的，
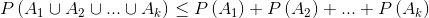
2.Hoeffding 不等式：
假设Z1,…,Zm为m个独立同分布（iid,independent and identically distributed）的随机变量,服从于伯努利分布，即
并且
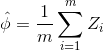
为这些随机变量的均值，给定 
，那么有
表达的是对真实分布的估计值与真实分布之间的差值大于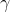 
的概率的上界，这个上界随着m的增加而指数下降。
考虑具有有限假设类的情形：
猜想类H具有k个假设
ERM会从H中选出具有最小训练误差的假设
需要证明
1. 训练误差是一个对一般误差的很好的近似
2. ERM选择的假设的一般误差存在上界
首先证明第一项，从猜想类H中任意选取一个假设 
,定义
服从伯努利分布，因此
其均值是假设的一般误差。
训练误差为
由Hoeffding不等式可知
假设m很大，即训练样本很多，那么训练误差将会以很大概率近似于一般误差。
定义事件 
为 
发生
有
那么对于整个猜想类来说
= 
两边同时用1减去
也就是说，在不小于 
的概率下，对于猜想类H中的所有假设h，其训练误差和一般误差之间的差距将会在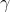 
以内。
这被称为 一致收敛。
定义
那么给定 
和 
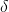解出
意思是，只要你的训练集合包含至少上述m这么多的样本，那么概率至少在 
下，有 
对H中的所有假设成立。
样本复杂度：为了达到一个特定的错误的界，你需要多大的训练集合。
误差界：
同样的，我们可以固定m和，得到
定义
为H中具有最小一般误差的假设，
为H中具有最小训练误差的假设，那么至少在 
的概率下，有
也就是说，我们选择的（具有最小训练误差的）假设的一般误差，和具有最小一般误差的假设的一般误差之间的差值存在 
的上界。
直观上，我们可以把第一项 
看成是选择假设的偏差，第二项 
看成选择假设的方差。
当我们将H替换为更复杂的猜想类H'，即H是H'的子集时，第一项只会变的更小，即偏差变小；而由于k的增大，第二项会变的更大，即方差变大。
将一切总结为两个定理如下：
第九讲完。
