ACM-ICPC 2018 沈阳赛区网络预赛
B. Call of Accepted
题意:计算算式,有\(d, +, -, *\)四种运算符和括号。\(d\)的级别最高,且是右结合,也就是\(xdydz = xd(ydz)\)。\(xdy\)表示每次在\([1, y]\)里取一个值,取\(x\)次,求最小值和最大值。
用递归计算算式,注意细节就行。
点击查看代码
#include <bits/stdc++.h>
using i64 = long long;
const i64 inf = 1e18;
struct Node {
i64 min, max;
};
Node operator + (const Node & a, const Node & b) {
return {a.min + b.min, a.max + b.max};
}
Node operator - (const Node & a, const Node & b) {
return {a.min - b.max, a.max - b.min};
}
Node operator * (const Node & a, const Node & b) {
i64 min = std::min({a.min * b.min, a.min * b.max, a.max * b.min, a.max * b.max});
i64 max = std::max({a.min * b.min, a.min * b.max, a.max * b.min, a.max * b.max});
return {min, max};
}
Node operator ^ (const Node & a, const Node & b) {
return {a.min, a.max * b.max};
}
std::string s;
std::map<char, int> rk;
Node dfs(int l, int r) {
if (l > r) {
return {0, 0};
}
int p = -1;
for (int i = l, cnt = 0; i <= r; ++ i) {
if (s[i] == '(') {
++ cnt;
} else if (s[i] == ')') {
-- cnt;
} else if (cnt == 0 && !isdigit(s[i])) {
if (p == -1 || rk[s[i]] >= rk[s[p]]) {
p = i;
}
}
}
if (p == -1) {
if (s[l] == '(') {
return dfs(l + 1, r - 1);
}
int res = std::stoi(s.substr(l, r - l + 1));
return {res, res};
}
auto L = dfs(l, p - 1);
auto R = dfs(p + 1, r);
if (s[p] == '+') {
return L + R;
} else if (s[p] == '-') {
return L - R;
} else if (s[p] == '*') {
return L * R;
} else {
return L ^ R;
}
}
void solve() {
auto ans = dfs(0, (int)s.size() - 1);
std::cout << ans.min << " " << ans.max << "\n";
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int t = 1;
rk['d'] = 1;
rk['*'] = 2;
rk['+'] = 3;
rk['-'] = 3;
while (std::cin >> s) {
solve();
}
return 0;
}
D. Made In Heaven
\(k\)短路板子。
点击查看代码
#include <bits/stdc++.h>
using i64 = long long;
int n, m;
void solve() {
int s, t, k, T;
std::cin >> s >> t >> k >> T;
-- s, -- t;
std::vector<std::vector<std::pair<int, i64>>> adj(n);
std::vector<std::vector<std::pair<int, i64>>> radj(n);
for (int i = 0; i < m; ++ i) {
int u, v;
i64 w;
std::cin >> u >> v >> w;
-- u, -- v;
adj[u].emplace_back(v, w);
radj[v].emplace_back(u, w);
}
const i64 inf = 1e18;
auto dijkstra = [&](int s) -> std::vector<i64> {
std::vector<i64> dist(n, inf);
using A = std::pair<i64, int>;
std::priority_queue<A, std::vector<A>, std::greater<A>> heap;
dist[s] = 0;
heap.emplace(0, s);
while (heap.size()) {
auto [d, u] = heap.top(); heap.pop();
if (d != dist[u]) {
continue;
}
for (auto & [v, w] : radj[u]) {
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
heap.emplace(dist[v], v);
}
}
}
return dist;
};
auto f = dijkstra(t);
auto a_star = [&](int s, int t) -> i64 {
if (f[s] > T) {
return inf;
}
using A = std::tuple<i64, i64, int>;
std::priority_queue<A, std::vector<A>, std::greater<A>> heap;
heap.emplace(f[s], 0, s);
int cur = 0;
while (heap.size()) {
auto [_, d, u] = heap.top(); heap.pop();
if (u == t) {
++ cur;
}
if (cur == k) {
return d;
}
if (d > T) {
return inf;
}
for (auto & [v, w] : adj[u]) {
heap.emplace(d + w + f[v], d + w, v);
}
}
return inf;
};
if (a_star(s, t) <= T) {
std::cout << "yareyaredawa\n";
} else {
std::cout << "Whitesnake!\n";
}
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int t = 1;
while (std::cin >> n >> m) {
solve();
}
return 0;
}
F. Fantastic Graph
题意:给你一个二分图和一些边,你需要选择一些边,使得每个点的度数都在\([L, R]\)里。
把原图边视为上界为\(1\)下界为\(0\)的边,然后建立源点和汇点,源点向左部点连上界为\(R\)下界为\(L\)的边,右部点向汇点连上界为\(R\)下界为\(L\)的边。这样就变成了有源汇的上下界可行流问题。
点击查看代码
#include <bits/stdc++.h>
using i64 = long long;
const int N = 4010, M = (6000 + 4000 * 2 + 5) * 2 + 10, inf = 1e8;
int head[N], ver[M], next[M], low[M], cap[M], tot;
int d[N], cur[N], A[N];
int n, m, k, S, T;
void add(int x, int y, int l, int u) {
A[x] -= l;
A[y] += l;
ver[tot] = y; cap[tot] = u - l; low[tot] = l; next[tot] = head[x]; head[x] = tot ++ ;
ver[tot] = x; cap[tot] = 0; next[tot] = head[y]; head[y] = tot ++ ;
}
bool bfs() {
std::queue<int> q;
memset(d, -1, sizeof d);
q.push(S);
d[S] = 0; cur[S] = head[S];
while (q.size()) {
int u = q.front(); q.pop();
for (int i = head[u]; i != -1; i = next[i]) {
int v = ver[i];
if (d[v] == -1 && cap[i]) {
d[v] = d[u] + 1;
cur[v] = head[v];
if (v == T) {
return true;
}
q.push(v);
}
}
}
return false;
}
int find(int u, int limit) {
if (u == T) {
return limit;
}
int flow = 0;
for (int i = cur[u]; i != -1 && flow < limit; i = next[i]) {
int v = ver[i];
cur[u] = i;
if (d[v] == d[u] + 1 && cap[i]) {
int t = find(v, std::min(cap[i], limit - flow));
if (t == 0) {
d[v] = -1;
} else {
cap[i] -= t; cap[i ^ 1] += t;
flow += t;
}
}
}
return flow;
}
int dinic() {
int r = 0, flow;
while (bfs()) {
while (flow = find(S, inf)) {
r += flow;
}
}
return r;
}
void solve() {
int L, R;
std::cin >> L >> R;
memset(head, -1, sizeof head);
tot = 0;
memset(A, 0, sizeof A);
S = n + m + 3, T = n + m + 4;
int s = n + m + 1, t = n + m + 2;
for (int i = 0; i < k; ++ i) {
int u, v;
std::cin >> u >> v;
add(u, v + n, 0, 1);
}
for (int i = 1; i <= n; ++ i) {
add(s, i, L, R);
}
for (int i = n + 1; i <= n + m; ++ i) {
add(i, t, L, R);
}
add(t, s, 0, inf);
int sum = 0;
for (int i = 1; i <= n + m + 2; ++ i) {
if (A[i] > 0) {
sum += A[i];
add(S, i, 0, A[i]);
} else if (A[i] < 0) {
add(i, T, 0, -A[i]);
}
}
if (dinic() != sum) {
std::cout << "No\n";
} else {
std::cout << "Yes\n";
}
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int t = 1;
while (std::cin >> n >> m >> k) {
if (n == 0) {
break;
}
std::cout << "Case " << t ++ << ": ";
solve();
}
return 0;
}
G. Spare Tire
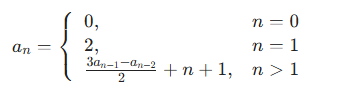
题意:给你\(n, m\),对于\([1, n]\)里每个和\(m\)互质的\(i\),求\(a_i\)的和。
首先打表发现\(a_i = i^2 + i\)。
那么我们可以用容斥的思想,先把所有数的和算上:\(\sum_{i=1}^{n} i^2+i\),\(i^2\)和\(i\)的和都可以直接算。
然后我们给\(m\)分解质因子,枚举质因子的所有组合,假设现在乘积为\(x\),那么这个组合包含的所有数就是\(\sum_{k=1}^{\lfloor \frac{n}{x} \rfloor} (kx)^2 + kx\)。根据质因子个数的奇偶判断是加上还是减去就行。这个式子也容易计算。
点击查看代码
#include <bits/stdc++.h>
using i64 = long long;
const int mod = 1e9 + 7;
int n, m;
std::vector<int> primes, minp;
void init(int n) {
primes.clear();
minp.assign(n + 1, 0);
for (int i = 2; i <= n; ++ i) {
if (minp[i] == 0) {
primes.push_back(i);
minp[i] = i;
}
for (auto & p : primes) {
if (p * i > n) {
break;
}
minp[p * i] = p;
if (minp[i] == p) {
break;
}
}
}
}
int power(int a, int b) {
int res = 1;
for (;b;b >>= 1, a = 1LL * a * a % mod) {
if (b & 1) {
res = 1LL * res * a % mod;
}
}
return res;
}
const int inv2 = power(2, mod - 2), inv6 = power(6, mod - 2);
int get1(int n) {
return (i64)n * (n + 1) % mod * inv2 % mod;
}
int get2(int n) {
return (i64)n * (n + 1) % mod * (2 * n % mod + 1) % mod * inv6 % mod;
}
void solve() {
std::vector<int> a;
for (auto & p : primes) {
if (p * p > m) {
break;
}
if (m % p == 0) {
a.push_back(p);
while (m % p == 0) {
m /= p;
}
}
}
if (m > 1) {
a.push_back(m);
}
int ans = (get1(n) + get2(n)) % mod;
int tot = a.size();
for (int i = 1; i < 1 << tot; ++ i) {
int cnt = __builtin_popcount(i);
int cur = 1;
for (int j = 0; j < tot; ++ j) {
if (i >> j & 1) {
cur *= a[j];
}
}
if (cur > n) {
continue;
}
int k = n / cur;
int val = ((i64)get1(k) * cur % mod + (i64)get2(k) * cur % mod * cur % mod) % mod;
if (cnt & 1) {
ans = (ans - val + mod) % mod;
} else {
ans = (ans + val) % mod;
}
}
std::cout << ans << "\n";
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int t = 1;
init(10000);
while (std::cin >> n >> m) {
if (n == 0) {
break;
}
solve();
}
return 0;
}
I. Lattice&s basics in digital electronics
模拟
点击查看代码
#include <bits/stdc++.h>
using i64 = long long;
void solve() {
int n, k;
std::cin >> n >> k;
std::map<std::string, int> mp;
for (int i = 0; i < k; ++ i) {
std::string s;
int x;
std::cin >> x >> s;
mp[s] = x;
}
auto get = [&](char c) -> std::string {
int n = c - '0';
if (c >= 'A' && c <= 'Z') {
n = 10 + c - 'A';
}
std::string res;
for (int i = 3; i >= 0; -- i) {
res += (n >> i & 1) ? '1' : '0';
}
return res;
};
std::string s;
std::cin >> s;
std::string t;
for (auto & c : s) {
if (c >= 'a' && c <= 'z') {
c -= 32;
}
t += get(c);
}
s.clear();
for (int i = 0; i + 8 < t.size(); i += 9) {
int cnt = 0;
for (int j = i; j < i + 9; ++ j) {
cnt += t[j] == '1';
}
if (cnt & 1) {
s += t.substr(i, 8);
}
}
std::string ans;
t.clear();
for (auto & c : s) {
t += c;
if (mp.count(t)) {
ans += (char)mp[t];
t.clear();
}
if (ans.size() > n) {
break;
}
}
std::cout << ans.substr(0, n) << "\n";
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int t = 1;
std::cin >> t;
while (t -- ) {
solve();
}
return 0;
}
J. Ka Chang
题意:给你一棵以一为根的树,两种操作,一种是给深度为\(l\)的点都加上\(x\),一种是查询\(u\)的子数和。
根号分治。
对于第一个操作,如果深度为\(l\)的点小于等于\(\sqrt{n}\)个,直接暴力加就行,可以用树状数组维护\(dfs\)序。否则用个数组存一下深度为\(l\)的点都加了多少。
对于第二个操作,先计算\(dfs\)序子树区间的和。然后我们可以预处理用\(map\)存每个点有多少个深度大于\(\sqrt{n}\)的点,因为这样的深度个数不超过\(\frac{n}{\sqrt{n}}\)个,不会爆炸。然后枚举所有这些深度,看有多少点在这个深度累加答案就行了。
点击查看代码
#include <bits/stdc++.h>
using i64 = long long;
struct Fenwick {
std::vector<i64> tr;
int n;
Fenwick(){};
Fenwick(int _n) {
n = _n;
tr.assign(_n + 1, 0);
}
void add(int x, int v) {
for (int i = x; i <= n; i += i & -i) {
tr[i] += v;
}
}
i64 query(int x) {
i64 res = 0;
for (int i = x; i > 0; i -= i & -i) {
res += tr[i];
}
return res;
}
i64 sum(int l, int r) {
return query(r) - query(l - 1);
}
};
void solve() {
int n, q;
std::cin >> n >> q;
std::vector<std::vector<int>> adj(n);
for (int i = 1; i < n; ++ i) {
int u, v;
std::cin >> u >> v;
-- u, -- v;
adj[u].push_back(v);
}
std::vector<int> in(n), out(n), d(n);
std::vector<std::vector<int>> a(n);
int idx = 0;
auto dfs = [&](auto & self, int u) -> void {
in[u] = idx ++ ;
a[d[u]].push_back(u);
for (auto & v : adj[u]) {
d[v] = d[u] + 1;
self(self, v);
}
out[u] = idx - 1;
};
dfs(dfs, 0);
int T = std::sqrt(n);
std::vector<std::map<int, int>> mp(n);
auto dfs1 = [&](auto & self, int u) -> void {
for (auto & v : adj[u]) {
self(self, v);
for (auto & [x, y] : mp[v]) {
mp[u][x] += y;
}
}
if (a[d[u]].size() >= T) {
mp[u][d[u]] += 1;
}
};
dfs1(dfs1, 0);
std::vector<i64> sum(n);
Fenwick tr(2 * n);
while (q -- ) {
int op;
std::cin >> op;
if (op == 1) {
int l, x;
std::cin >> l >> x;
if (a[l].size() <= T) {
for (auto & u : a[l]) {
tr.add(in[u] + 1, x);
}
} else {
sum[l] += x;
}
} else {
int u;
std::cin >> u;
-- u;
i64 ans = tr.sum(in[u] + 1, out[u] + 1);
for (auto & [x, y] : mp[u]) {
ans += sum[x] * y;
}
std::cout << ans << "\n";
}
}
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
solve();
return 0;
}
K. Supreme Number
题意:一个数的所以子序列都是质数这个数就是好的,求小于等于\(n\)的最大的好数。
显然\(1\)最多出现两次,因为\(111\)不是质数,其它数最多出现一次,因为\(xx\)是\(11\)的倍数。
那么合法的数在\(1000\)以内,暴力枚举出来就行。
点击查看代码
#include <bits/stdc++.h>
using i64 = long long;
std::vector<int> a;
bool is_primes(int n) {
for (int i = 2; i * i <= n; ++ i) {
if (n % i == 0) {
return false;
}
}
return true;
}
bool check(int n) {
std::string s = std::to_string(n);
auto dfs = [&](auto & self, int u, int x) -> bool {
if (u == s.size()) {
return is_primes(x);
}
if (!self(self, u + 1, x) || !self(self, u + 1, x * 10 + s[u] - '0')) {
return false;
}
return true;
};
return dfs(dfs, 0, 0);
}
void init() {
for (int i = 1; i <= 999; ++ i) {
if (check(i)) {
a.push_back(i);
}
}
}
void solve() {
std::string s;
std::cin >> s;
if (s.size() >= 4) {
std::cout << a.back() << "\n";
} else {
auto it = std::upper_bound(a.begin(), a.end(), std::stoi(s));
-- it;
std::cout << *it << "\n";
}
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int t = 1;
init();
std::cin >> t;
for (int i = 1; i <= t; ++ i) {
std::cout << "Case #" << i << ": ";
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号