网络流

最大流

1.最大流

定义

自行意会。

原理

找一条 \(S-T\) 的正权路径，给里面加流量。

显然是错的，但是可以再存反边，类似一种反悔的思想。其最大流量为 \(0\)。

此处的边权皆为空余流量。

实现

EK/FF

用 DFS、BFS 打暴力。

ISAP

预处理每个点到 \(T\) 的反图最短路（实际无必要），以此分层，DFS 分配新流量。

有一些显然的优化。GAP 断层优化、当前弧优化。还有层数较小时，可以玄学少跑几次。

namespace flow{
	const int N=1e5+10,M=2e5+10;
	int h[N],ne[M],e[M],w[M],idx=1,S,T,tot,cnt[N],dis[N],cur[N];
	inline void addE(int u,int v,int x){
		ne[++idx]=h[u],h[u]=idx,e[idx]=v,w[idx]=x;
	}
	inline void add(int u,int v,int x){
		addE(u,v,x),addE(v,u,0);
	}
	inline int dfs(int u,int sum){
		if(u==T) return sum;
		int ss=0;
		for(int &i=cur[i];i;i=ne[i]){
			int v=e[i];
			if(w[i]<=0||dis[u]!=dis[v]+1) continue;
			int tmp=dfs(v,min(w[i],sum-ss));
			ss+=tmp,w[i]-=tmp,w[i^1]+=tmp;
			if(sum==ss||dis[S]>=tot) return ss;
		}
		if(!--cnt[dis[u]]) dis[S]=tot;
		++cnt[++dis[u]];
		cur[u]=h[u];
		return ss;
	}
	inline int work(){
		int res=0;
		for(int i=1;i<=tot;++i) cur[i]=h[i];
		while(dis[S]<tot) res+=dfs(S,inf);
		return res;
	}
}
using flow::S;
using flow::T;
using flow::tot;
using flow::add;
using flow::work;

注意

• 链式前向星建图正反边一定要相邻建。

• idx 初值要是奇数。

• 网格图用 id[][] 数组时，一定要考虑是不是赋过值的。可以分成多个部分，不要太压行。

• 数组大小。

建模

• 神奇猜结论。

• 结合 DP 状态。

• 用点来分流。

• 图上分层拆点跑残量网络，直至流量大于等于某值（EK/dinic 更优）。

• 转最小割，跑 DP。

---

2.最小割

定义

分成包含 \(S\) 和 \(T\) 的两部分点，使 \(S\) 部到 \(T\) 部的边流量和最小。

原理

值等于最大流，考虑非最大流就会有未填满的路径。

实现

同最大流。

建模

• 核心，不能有通路。

• 网格图染色（2或4），建图。但不能一见网格图就一定是。

• 串联=或；并联=且。

• 点权转边权。

• 拆点、限流。

• 每个点分类型，有代价。

• 一组在一起有额外代价（建模同下）。

• 每个点分类型，有贡献。
• 一组在一起有额外贡献（建模如嫖来的图，\(C_i\) 在就意味着它所连的组必须没有连向 \(T\) 的）。

• 当在同一个集合有代价时，可以选择一类路径反向、交换集合边权。

• 找边数最小最小割，增量法（乘）。

---

最大权闭合子图

定义

没有向外出边的点集，使其点权和最大。

原理

\(\text{正权和}-\text{最小割}\)。正权点不要会有代价，负权点要也会有代价。

实现

在原图基础上，\(S\) 向正权点连边权，负权点向 \(T\) 连边权相反数。

建模

• 有明确带权依赖关系。

• 二分图两边相等，一边加 inf，一边减 inf；扩倍，压缩信息。

---

3.费用流

定义

最值费用最大流。

原理

贪心，优先增广最短路（ISAP 当中最短路带权）。

实现

SPFA 求最短路（有负环，只走有流量的边），最短路上增广。

• 多路增广。

可以类似 SAP，但是无优化。

细节

静态数组作队列，一定要判越界，循环使用内存。

memset 最后尽量用 sizeof，不要自己算，可以把点数开精确一点。（悲

可以动态加边。

建模

最大流满足一个限制，费用再求另一个最值。

拆点定流

还是拆点，但是不好限制每一个点刚刚好有给定的流量。考虑直接让拆出来的 \(2n\) 个点凭空获得流（当然，有代价），再通过题目条件，把流分出去，这里的“分”具有偏序关系，同一层的点也可以视情况有偏序关系。

另一道

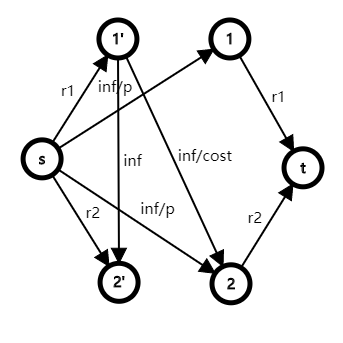
拆点定向

网格图，只有连成环的拐弯才有权值。染色，分类。一个点分上下方向和左右方向，连两条边，一条有权，一条无权，最终减去一倍权和。相邻对应连。

• 总的减去一部分。预先设置一些状态，再调整。

• 拆绝对值。

---

4.上下界网络流

定义

每个边的流量有上下界。

可行流

定义

问有没有解。

最大/小流

定义

在满足限制下的最值。

实现

namespace udflow{
	const int N=1e5+10,M=2e6+10;
	int S,T,S1,T1,S2,T2,tot,h[N],ne[M],e[M],w[M],idx=1,cur[N],cnt[N],dis[N],exfl,du[N];
	inline void addE(int u,int v,int x){
		ne[++idx]=h[u],h[u]=idx,e[idx]=v,w[idx]=x;
	}
	inline void add(int u,int v,int l,int r){
		du[v]+=l,du[u]-=l;
		addE(u,v,r-l),addE(v,u,0);
	}
	inline int dfs(int u,int sum){
		if(u==T2) return sum;
		int ss=0;
		for(int &i=cur[u];i;i=ne[i]){
			int v=e[i];
			if(w[i]<=0||dis[u]!=dis[v]+1) continue;
			int tmp=dfs(v,min(w[i],sum-ss));
			ss+=tmp,w[i]-=tmp,w[i^1]+=tmp;
			if(sum==ss||dis[S2]>=tot) return ss;
		}
		if(!--cnt[dis[u]]) dis[S2]=tot;
		++cnt[++dis[u]];
		cur[u]=h[u];
		return ss;
	}
	inline void init(){
		memset(dis,0,sizeof dis);
		memset(cnt,0,sizeof cnt);
	}
	inline int work(){
		addE(T,S,inf),addE(S,T,0);
		int bg=idx;
		for(int i=1;i<=tot;++i){
			if(du[i]>0) addE(S1,i,du[i]),addE(i,S1,0),exfl+=du[i];
			if(du[i]<0) addE(i,T1,-du[i]),addE(T1,i,0);
		}
		for(int i=1;i<=tot;++i) cur[i]=h[i];
		int res=0;
		S2=S1,T2=T1;
		while(dis[S2]<tot) res+=dfs(S2,inf);
		if(res!=exfl) return -1;
		init();
		for(int i=1;i<=tot;++i) cur[i]=h[i];
		S2=S,T2=T;
		res=w[bg];
		w[bg]=w[bg-1]=0;
		while(dis[S2]<tot) res+=dfs(S2,inf);
		return res;
	}
}
using udflow::S;
using udflow::T;
using udflow::S1;
using udflow::T1;
using udflow::tot;
using udflow::add;
using udflow::work;

费用流

定义

区分一下最值费用最大流和单纯的费用流。

后者在增广的 dis 不优后就可以退出了。

实现

namespace udflow{
	const int N=1e5+10,M=2e6+10;
	int S,T,S1,T1,S2,T2,tot,h[N],ne[M],e[M],w1[M],w2[M],idx=1,q[N],hh,tt,sum,flow[N],pre[N],dis[N],du[N];
	bool vis[N];
	inline void addE(int u,int v,int x1,int x2){
		ne[++idx]=h[u],h[u]=idx,e[idx]=v,w1[idx]=x1,w2[idx]=x2;
	}
	inline void add(int u,int v,int l,int r,int x){
		sum+=l*x;
		du[v]+=l,du[u]-=l;
		addE(u,v,r-l,x),addE(v,u,0,-x);
	}
	inline bool spfa(){
		memset(dis,0x3f,sizeof dis);
		memset(flow,0x3f,sizeof flow);
		memset(vis,0,sizeof vis);
		hh=0,tt=1;
		q[0]=S2;
		dis[S2]=0;
		while(hh!=tt){
			int u=q[hh++];
			if(hh==N) hh=0;
			vis[u]=0;
			for(int i=h[u];i;i=ne[i]){
				int v=e[i],tmp=dis[u]+w2[i];
				if(w1[i]>0&&dis[v]>tmp){
					dis[v]=tmp;
					flow[v]=min(flow[u],w1[i]);
					pre[v]=i^1;
					if(!vis[v]){
						vis[v]=1;
						q[tt++]=v;
						if(tt==N) tt=0;
					}
				}
			}
		}
		return dis[T]<inf;
	}
	inline int work(){
		addE(T,S,inf,0),addE(S,T,0,0);
		for(int i=1;i<=tot;++i){
			if(du[i]>0) addE(S1,i,du[i],0),addE(i,S1,0,0);
			if(du[i]<0) addE(i,T1,-du[i],0),addE(T1,i,0,0);
		}
		int res=sum;
		S2=S1,T2=T1;
		while(spfa()){
			res+=dis[T2]*flow[T2];
			for(int i=T2;i!=S2;i=e[pre[i]]){
				w1[pre[i]]+=flow[T2];
				w1[pre[i]^1]-=flow[T2];
			}
		}
		return res;
	}
}
using udflow::S;
using udflow::T;
using udflow::S1;
using udflow::T1;
using udflow::tot;
using udflow::add;
using udflow::addE;
using udflow::work;