A-口粮运输

题意

\(\color{pink}\text{自己看}\)

分析

令点权 \(w_i=a_i-b_i\)。

首先有一个会被套路的一个假做法：对于 \(a\ge b\) 的点，放左部；对于 \(a<b\) 的点，放右部，形成一个二分图。然后不同部的点对连一条边权为它们的最短路长度的边。然后试图去平衡粮食的数量。

一开始感觉很可做，但是经过 \(1\) 个小时，发现会有问题。先看一个 hack。

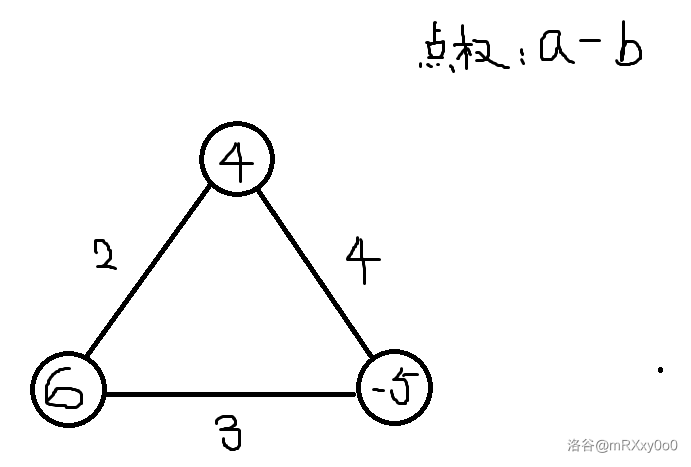
最优方法：\(4\) 先给 \(6\)，中途浪费 \(2\)，现在 \(6\) 变成 \(8\)；\(8\) 再给 \(-5\)，中途浪费 \(3\)，刚好全是 \(0\)。

然而从最短路走无法达成这一点。思考为什么，发现原因是走最短路的时候多浪费了一些，而最优方法浪费的要少一点。

考虑一条链，除链尾外其他点 \(w\ge0\)。发现从链头传递到链尾的最大值是 \(\sum w-\sum len\)（\(\text{点权和}-\text{边权和}\)），要求所有前缀 \(\ge0\)。

在只有一个点 \(w<0\) 的情况下，这是一棵树（可能一条链不够填满它）。这启示我们把整个方案分成很多棵树，对此，找最小生成树即可。

此时，重新思考原问题，直觉上来说是由很多棵最小生成树组成的（后来发现每边最多经过一次），考虑枚举生成树上的点集，在加上子集枚举分成两部分，记录该点集是否能成功填满即可。

单组数据复杂度 \(O(3^n+2^n\times m)\)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N=16,inf=1e9;
int n,m,a[N],b[N],fa[N];
bool f2[1<<N];
struct node{
	int u,v,w;
}len[N*N];
inline bool cmp(node x,node y){
	return x.w<y.w;
}
inline int gf(int x){
	return fa[x]==x?x:fa[x]=gf(fa[x]);
}
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;++i) scanf("%d%d%d",&len[i].u,&len[i].v,&len[i].w);
		sort(len+1,len+1+m,cmp);
		for(int i=1;i<=n;++i) scanf("%d%d",&a[i],&b[i]);
		bool fd=0;
		memset(f2,0,sizeof f2);
		for(int s=0;s<1<<n;++s){
			int ff=1,tot=0,s1=0;
//			cout<<s<<"---\n";
			for(int i=0;i<n;++i){
//				cout<<i<<" "<<a[i+1]<<" "<<b[i+1]<<"\n";
				if(s&(1<<i)) ++tot,s1+=a[i+1]-b[i+1];
				else if(a[i+1]<b[i+1]) ff=0;
				fa[i+1]=i+1;
			}
			int sum=0,cnt=0;
			for(int i=1;i<=m;++i){
				if((s&(1<<len[i].u-1))&&(s&(1<<len[i].v-1))){
					int x=gf(len[i].u),y=gf(len[i].v);
					if(x!=y){
						fa[x]=y;
						++cnt;
						sum+=len[i].w;
					}
				}
			}
			f2[s]=(s1>=sum&&cnt==tot-1);
//			cout<<s<<" "<<tot<<" "<<cnt<<" "<<s1<<" "<<sum<<"\n";
			for(int ss=s;ss;ss=(ss-1)&s){
				f2[s]|=(f2[ss]&&f2[s^ss]);
			}
			if(ff&&f2[s]){
				fd=1;
				break;
			}
		}
		puts(fd?"Yes":"No");
	}
	return 0;
}