P3209 [HNOI2010] 平面图判定

VERY GOOOOOOOOOOOD的好题！

一开始没有发现给已经给了回路想了好久怎么求

平面图的重要定理：\(m≤3n-6\)

考虑这些边可以在环内也可以在环外，但是如果满足\(x1<x2<y1<y2\)就一定不能在同侧，\(m^2\)判断一下有没有只能在同侧的边，利用带权并查集就可以解决。

但是我太懒了，不想写带权的，所以我们可以用一种奇技淫巧：

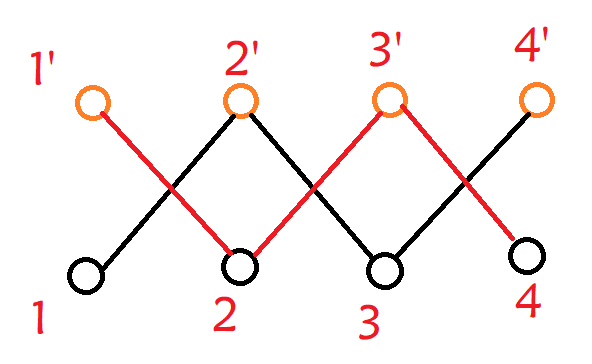
如图，只有偶数条边(1,3)才算在同一个并查集

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define orz cout<<"lyakioi!!!!!!!!!!!!!!!!!"<<endl
inline int r(){int s=0,k=1;char c=getchar();while(!isdigit(c)){if(c=='-')k=-1;c=getchar();}while(isdigit(c)){s=s*10+c-'0';c=getchar();}return s*k;}
int T,n,m,a[505][505],from[10001],to[10001],ring[10001],fa[10001],root1,root2,t[10001];
int father(int x)
{
	if(fa[x]!=x)fa[x]=father(fa[x]);
	return fa[x];
}
void unit(int x,int y)
{
	int fax=father(x);
	int fay=father(y);
	fa[fax]=fay;
}
int main()
{
	T=r();
	while(T--)
	{
		memset(a,0,sizeof(a));
		memset(t,0,sizeof(t)); 
		memset(fa,0,sizeof(fa));
		memset(ring,0,sizeof(ring));
		n=r();m=r();
		root1=root2=0;
		for(int i=1;i<=m;i++)
		{
			from[i]=r();
			to[i]=r();
//			fa[i]=i;
		}
		for(int i=1;i<=m*2;i++)
		fa[i]=i;
		for(int i=1;i<=n;i++)
		{
			ring[i]=r();
			t[ring[i]]=i;
			if(i>1)a[i][i-1]=a[i-1][i]=1;
		}
		a[1][n]=a[n][1]=1;
		if(m>n*3-6)
		{
			cout<<"NO"<<endl;
			continue;
		}
		int flag=0;
		for(int i=1;i<=m;i++)
		for(int j=i+1;j<=m;j++)
		{
			if(flag)break;
			int x1=from[i],y1=to[i];
			x1=t[x1];y1=t[y1];
			if(x1>y1)swap(x1,y1);
			int x2=from[j],y2=to[j];
			x2=t[x2];y2=t[y2];
			if(x2>y2)swap(x2,y2);
			if(a[x1][y1]||a[x2][y2])continue;
    		if( x1 == x2 || y1 == y2 || x1 == y2 || x2 == y1 )continue;
			if(x1<x2&&x2<y1&&y1<y2||x2<x1&&x1<y2&&y2<y1)
			{
				int fax=father(i);
				int fay=father(j);
//				cout<<i<<" 和 "<<j<<"不能在一起"<<endl;
				if(fax==fay)
				{
					cout<<"NO"<<endl;
					flag=1;
					break;
				}
				unit(i,j+m),unit(j,i+m);
			}
		}
		if(!flag)cout<<"YES"<<endl;
	}
}