开店 BZOJ 4012
开店
【问题描述】
风见幽香有一个好朋友叫八云紫,她们经常一起看星星看月亮从诗词歌赋谈到人生哲学。最近她们灵机一动,打算在幻想乡开一家小店来做生意赚点钱。这样的想法当然非常好啦,但是她们也发现她们面临着一个问题,那就是店开在哪里,面向什么样的人群。很神奇的是,幻想乡的地图是一个树形结构,幻想乡一共有 n个地方,编号为 1 到 n,被 n-1 条带权的边连接起来。每个地方都住着一个妖怪,其中第 i 个地方的妖怪年龄是 x_i。妖怪都是些比较喜欢安静的家伙,所以它们并不希望和很多妖怪相邻。所以这个树所有顶点的度数都小于或等于 3。妖怪和人一样,兴趣点随着年龄的变化自然就会变化,比如我们的 18 岁少女幽香和八云紫就比较喜欢可爱的东西。幽香通过研究发现,基本上妖怪的兴趣只跟年龄有关,所以幽香打算选择一个地方 u(u为编号),然后在 u开一家面向年龄在 L到R 之间(即年龄大于等于 L、小于等于 R)的妖怪的店。也有可能 u这个地方离这些妖怪比较远,于是幽香就想要知道所有年龄在 L 到 R 之间的妖怪,到点 u 的距离的和是多少(妖怪到 u 的距离是该妖怪所在地方到 u 的路径上的边的权之和) ,幽香把这个称为这个开店方案的方便值。幽香她们还没有决定要把店开在哪里,八云紫倒是准备了很多方案,于是幽香想要知道,对于每个方案,方便值是多少呢。
【输入格式】
第一行三个用空格分开的数 n、Q和A,表示树的大小、开店的方案个数和妖怪的年龄上限。
第二行n个用空格分开的数 x_1、x_2、…、x_n,x_i 表示第i 个地点妖怪的年龄,满足0<=x_i<A。(年龄是可以为 0的,例如刚出生的妖怪的年龄为 0。)
接下来 n-1 行,每行三个用空格分开的数 a、b、c,表示树上的顶点 a 和 b 之间有一条权为c(1 <= c <= 1000)的边,a和b 是顶点编号。
接下来Q行,每行三个用空格分开的数 u、 a、 b。对于这 Q行的每一行,用 a、b、A计算出 L和R,表示询问“在地方 u开店,面向妖怪的年龄区间为[L,R]的方案的方便值是多少”。
对于其中第 1 行,L 和 R 的计算方法为:L=min(a%A,b%A), R=max(a%A,b%A)。
对于第 2 到第 Q 行,假设前一行得到的方便值为 ans,那么当前行的 L 和 R 计算方法为: L=min((a+ans)%A,(b+ans)%A), R=max((a+ans)%A,(b+ans)%A)。
【输出格式】
对于每个方案,输出一行表示方便值。
【样例输入】
10 10 10
0 0 7 2 1 4 7 7 7 9
1 2 270
2 3 217
1 4 326
2 5 361
4 6 116
3 7 38
1 8 800
6 9 210
7 10 278
8 9 8
2 8 0
9 3 1
8 0 8
4 2 7
9 7 3
4 7 0
2 2 7
3 2 1
2 3 4
【样例输出】
1603
957
7161
9466
3232
5223
1879
1669
1282
0
【数据范围】
满足 n<=150000,Q<=200000。对于所有数据,满足 A<=10^9
题解:
画图分析可知:
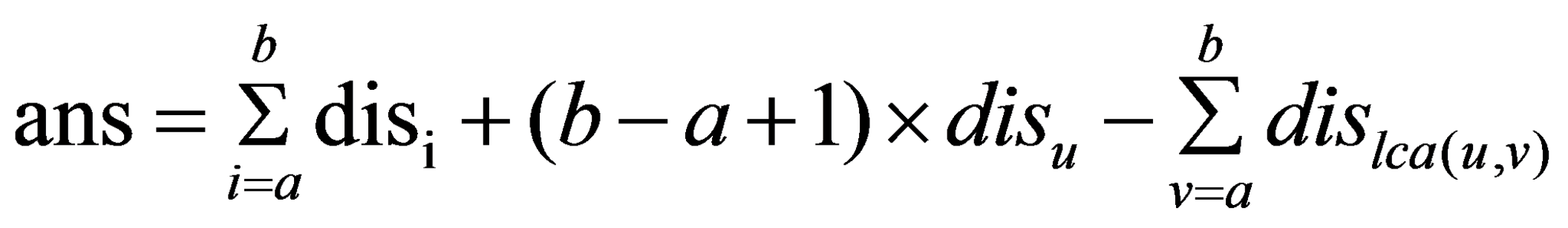
其中dis表示点到根的距离,区间[a,b]表示在要求年龄范围内的点,lca(u,v)表示点u和点v的最近公共祖先
点u的所有祖先都在根到u的路径上,点v同样
那么树链剖分+可持久化线段树
以dfs序建立线段树
将每个点按年龄顺序加入
在树剖往上跳的过程中,覆盖祖先到它的区间,表示有一个点经过这些点
用前缀和处理出这一段区间的边权和(边为它父亲连向它的边),就可以区间加了
查询时第一部分也也用前缀和维护,第二部分直接求,第三部分用可持久化线段树
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdlib>
5 #include<cstdio>
6 #include<cmath>
7 using namespace std;
8 typedef long long lol;
9 inline int Get()
10 {
11 int x;
12 char c;
13 while((c = getchar()) < '0' || c > '9');
14 x = c - '0';
15 while((c = getchar()) >= '0' && c <= '9') x = x * 10 + c - '0';
16 return x;
17 }
18 const int me = 1000233;
19 const int inf = 2147483647;
20 struct point
21 {
22 int id, age;
23 };
24 point dot[me];
25 inline bool operator < (const point &a, const point &b)
26 {
27 if(a.age != b.age) return a.age < b.age;
28 return a.id < b.id;
29 }
30 int n, q;
31 int root;
32 int rt[me];
33 int tot, to[me], fir[me], nex[me];
34 lol mo;
35 lol val[me];
36 inline void Ins(const int &x, const int &y, const int &z)
37 {
38 nex[++tot] = fir[x];
39 fir[x] = tot;
40 to[tot] = y;
41 val[tot] = z;
42 }
43 int stamp;
44 int si[me], pos[me], top[me], son[me], fat[me], last[me];
45 lol dis[me];
46 void Chain_one(const int &u)
47 {
48 si[u] = 1;
49 for(int i = fir[u]; i; i = nex[i])
50 {
51 int v = to[i];
52 if(v == fat[u]) continue;
53 fat[v] = u;
54 last[v] = val[i];
55 dis[v] = dis[u] + val[i];
56 Chain_one(v);
57 si[u] += si[v];
58 if(si[son[u]] < si[v]) son[u] = v;
59 }
60 }
61 lol sum_dis[me], sum_edge[me];
62 void Chain_two(const int &u)
63 {
64 pos[u] = ++stamp;
65 sum_edge[stamp] = last[u];
66 if(son[u])
67 {
68 top[son[u]] = top[u];
69 Chain_two(son[u]);
70 }
71 for(int i = fir[u]; i; i = nex[i])
72 {
73 int v = to[i];
74 if(v == son[u] || v == fat[u]) continue;
75 top[v] = v;
76 Chain_two(v);
77 }
78 }
79 int lc[10000233], rc[10000233];
80 lol sum[10000233], cnt[10000233];
81 int Modify(const int &y, const int &l, const int &r, const int &a, const int &b)
82 {
83 int x = ++tot;
84 lc[x] = lc[y];
85 rc[x] = rc[y];
86 sum[x] = sum[y];
87 cnt[x] = cnt[y];
88 if(a == l && b == r)
89 {
90 ++cnt[x];
91 return x;
92 }
93 sum[x] += sum_edge[b] - sum_edge[a - 1];
94 int mi = l + r >> 1;
95 if(a > mi) rc[x] = Modify(rc[x], mi + 1, r, a, b);
96 else
97 if(b <= mi) lc[x] = Modify(lc[x], l, mi, a, b);
98 else
99 lc[x] = Modify(lc[x], l, mi, a, mi), rc[x] = Modify(rc[x], mi + 1, r, mi + 1, b);
100 return x;
101 }
102 lol Query(const int &x, const int &l, const int &r, const int &a, const int &b)
103 {
104 lol res = (sum_edge[b] - sum_edge[a - 1]) * cnt[x];
105 if(a == l && b == r) return res + sum[x];
106 int mi = l + r >> 1;
107 if(a > mi) return res + Query(rc[x], mi + 1, r, a, b);
108 if(b <= mi) return res + Query(lc[x], l, mi, a, b);
109 return res + Query(lc[x], l, mi, a, mi) + Query(rc[x], mi + 1, r, mi + 1, b);
110 }
111 inline int Add(int x)
112 {
113 while(top[x] != 1)
114 {
115 root = Modify(root, 1, n, pos[top[x]], pos[x]);
116 x = fat[top[x]];
117 }
118 root = Modify(root, 1, n, pos[top[x]], pos[x]);
119 return root;
120 }
121 inline lol Ask(const int &rt, int x)
122 {
123 lol res = 0;
124 while(top[x] != 1)
125 {
126 res += Query(rt, 1, n, pos[top[x]], pos[x]);
127 x = fat[top[x]];
128 }
129 return res + Query(rt, 1, n, pos[top[x]], pos[x]);
130 }
131 int main()
132 {
133 n = Get(), q = Get(), mo = Get();
134 for(int i = 1; i <= n; ++i) dot[i] = (point) {i, Get()};
135 sort(dot + 1, dot + 1 + n);
136 for(int i = 1; i < n; ++i)
137 {
138 int x, y, z;
139 x = Get(), y = Get(), z = Get();
140 Ins(x, y, z);
141 Ins(y, x, z);
142 }
143 Chain_one(1);
144 top[1] = 1;
145 Chain_two(1);
146 for(int i = 1; i <= n; ++i)
147 {
148 sum_edge[i] += sum_edge[i - 1];
149 sum_dis[i] = sum_dis[i - 1] + dis[dot[i].id];
150 }
151 tot = 0;
152 for(int i = 1; i <= n; ++i) rt[i] = Add(dot[i].id);
153 lol ans = 0;
154 while(q--)
155 {
156 lol u = Get(), a = Get(), b = Get();
157 a = (a + ans) % mo;
158 b = (b + ans) % mo;
159 if(a > b) swap(a, b);
160 a = lower_bound(dot + 1, dot + 1 + n, (point) {0, a}) - dot;
161 b = upper_bound(dot + 1, dot + 1 + n, (point) {inf, b}) - dot - 1;
162 lol c, d;
163 c = Ask(rt[a - 1], u);
164 d = Ask(rt[b], u);
165 ans = sum_dis[b] - sum_dis[a - 1] + (b - a + 1) * dis[u] - ((d - c) << 1);
166 printf("%lld\n", ans);
167 }
168 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号