小波变换和傅里叶变换的区别
引自：https://www.cnblogs.com/Sweepingmonk/p/11584913.html
1. 应用范围
- 高维数据因为其计算代价昂贵（纬度高计算必然昂贵）和建立索引结构的困难（空间索引结构往往面临着“维度灾”），因此有对其进行数据压缩的需求，即对高维数据进行降维，傅里叶变换和小波变换都可以用来做这件事
2. 傅里叶变换
- 傅里叶变换，可以理解为将一个函数映射到（L2空间的）某组基上。观察这组基(严格来说不是一组基)cosx,sinx,cos2x,sin2x...发现有个特点是它可以由一个母函数cosx通过平移和缩放获得。
-
用不同频率的三角函数去拟合原始信号
- 而原始信号中的主要信息都集中在低频分量上，高频分量往往是噪音，因此我们可以对变换后的三角函数系数只保留其前k个系数，而忽略剩余的高频部分，这样就将数据降为了k维，由于高频大多是噪音，因此丢失信息并不多。（实现数据降维）
- 假设傅里叶变换f(x)=a1cos(x)+b1sin(x)+a2cos(2x)+b2sin(2x)+...+akcos(kx)+bksin(kx)已经能满足精度要求了（再往后的高频都是噪声了），可以发现每个映射的分量都是在几乎全定义域有非零值。
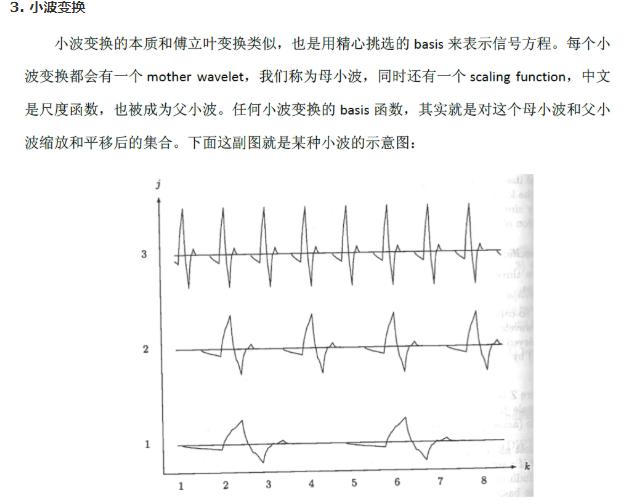
-所谓“小波函数”是一族函数，需要满足 1.均值为0；2.在时域和频域都局部化（不是蔓延整个坐标轴的），满足这两条的函数就是小波函数，有很多，最简单的是Haar Wavelet。所以小波分析或者说小波变换要做的就是将原始信号表示为 一组小波基的线性组合，然后通过忽略其中不重要的部分达到数据压缩或者说降维的目的。
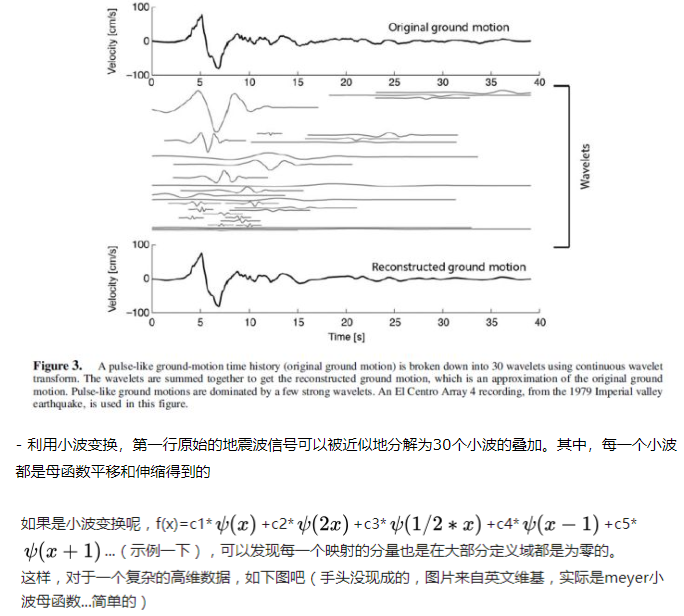
- 而原始信号中的主要信息都集中在低频分量上，高频分量往往是噪音，因此我们可以对变换后的三角函数系数只保留其前k个系数，而忽略剩余的高频部分，这样就将数据降为了k维，由于高频大多是噪音，因此丢失信息并不多。（实现数据降维）
- 假设傅里叶变换f(x)=a1cos(x)+b1sin(x)+a2cos(2x)+b2sin(2x)+...+akcos(kx)+bksin(kx)已经能满足精度要求了（再往后的高频都是噪声了），可以发现每个映射的分量都是在几乎全定义域有非零值。
