\(\mathrm{Part\ 0}\) 前言
学习这玩意是因为补题 IOI2022 集训队互测 Day5T2。
题面是这样的:
现有 \(k\) 个人,你可以举办任意多次由三个人参加的聚会,现要求任意两个人都同时参加聚会恰好一次,试构造一组聚会方案。
可以说明,在给定的范围内一定有解。
一行一个正整数 \(k(1\le k \le 3000)\),保证 \(k \bmod 6\) 为 \(1\) 或 \(3\)。
vp 时只写了前面的 \(k=2^t-1,k=3^t\) 十分就转头去冲 T3 了。补题时 wwc 的题解看起来实在让人太头大了,补题极其困难。
学长找到了一份名字叫 sts 的课件,于是我点开来看,是一份英文课件,直到看完这份课件,我终于会了这道题。觉得这道题很有意思,于是写了这篇博文。
本文的内容大部分来源于此英文课件,但由于我并不知道其具体出处,无法在此标注。
\(\mathrm{Part\ 1}\) 施泰纳三元系
一个 Steiner 三元系由一个集合 \(S\) 和一个三元组集合 \(T\) 组成。满足 \(S\) 中每对元素都在 \(T\) 中出现且出现次数为 \(1\) 。
比如 \(S=\{0,1,2\},T=\{(0,1,2)\}\);\(S=\{0,1,2,3,4,5,6\},T = \{(0,1,3), (1,2,4), (2,3,5), (3,4,6), (4,5,0), (5,6,1), (6,0,2)\}\)。
容易算出如果 \(|S|=v\) 那么 \(|T|=\frac{v(v-1)}{6}\)。
关于它的一个结论是,\(T\) 存在当且仅当 \(v\equiv1\ \text{or}\ 3\bmod6\)。
因为包含 \(x\) 的三元组将 \((i,x)\) 这些二元组两两配对,所以 \(v-1\) 只能是偶数,那么 \(v\) 只能是奇数。
当 \(v=6n+5\) 时,\(v(v-1)=(36n^2+54n+20)\bmod 6\not\equiv0\)。所以 \(v\) 不能为 \(6n+5\)。
当 \(v=6n+1\ \text{or}\ +3\) 时易证 \(v(v-1)\bmod 6=0\) 。而这个结论剩下的部分需要我们通过构造证明。
\(\mathrm{Part\ 2}\) 拟群、拉丁方阵
拉丁方阵是一个 \(n\times n\) 的方阵。它满足每行每列 \(1\sim n\) 每个数只出现一次。
例如 \(n=3\) 时的一种拉丁方阵为:
123
231
312
求一个拉丁方阵非常容易,最常用的方法是对于每个数,随机选取方阵中一个空的格子,初始位置是 \((x,y)\) 然后固定每次的移动是 \(delx=1/-1,dely=1/-1\)。然后不断填充。
拟群(quasi-group)是一种代数系统。
拟群由一个集合 \(S\) 和一个二元运算 \(\otimes\) 组成。
满足以下两个条件:
-
\(a \otimes b \in S(a\in S,b\in S)\)。
-
\(a \otimes x=b,y\otimes a=b\) 这两个方程只有唯一的 \(x,y\) 解。
举个例子 \(S={0,1,2}, a\otimes b=2\times a+b+1\)。
| \(\otimes\) | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 1 | 2 | 0 |
| 1 | 0 | 1 | 2 |
| 2 | 2 | 0 | 1 |
幂等拟群是指满足 \(a \otimes a=a (a\in S)\) 的拟群。
一个拟群是可交换的是指满足 \(a\otimes b=b\otimes a(a,b\in S)\) 的拟群。
看到这里也许你会发现,拟群的乘法表实际上就是一个拉丁方阵。
而幂等拟群可以用一个满足 \(a_{x,x}=x\) 的拉丁方阵表示。
而可交换这一性质可以由 \(a_{x,y}=a_{y,x}\) 来体现。
当 \(n\) 为奇数的时候,我们是可以构造一个可交换的幂等拟群的,具体形状如下:
\(n=3:\)
1 3 2
3 2 1
2 1 3
\(n=5:\)
1 4 2 5 3
4 2 5 3 1
2 5 3 1 4
5 3 1 4 2
3 1 4 2 5
可以发现我们只要选取的初始位置是主对角线上 \((i,i)\) 的位置然后向右上方填充即可。
\(n\) 为偶数呢?很抱歉,我们构造不出来。原因很简单,一个可交换的幂等拟群中一个元素的出现次数必然是奇数次 ( 对角线上一次+矩阵中 \(2x\) 次 )。
好了,至此我们可以得出一个 \(v=6n+3\) 时的做法了。
\(\mathrm{Part\ 3}\) 关于 \(v=6n+3\) 的构造方法
我们将 \(1\sim v\) 划分成三组,每组 \(m=2n+1\) 个元素。
设 \(g(i,j)\) 表示第 \(j\) 组的第 \(i\) 个元素。接下来我们构造如下两种三元组:
- \(\{g(i,0),g(i,1),g(i,2)\}\ (1\leq i\leq m)\)。
- \(\{g(i,k),g(j,k),g(i\otimes j,(k+1)\bmod 3)\}\ (1\leq i< j\leq m,0\leq k<3)\)。
可以用如下一张图来解释:
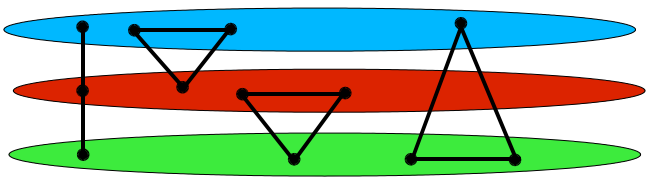
这种构造的正确性证明:
首先来计算三元组总数,第一种三元组有 \(\frac{v}{3}\) 个,第二种有 \(\frac{v\times(v-3)}{6}\) 个,加起来是 \(\frac{v\times(v-1)}{6}\) 个。
接下来只要证明每对元素都在其中出现过即可。
(下文 \(b\) 和 \(d\) 均为模 \(3\) 意义下的值)
对于 \(g(a,b)\) 和 \(g(c,d)\) 两个元素,如果 \(a=c\) 那么显然出现过,如果 \(a \not = c\) ,假设 \(d=b+1\) 根据 \(a\otimes x=c\) 的解唯一,且易知 \(x\not =a\) 所以必定在第三种出现。
所以在代码实现中,我们只需要构造一个 可交换的幂等拟群的乘法表(拉丁方阵),然后构造如上的三元组即可。代码难度很小。
\(\mathrm{Part\ 4}\) 可交换的半幂等拟群
上文已经提到过,\(n\) 为偶数的时候我们不能构造出可交换的幂等拟群。
但是,我们可以构造出半幂等拟群。
半幂等拟群指满足 \(a\otimes a=(a+\frac{n}{2})\otimes (a+\frac{n}{2})=a (1\leq a\leq \frac{n}{2})\) 的拟群。
\(n=4:\)
1 3 2 4
3 2 4 1
2 4 1 3
4 1 3 2
\(n=6:\)
1 4 2 5 3 6
4 2 5 3 6 1
2 5 3 6 1 4
5 3 6 1 4 2
3 6 1 4 2 5
6 1 4 2 5 3
构造方法是,对于前 \(\frac{n}{2}\) 个数在主对角线上一次构造,后 \(\frac{n}{2}\) 个数在主对角线下一斜构造。
\(\mathrm{Part\ 5}\) 关于 \(v=6n+1\) 的构造方法
我们将前 \(6n\) 个元素分成三组,每组 \(2n\) 个元素。最后一个元素 \(v\) 不参与分组。
设 \(g(i,j)\) 表示第 \(j\) 组的第 \(i\) 个元素。接下来我们构造如下三种三元组:
-
\(\{g(i,0),g(i,1),g(i,2)\}\ (1\leq i\leq n)\),注意这里是 \(n\)。
-
\(\{v,g(i,k),g(n+i,(k-1)\bmod 3)\}\ (1\leq i\leq n,0\leq k<3)\)。
-
\(\{g(i,k),g(j,k),g(i\otimes j,(k+1)\bmod 3)\}\ (1\leq i< j\leq 2n,0\leq k<3)\)。
同样来分析下正确性:
第一种三元组个数为 \(3n\) 个,第二种为 \(3n\) 个,第三种为 \(6n^2 – 3n\) 个,加起来是 \(\frac{v(v-1)}{6}\) 个。
接下来只要证明每对元素都在其中出现过即可。
(下文 \(b\) 和 \(d\) 均为模 \(3\) 意义下的值)
当其中一个元素是 \(v\) 时,显然在第二种出现过。
对于 \(g(a,b)\) 和 \(g(c,d)\) 两个元素,如果 \(a=c\) ,当 \(a\leq n\) 时在第一种中出现过,否则的话根据上面 Part 3 的分析方法总会在第三种出现。
如果 \(a>n,c=a-n\) ,那么如果 \(b=d\),他们会在第三种出现。如果 \(b\not =d\),假设 \(d=b+1\),那么因为 \(a\otimes x=c\) 的 \(x\) 一定为 \(a\) 所以他并不会在第三种三元组出现而是在第二种中出现。
其他情况均可类似证明在第三种出现过。
所以在代码实现中,我们只需要构造一个 可交换的半幂等拟群的乘法表(拉丁方阵),然后构造如上的三元组即可。代码难度同样很小。
\(\mathrm{Part\ 6}\) 代码实现和个人想法
这题在构造时需要充分利用拟群的定义才能得出思路,包括 \(k=3^t\) 的部分分也需要与拟群类似的思想结合分治才能构造出来。个人感觉是一道很好玩的题。
#include<bits/stdc++.h>
#define poly vector<int>
#define IOS ios::sync_with_stdio(false)
#define ll long long
#define mp make_pair
#define mt make_tuple
#define pa pair < int,int >
#define fi first
#define se second
#define inf 1e18
#define mod 998244353
//#define int ll
#define N 3005
using namespace std;
inline char gc(){static char buf[1000000],*p1=buf,*p2=buf;return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;}
#define gc getchar
inline ll read(){char c=gc();ll su=0,f=1;for (;c<'0'||c>'9';c=gc()) if (c=='-') f=-1;for (;c>='0'&&c<='9';c=gc()) su=su*10+c-'0';return su*f;}
inline void write(ll x){if (x<0){putchar('-');write(-x);return;}if (x>=10) write(x/10);putchar(x%10+'0');}
inline void writesp(ll x){write(x),putchar(' ');}
inline void writeln(ll x){write(x);putchar('\n');}
int id[N][5];
int p;
int a[N][N];
int n;
vector<tuple<int,int,int>>ans;
void Init(int x)//构造可交换的幂等拟群
{
for (int i=1;i<=x;i++)
for (int j=1;j<=3;j++)
id[i][j]=(i-1)*3+j;
for (int i=1;i<=x;i++)
{
int nowx=i,nowy=i;
while (!a[nowx][nowy])
{
a[nowx][nowy]=i;
nowx--;
nowy++;
if (nowx==0) nowx=x;
if (nowy==x+1) nowy=1;
}
}
}
void Init1(int x)//构造可交换的半幂等拟群
{
for (int i=1;i<=x;i++)
for (int j=1;j<=3;j++)
id[i][j]=(i-1)*3+j;
p=n;
for (int i=1;i<=x/2;i++)
{
int nowx=i,nowy=i;
while (!a[nowx][nowy])
{
a[nowx][nowy]=i;
nowx--;
nowy++;
if (nowx==0) nowx=x;
if (nowy==x+1) nowy=1;
}
}
for (int i=x/2+1;i<=x;i++)
{
int nowx=i-x/2+1,nowy=i-x/2;
while (!a[nowx][nowy])
{
a[nowx][nowy]=i;
nowx--;
nowy++;
if (nowx==0) nowx=x;
if (nowy==x+1) nowy=1;
}
}
}
void outp()
{
for (auto u:ans) writesp(get<0>(u)),writesp(get<1>(u)),writeln(get<2>(u));
}
void BellaKira()
{
n=read();
if (n%6==3)
{
Init(n/3);
for (int i=1;i<=n/3;i++)
for (int j=i;j<=n/3;j++)
{
if (i==j)
ans.push_back(mt(id[i][1],id[i][2],id[i][3]));
else
{
for (int k=1;k<=3;k++)
ans.push_back(mt(id[i][k],id[j][k],id[a[i][j]][(k)%3+1]));
}
}
outp();
} else
{
Init1((n-1)/3);
for (int i=1;i<=n/3;i++)
{
for (int j=i;j<=n/3;j++)
{
if (i==j&&i<=n/6)
ans.push_back(mt(id[i][1],id[i][2],id[i][3]));
else
if (i!=j)
{
for (int k=1;k<=3;k++)
ans.push_back(mt(id[i][k],id[j][k],id[a[i][j]][(k)%3+1]));
}
}
if (i<=n/6)
{
for (int k=1;k<=3;k++)
ans.push_back(mt(p,id[i][k],id[n/6+i][(k-1+3-1)%3+1]));
}
}
outp();
}
}
signed main()
{
int T=1;
while (T--)
{
BellaKira();
}
}
/*
*/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号