题解 | luoguP6491 [COCI 2010/2011 #6] ABECEDA

trie 树建图 floyd 最长路

正文：

容易知道它让我们求的是一个各个字符的总体大小顺序，这个东西在知道一定量的基础大小关系后是可以用 floyd 跑最长路求解的，下面给出解析。

---

Trie 树求基础大小关系：

看到按照某种字典序排列，首先要了解字典序排列是怎么排的，我们认为读者都知道是怎么排的，就直接列出一个要用的事实。

• 前 \(n\) 个字符相等的 \(m\) 个字符串的第 \(n+1\) 个字符的大小关系为其字符串的排名从大到小。

而我们可以将字符串按照输入的顺序插入 Trie，每建一个新节点就意味着新节点代表的字符要小于这个新节点的父亲节点插入的上一个儿子节点的字符，可以用这个得到一些基础的大小关系。

以样例为例，如下图：

1. 插入 ula。
   
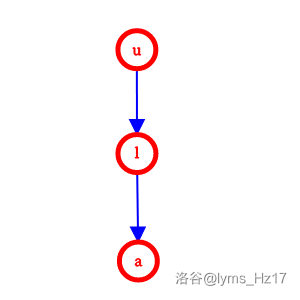
   没有得到任何大小关系。

2. 插入 uka。
   
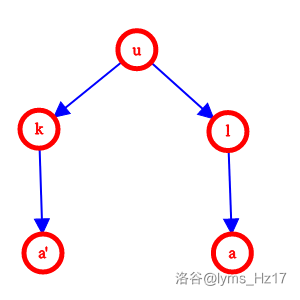
   得到了 \(l < k\)。

以此类推便可以得到所有基础大小关系。

这里给出示例代码：

struct node {
    int ch[27], lasch;
} t[26 * 1001];
int cnt = 1;

inline void insert(string a) {
    int p = 1;
    for(uint i = 0; i < a.size(); i ++) {
        int c = a[i] - 'a' + 1; // 加一是和 0 区分
        if(t[p].ch[c]) p = t[p].ch[c];
        else {
            if(t[p].lasch) {
                dis[t[p].lasch][c] = e[t[p].lasch][c] = 1; // 这里建立大小关系
                if(e[c][t[p].lasch]) {
                    putchar('!');
                    exit(0);
                }
            }
            t[p].lasch = c; // 记录上一个
            p = t[p].ch[c] = ++cnt;
        }
    }
}

---

floyd 求总大小关系

我们已经了解了一些字符之间的基础大小关系，那么就来扩展它们。举几个例子看一下吧。

如 \(a > b\)，\(b > c\) 的简单关系。我们可以建图，建立以大小关系连接的边权为 \(1\) 的有向图，如下。

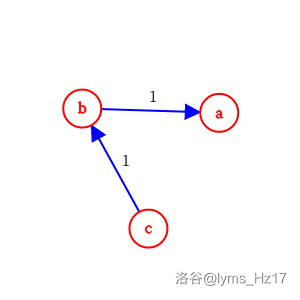
从 \(c\) 到 \(a\) 的最长路径为 \(2\)，这是所有到达 \(a\) 的路径中的最长路，容易注意到，这个 \(2\) 也是所有小于 \(a\) 的字符的数量。

再看无解的情况，如 \(a > b\)，\(b > c\)，\(b > c\)，如图。

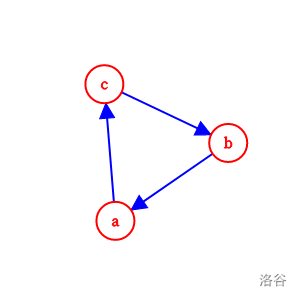
容易发现出现了环。

最后是多组解的情况，如 \(a > b\)，\(c > b\)。

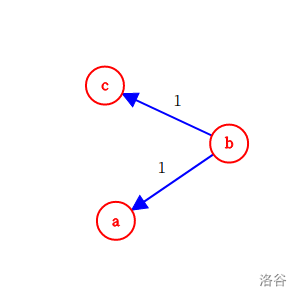
发现到达 \(a\)、\(c\) 的最长路长度相同，都为 \(1\)。

稍微推广，我们就可以得到以下几个事实。

1. 对于任意点 \(x\)，到达 \(x\) 的所有路径中的最长路经长度为点 \(x\) 的排名数 \(-1\)。
2. 若图中存在环，或者说出现了最长路长度为无限的情况，这意味着一个数以某种传递方式大于了自己，也就是无解了。
3. 通过以上方式求出的每个点的排名都是唯一的，如果不唯一就意味着存在多组解，无法得到整体的大小关系。

故跑完 floyd 就可以得到总体大小关系。

这里给出示例代码：

for(int k = 1; k <= 26; k ++) {
    for(int i = 1; i <= 26; i ++) // 求最长路
        for(int j = 1; j <= 26; j ++) 
            if(i != j and k != i and k != j) 
                if(dis[k][j] and dis[i][k] and dis[i][j] < dis[i][k] + dis[k][j]) 
                    dis[i][j] = dis[i][k] + dis[k][j];

    for(int i = 1; i <= k; i ++) // 判断环
        for(int j = 1; j <= k; j ++) 
            if(dis[i][j] and e[j][k] and e[k][i]) {
                putchar('!');
                exit(0);
            }
}
int rk[27] = {}; // 记录排名
for(int i = 1; i <= 26; i ++) {
    for(int j = 1; j <= 26; j ++)
        if(hs[i]) // hs 代表某字符是否出现过
            rk[i] = max(rk[i], dis[i][j] + 1);
}

---

虽然把上面代码拼起来再写两笔就是完整代码但是我就是要单独贴出来完整代码。

完整代码（有注释）：

// code by 樓影沫瞬_Hz17
#include <bits/stdc++.h>
#define int long long
#define en_ putchar('\n')
#define e_ putchar(' ')
using namespace std;
inline int in() { 
    int n = 0, p = getchar();
    while (p < '-')p = getchar();
    bool f = p == '-' ? p = getchar() : 0; //
    do n = n * 10 + (p ^ 48), p = getchar();
    while (isdigit(p));
    return f ? -n : n; //
    return n;
}
inline int in(int &a) { return a = in(); }
inline void out(int n) {
    if(n < 0) putchar('-'), n = -n;
    if(n > 9) out(n / 10);
    putchar(n % 10 + '0');
}

int n;
int hs[27]; // 记录某字母是否出现
string a[101]; // 字符串

struct node {
    int ch[27], lasch;
} t[26 * 1001]; // trie 结构体
int cnt = 1;
int dis[27][27], e[27][27]; // 记录边和最长路

inline void insert(string a) { // 见上文，不赘述
    int p = 1;
    for(uint i = 0; i < a.size(); i ++) {
        int c = a[i] - 'a' + 1;
        if(t[p].ch[c]) p = t[p].ch[c];
        else {
            if(t[p].lasch) {
                dis[t[p].lasch][c] = e[t[p].lasch][c] = 1;
                if(e[c][t[p].lasch]) {
                    putchar('!');
                    exit(0);
                }
            }
            t[p].lasch = c;
            p = t[p].ch[c] = ++cnt;
        }
    }
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("i", "r", stdin); // 自动关 freopen 说是
#endif
    in(n);
    for(int i = 1; i <= n; i ++) 
        cin >> a[i], insert(a[i]);
    for(int i = 1; i <= n; i ++) {
        int r = a[i].size() - 1;
        for(int j = 0; j <= r; j ++) 
            hs[a[i][j] - 'a' + 1] = 1;
    } // 就只是读入（我话好多）
    for(int k = 1; k <= 26; k ++) { // 见上文，不赘述
        for(int i = 1; i <= 26; i ++) 
            for(int j = 1; j <= 26; j ++) 
                if(i != j and k != i and k != j) 
                    if(dis[k][j] and dis[i][k] and dis[i][j] < dis[i][k] + dis[k][j]) 
                        dis[i][j] = dis[i][k] + dis[k][j];

        for(int i = 1; i <= k; i ++) 
            for(int j = 1; j <= k; j ++) 
                if(dis[i][j] and e[j][k] and e[k][i]) {
                    putchar('!');
                    exit(0);
                }
    }
    int rk[27] = {}; 
    for(int i = 1; i <= 26; i ++) {
        for(int j = 1; j <= 26; j ++)
            if(hs[i])
                rk[i] = max(rk[i], dis[i][j] + 1);
    }
    int ans[27] = {};
    // 下面是输出
    for(int i = 1; i <= 26; i ++) { 
        if(ans[rk[i]] and rk[i]) { // 如果有相同排名的就是多组解
            putchar('?');
            exit(0);
        }
        ans[rk[i]] = i;
    }
    stack<char> tans;
    for(int i = 1; i <= 26; i ++) {
        if(!ans[i]) break;
        tans.push(ans[i] + 'a' - 1);
    } 
    while(!tans.empty()) {
        putchar(tans.top());
        tans.pop();
    }
}
// 星間~ 干渉~ 融解~ 輪迴~ 邂逅~ 再生~ ララバイ~
// 这一句是给注释的注释：多次元宇宙融合論豪庭！！！

时间复杂度：

令 \(N\) 为输入字符总数，\(M\) 为字母数（即 \(26\)）。
复杂度为 \(O(N + M ^ 3)\)。