堆排序的时间复杂度分析

本文包括堆排序的代码、例子（图示）、时间复杂度分析 

 

#define MAXSIZE 10000

/*全局变量，需要排序的数组*/
long long int num[MAXSIZE];

/*对非叶子结点和它的孩子结点进行调整，使其重新成为大根堆，用于堆排序*/
void NodeSort(long long int node,long long int len)
{
    long long int left = node * 2 + 1, right = left + 1, max_node = left;
    while (left < len)
    {
        if (right < len && num[left] < num[right])            
                max_node = right;
        if (num[node] < num[max_node])
        {
            swap(node, max_node);
            node = max_node;
            left = node * 2 + 1;
            right = left + 1;
            max_node = left;
        }
        else
            return;
    }
}

/*堆排序*/
void HeapSort(long long int len)
{
    while (len != 0)
    {
        for (long long int i = len; i > 0; i -= 2)//将非叶子结点依次进行调整，保证每次for循环结束之后都是大根堆
            NodeSort((i - 1) / 2, len);
        swap(len - 1, 0); //首尾元素交换       
        len--;//对除了最后一个元素外的数组继续进行排序
    }
}

 

 

例子图示：

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

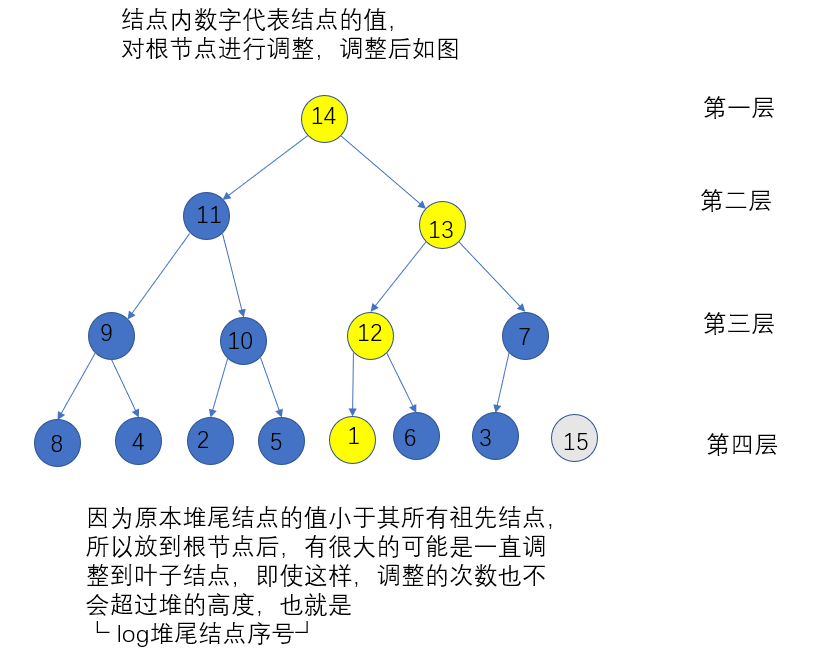
 之后按照上述的调整堆的方式，不断进行调整，直到堆只剩下根节点的时候，数组有序

 

下面的一些计算可以代入上面的例子理解

 

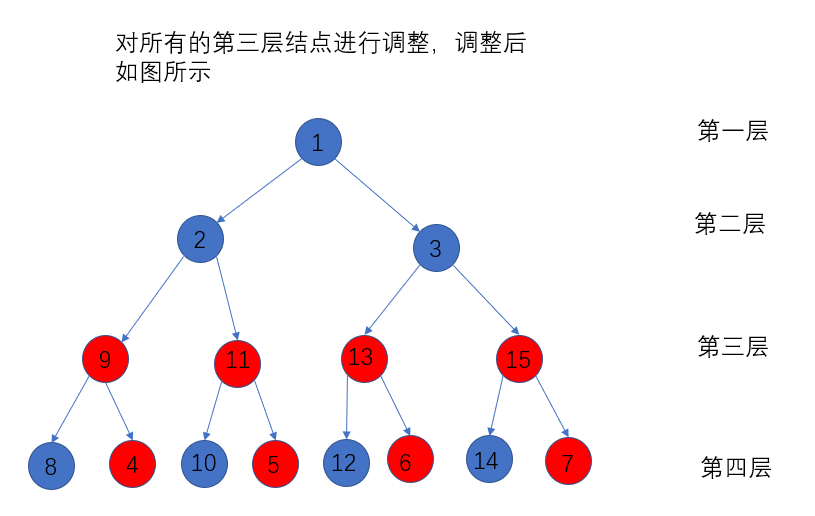
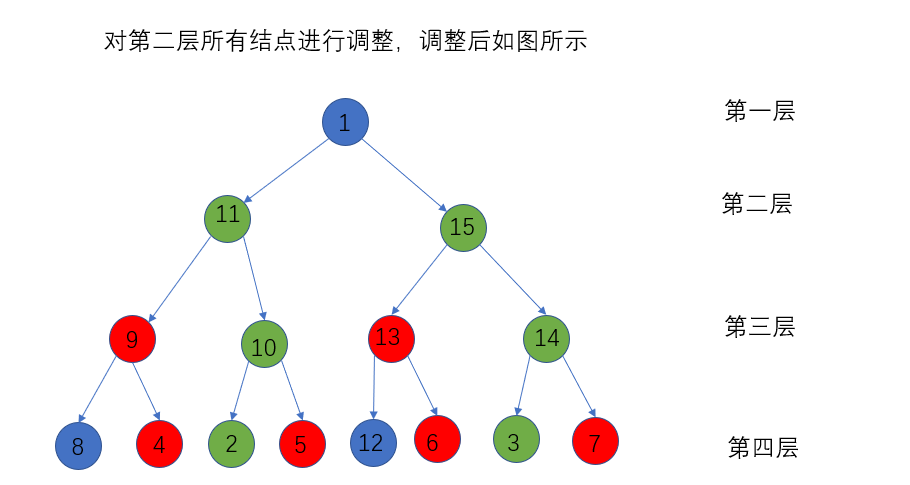
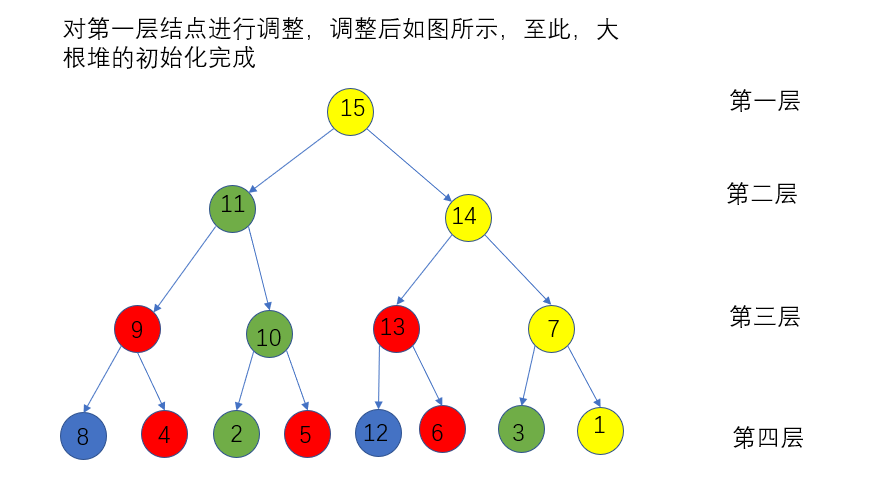
堆排序分为两步，即初始化堆、调整堆。

 

两个步骤都要调用一个调整结点顺序的函数NodeSort，以大根堆为例，操作为：

1：如果父亲结点num[a]和它的两个孩子结点num[2a+1], num[2a+2]满足um[a] > max{num[2a+1], num[2a+2]}，那么返回；

2：如果不满足堆的性质，那么将父亲结点num[a]和较大孩子结点max{num[2a+1], num[2a+2]}交换，

3：将原来较大的孩子结点作为父亲结点，重复上述操作，直到孩子结点是叶子结点为止

 

初始化堆的时间复杂度分析

初始化堆的时候，对于每个非叶子结点，都要调用上述函数，将它与它的孩子结点进行比较和交换，顺序是从后向前。

以操作2作为基本操作，对每一层都完全铺满的堆进行分析，

设元素个数为n，则堆的高度k=log（n+1）≈log n，非叶子结点的个数为2^（k-1）-1

假设每个非叶子结点都需要进行调整，则第i层的非叶子结点需要的操作次数为k-i，

第i层共有2^（i-1）个结点，则第i层的所有结点所做的操作为k*2^（i-1）- i*2^（i-1），

共k-1层非叶子结点，总的操作次数为 

　　　　

 

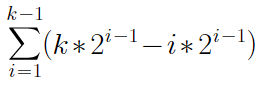
化简可得，上式=2^k-k+1，将k=log（n+1）≈log n代入，得n - log n +1，

所以，初始化堆的复杂度为O(n)

 

调整堆的时间复杂度分析

调整堆的复杂度计算和初始化堆差不多，

假设根节点和排在最后的序号为m的叶子结点交换，并进行调整，那么调整的操作次数 = 原来m结点所在的层数 = 堆的高度（因为m结点在堆的最后）= log m

共n个结点，调整的总操作次数为

　　　　　

 

化简可得，上式=log (n-1)! ≈ n*log n

 所以，调整堆的复杂度为O(n*log n)

 

所以，总体复杂度为O(n*log n)