CF234G Practice

这道题其实挺难想的，我最开始想的是 \(n-1\) 的构造方式，再加上好损友的亿点提示（关键部分没听他的），接着是 \(\dfrac{n}{2}\) 的构造，最后才是正解 \(\lceil \log _2 n \rceil\)

题目传送门

题意

现在有 \(n\) 个人进行比赛（编号从 \(1\) 到 \(n\)），每次把这 \(n\) 个人不遗漏地分成两队进行比赛。

请构造一种比赛方式，使得比赛次数尽可能少，并且每两个人之间都在不同队比赛过。

思路

首先，最简单的思路就是，\(n-1\) 轮，每个人和其他没有和他比过赛的人比赛。

很明显，这不是最优的。

接着，考虑优化。（中间 \(\dfrac{n}{2}\) 的想法忘了咋搞了就不说了）

可以先让 \(n\) 个人分成两队比赛，然后对内再进行比赛，以此类推。

我们可以把比赛过程想象成一棵树。这里用 \(n=10\) 举例。

第一种情况可以这么分，那么第一场比赛就是 \([1,5]\) 和 \([6,10]\) 打。

接着，\([1,5]\) 和 \([6,10]\) 要在内部进行比赛。

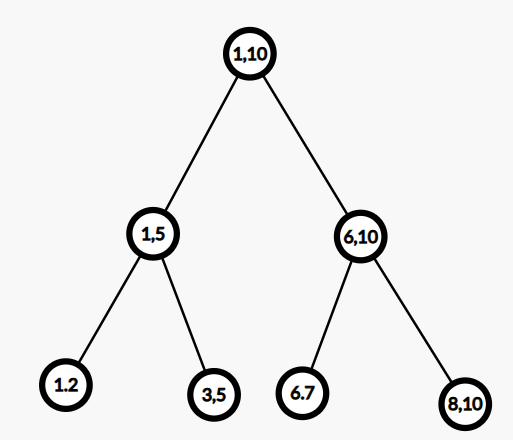
那么，很关键的一步，\([1,2]\) 和 \([3,5]\) 要在内部打，\([6,7]\) 和 \([8,10]\) 要在内部打。那，我们可以将 \([1,2]\) 和 \([6,7]\) 分到一队，\([3,5]\) 和 \([8,10]\) 分到另一队，这时候，虽然有些人会重复打，但是我们把两场比赛合并为了一场，简化了操作数量。

也就是说，他们实际上各打各的，互不干扰，只不过名义上是一支队伍罢了。

接着继续分，我就不过于详细的解释了。

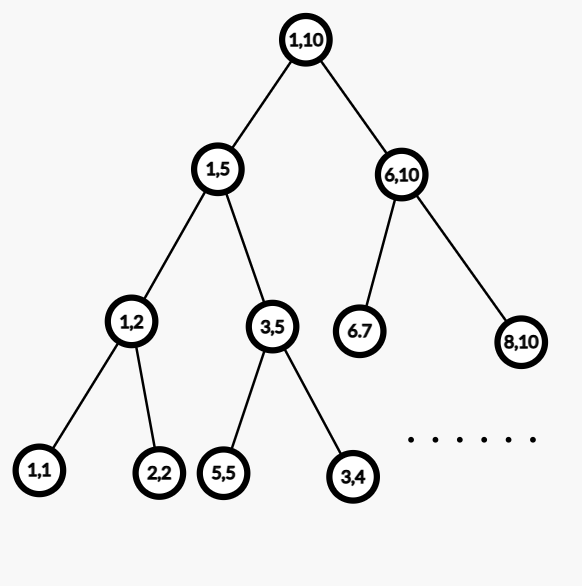
也就是说，我们可以构造一个长度为\(n\)的线段树，每次输出其叶子节点中的左节点即可。

在程序实现上，不需要真的构建出一个线段树，只需要维护其全部叶子节点即可。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
void FASTIN();
struct range
{
    int l,r;
    int root;//0 左节点 1 右节点
}f[1010],t[1010];
void play(int n)
{
    int ans=0,cnt=0;
    for(int i=1;i<=n;i++)
    {
        if(f[i].l==f[i].r) continue;
        int mid=(f[i].l+f[i].r)>>1;//分成左右两个部分，也就是内部继续对打
        cnt++;
        t[cnt].l=f[i].l,t[cnt].r=mid,t[cnt].root=0;
        cnt++;
        t[cnt].l=mid+1,t[cnt].r=f[i].r,t[cnt].root=1;
        ans+=mid-f[i].l+1;
    }
    for(int i=1;i<=cnt;i++) f[i]=t[i];cout<<endl;
    cout<<ans<<" ";
    bool flag=0;
    for(int i=1;i<=cnt;i++)
    {
        if(!f[i].root)
        {
            for(int j=f[i].l;j<=f[i].r;j++) cout<<j<<" ";
        }
        if(f[i].l!=f[i].r) flag=1;
    }
    cout<<endl;
    if(flag) play(cnt);
}
void run()
{
    int n,ans=0;
    cin>>n;
    while((1<<ans)<n) ans++;
    cout<<ans<<endl;
    f[1].l=1,f[1].r=n;
    play(1);
}
int main()
{
	freopen("input.txt","r",stdin);
	freopen("output.txt","w",stdout);
    FASTIN();
    int t=1;
    // cin>>t;
    while(t--) run();
    system("pause");
    return 0;
}
void FASTIN()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
}