CF128C Games with Rectangle

首先来明确一个点，假设我确定了四条竖着的边和四条横着的边：

接着如果向通过分别选择横竖不同的边，组成一个满足题目要求的嵌套矩形，那么选择方法一定是唯一的：

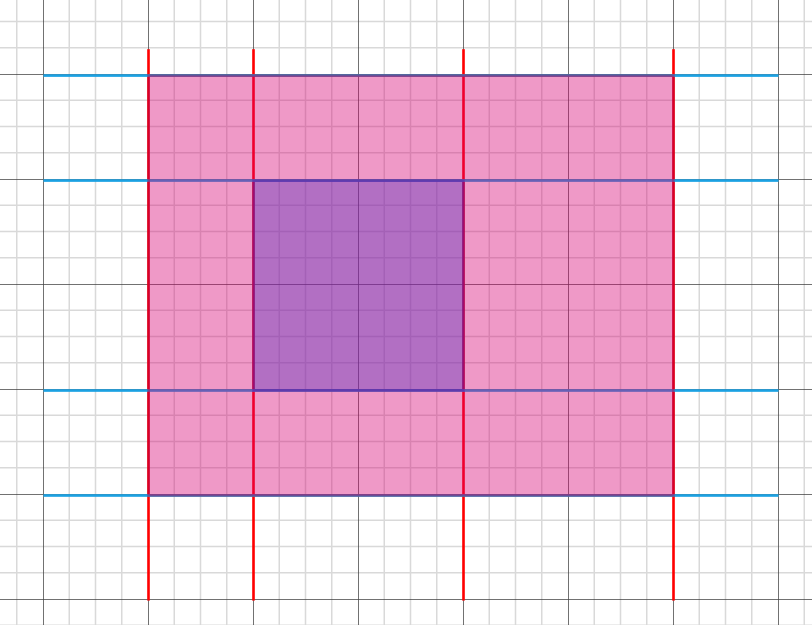
换句话说，只要我选择了四条边，就一定存在一组（两个）唯一的矩形能够满足题目所述条件

进一步推广，只要选择\(2k\)条边，就能够造出唯一的一组符合题目要求的矩形

那么最后，我们只需要从\(n,m\)条边中分别选出\(2k\)条边进行组合，计算共有多少种不同的情况，也就是\(C^{2k}_n\times C^{2k}_m\)

我使用了递推求\(C_n^m\)，也可以直接使用循环枚举（应该不会超时）

这里再解释一下递推式\(C_n^m=C_{n-1}^{m-1}+C^{m}_{n-1}\)

前半部分\(C_{n-1}^{m-1}\)计算的是如果当前第\(n\)个数选中，那么共有这么多种方式，后半部分\(C^{m}_{n-1}\)则是如果不选第\(n\)个数，有多少种情况，求和则是最终\(C^m_n\)的结果了

代码如下：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1e9+7;
int c[1010][1010];
int n,m,k;
signed main()
{
	cin>>n>>m>>k;
	if(2*k>n || 2*k>m)
	{
		cout<<0;
		return 0;
	}
	for(int i=1;i<=max(n,m);i++) c[i][0]=1;
	for(int i=1;i<=max(n,m);i++) c[i][max(n,m)]=1;
	for(int i=1;i<=max(n,m);i++)
	{
		for(int j=1;j<=max(n,m);j++)
		{
			c[i][j]=c[i-1][j-1]+c[i-1][j];
			c[i][j]%=mod;
		}
	}
	cout<<c[n][2*k]*c[m][2*k]%mod;
}