树和图的搜索

图  邻接矩阵   一般不用（浪费空间·）

邻接表     n个单链表

每个点只遍历一次

树和图的深度优先搜索

  

学习注意：认真！认真！认真！

邻接表  有几个点开几个单链表，表头也就是点数子指向

         自己可以指向的某个点，插入会进行更新

 

 

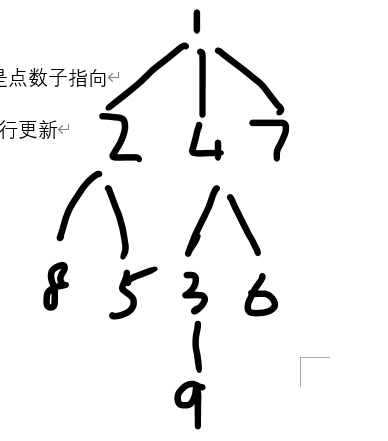
H[ 1 ]  == 1 ->2 ->4 ->7                                                          

 

H[ 2 ]  == 2 ->8 ->5

3 ->9

4 ->3 ->6

e[ N ] 存储点的数字，比如第一个  1  插入   2

然后就是e[ 0 ] = 2    为什么没1 呢? 因为h [1]  代表1 , h[ 1 ] = 0,指向 1（e[ 0 ] = 2），然后插入4，e[ 1 ] = 4 ,h[ 1 ]就等于1了，ne [ 1 ] = 0 (4的后继是2)。

单链表首先要初始化为-1， memset( h , -1 ,sizeof h )

头文件为：

  #include<string.h>//C语言

#include<cstring>//c++

 

例题：树的重心

   树的重心 ： 删除这个点后，剩余的连通块中的点的数量最大值最小。 就是枚举删除每一个点，连通块中的点的数量的最大值，然后每一个点的最大值相比较，找出其中的最小值。

 

 

 

树和图的广度优先搜索

 

长度为1，说明可以用宽搜

  每一次扩展一层，第一次发现这个点就是最短路径

      框架：

          Queen  <-  1  第一个点入队

           while(队列不空)

{

    t  < -  队头 （取对头）

   扩展t  的所以的邻点，也就是它能到的点x

If (x 未遍历)

{

 queen <- x

d [ x ] = d [ t ] + 1

}

}

如果已经遍历过这个点了，就不会再遍历，已经不是第一次，不是最短路径

代码：

 

 

 

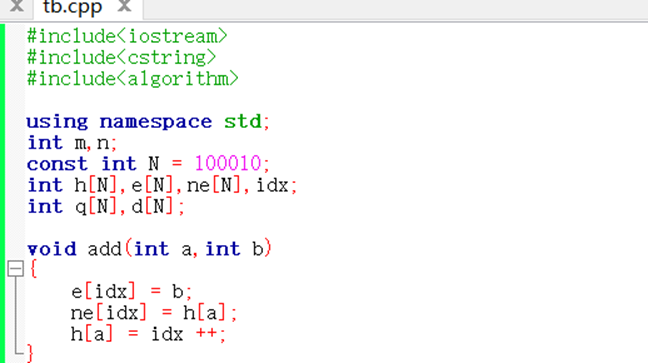
拓扑序列

  拓扑序列是对于有向图而言的，是其顶点的线性排序

  使得对于从顶点u到顶点v 的每个有向边u v ， u  在序列中都在v 之前

 

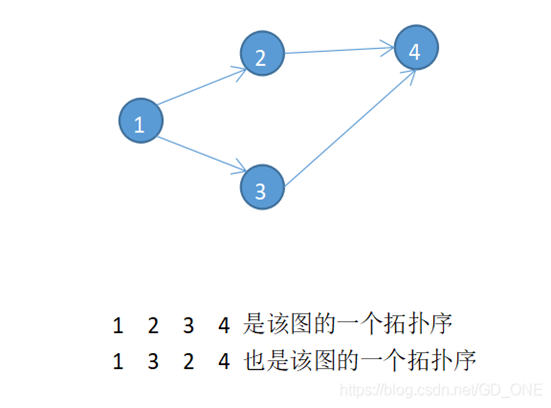
存在4条边：（1,3）（1,2）（2,4）（2,3）

图的拓扑序必须要满足以下两点：

1. 每个顶点只出现一次。
2. 对于图中的任何一条边，起点必须在终点之前。

题目：

 

入度：指向它的线的条数，入度为0的点都可以排在最前面，都是它指向别人，故先入队。

出度：从它出来的条数

框架：

     queen  <- 所有入度为0的点

     while(队列不空)

{

t  <-  对头

枚举t的所以出边  t -> j

删掉t -> j  d [ j ] --;

If  ( d [ j ] == 0 )

queen <- j

}

如果是一个环，不存在入度为0的点，就不会入队

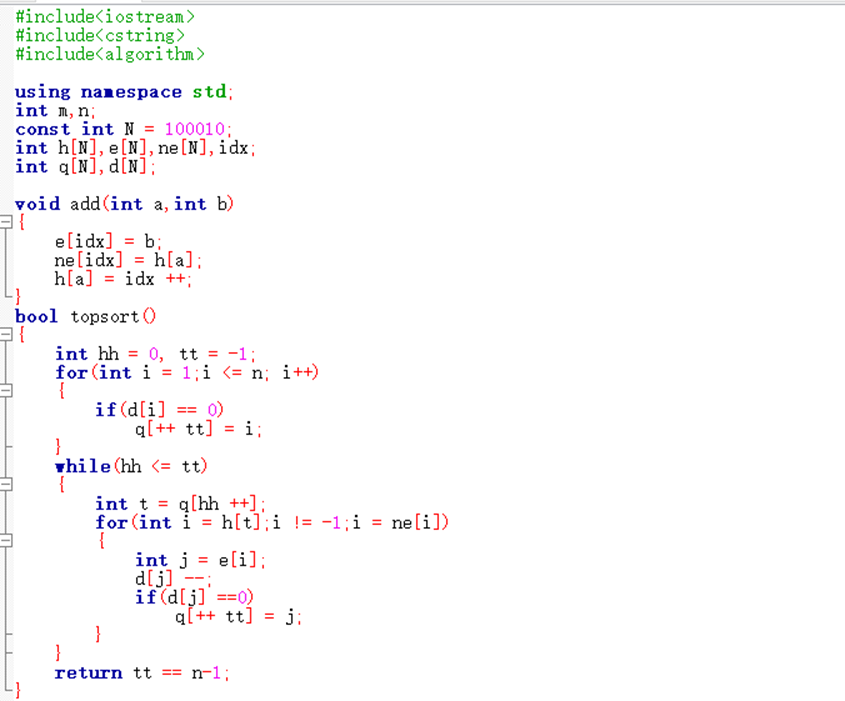
代码：