二分图

二分图

如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交子集 ，使得每一条边都分别连接两个集合中的顶点。如果存在这样的划分，则此图为一个二分图

一个二分图当且仅当没有奇数环

  如何判别是二分图

       染色法 dfs  O(n)

  求二分图的最大匹配

       匈牙利算法  O(mn),  实际运行时间一般远小于O(mn)

染色法

   二分图每一条边连接的两个点是不同集合的，所以我们给其中一个点染色，邻点染别的数字，就能确定每一个点染的数字，两个邻点染了相同的数，就说明不是二分图

见代码：

 

 

 

匈牙利算法

   解决的问题：二分图最大匹配问题，就是一个点只能匹配另一个点，最后的最大能匹配的数量。

比如：

 

如图：肯定是一个二分图，左1匹配由2，左2匹配右1，左3要匹配右2，但是右2已经匹配过了，匹配的是左1，我们需要看左1能不能匹配别的点，我们发现左1匹配右3，左3要匹配右2，左4匹配右4，右4组点匹配了，所有最大匹配数为4.

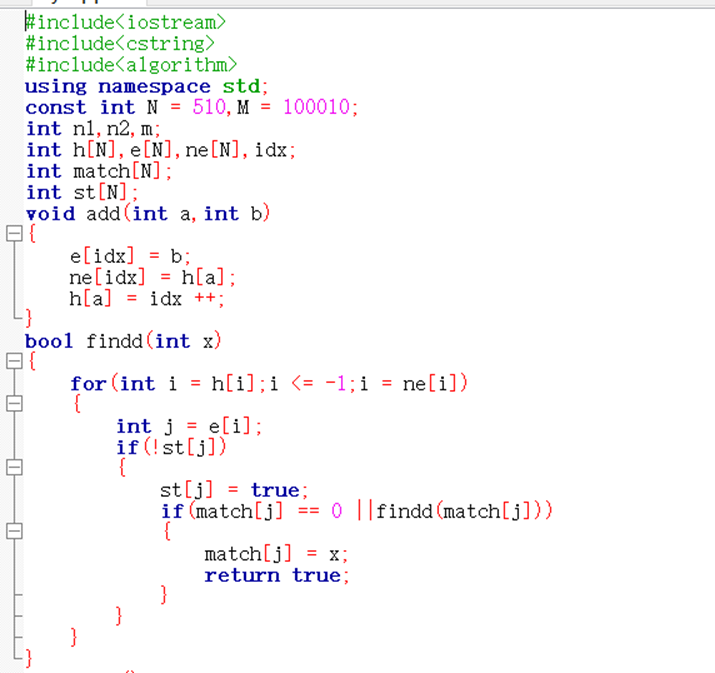
代码：