背包问题(0-1背包+完全背包)
0-1背包
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
重要的点在于:每种物品仅有一件,可以选择放/不放
子问题:f[i][v]表示前i件物品恰好放入一个 容量为v 的背包可以获得的最大价值。
状态转移方程(递推式):f[i][v]=max{f[i-1][v], f[i-1][v-c[i]]+w[i]};//考虑前i件物品放入这个子问题的时候,可以转化为前i-1件物品已经放好。那么如果放入第i件物品,那么问题转化为 前i-1件物品放入剩余容量为v-c[i]的背包里;如果不放入第i件物品,那么问题转化为 前i-1件物品放入剩余容量为v的背包里。
而如果放入第i件物品,那么当前价值就是f[i-1][v-c[i]]+w[i]。因此当前最大价值就是 放入&不放入 之间的最大值。

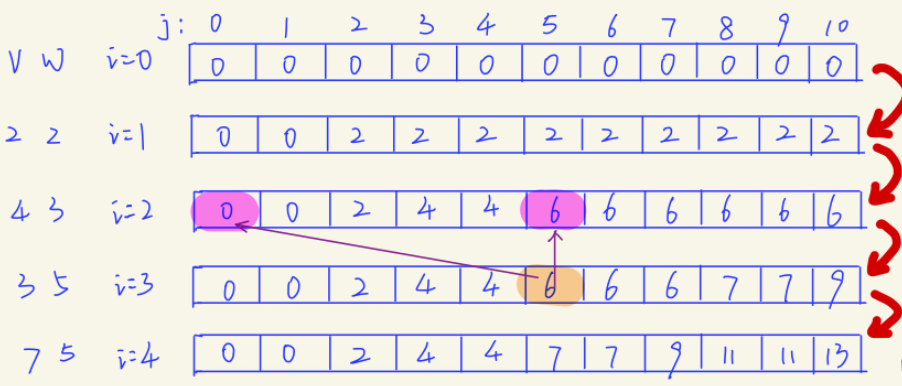
可以反向找到各种物品的选择:从dp[N][V]开始,如果dp[i][j]=dp[i-1][j],则当前第i件物品没有被选中,从dp[i-1][j]继续找;否则,则表示选中,从dp[i-1][j-w[i]]开始找
伪代码:
int[][] dp=new int[N][V+1]; //初始化第一行 //仅考虑容量为V的背包放第0个物品,不放物品,价值为0 for(int i=0;i<=V;i++){ dp[0][i]=0; } //初始化第一列
//容量为0的背包放物品,不放物品,价值为0
for(int i=0;i<=N;i++){
dp[i][0]=0;
} //根据状态转移方程,填充其他行和列 for(int i=1;i<N;i++){ for(int j=1;j<=V;j++){
//装不进去,当前剩余空间小于第i个物品的大小
if(w[i]>j){
dp[i][j]=dp[i-1][j];
}
//容量足够,可以放进去,比价值更大的方法
else{ dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]); } } } //最后的结果 dp[N-1][V]
如何优化呢?那么只能在空间复杂度上进行优化,只使用一维数组来存放结果
此时状态转移方程为:f[v]=max{f[v], f[v-c[i]]};//那么这个时候需要注意的是,在第二层循环中,需要使用从后往前计算,得到结果。即要用一维数组记忆化的时候,需要用到当前位置的值 和 该位置之前的值。因为如果我们需要计算f[4, 4]=max{f[3,4], f[3,1]}、f[4,3]=max{f[3,3], f[3,1]}、f[4,2]=max{f[3,2], f[3,1]}。
如果是转化为一维数组,因为需要保证max中的f[v]是f[i-1][v],前面的f[v]是f[i][v]。也就是当前这一层的d[j]还没有被更新过,所以当前的d[j]用到的是i-1层的结果。如果从前往后计算,那么下一次使用的d[j]是本层已经更新过的,会覆盖掉i-1层的结果。
//解释
由于知道dp[i-1,1...j]就可以得到dp[i,j],下一层只需要根据上一层结果就可以推出答案。
对于dp[j]=max{dp[j], dp[j-w[i]]+v[i]}而言,dp[j-w[i]]相当于二维的dp[i-1][j-w[i]],dp[j]是由前面的dp(1...j)推出来的。
因此比如从i=3推i=4,此时一维数组存放{0,0,2,4,4,6,6,6,7,7,9},这是i=3时所有子问题的解。如果从前往后推,那么计算i=4时,
dp[0]=0, dp[1]=0, ... , (前面这几项都放不进 w[i]=5的物品)dp[5]=max{dp[5], dp[5-5]+7}=7, dp[6]=max{dp[6], dp[6-5]+7}=7, dp[7]=max{dp[7], dp[7-5]+7}=9.....这里会更新dp[5]、dp[6]...的值,那么后续计算的时候 就没办法用到 上一轮循环时的 dp[5]、dp[6]....了(即 因为当前值 是由上一轮循环推出来的,如果从前往后,前一次循环保存下来的值 可能会被修改)就是我当前更新要用到这个值,但是这个值 在从前往后更新时,已经被修改了,那么我用到的就是错误的值了。
初始化的话:(初始化 实际上是 在没有任何物品可以放入背包时 的合法状态)
如果问法是“恰好装满”的最优解,那么除了dp[0]初始化为0,其他都应该设置为 负无穷大。这样能保证最终的dp[V]为恰好装满背包时的最优解。此时,只有容量为0的背包 可以在 什么都不装且价值为0时被“恰好装满”,因为如dp[3]则表示,背包容量为3时,恰好装满的价值,此时没有合法的解,因此属于未定义状态,设为无穷大。
如果问法是“可以不装满”的最优解,那么所有的都应初始化为0,因为“什么都不装”时,0就是合法解。
伪代码:
int[] dp=new int[V+1]; //初始化第一行 //仅考虑容量为V的背包放第0个物品,不放物品,价值为0 for(int i=0;i<=V;i++){ dp[i]=w[0]<=i?v[0]:0; } //根据状态转移方程,填充其他行和列 for(int i=1;i<N;i++){ for(int j=V;j>=w[i];j--){ dp[j]=Math.max(dp[j],dp[j-w[i]]+v[i]); } } //最后的结果 dp[V]
例题:给定一个仅包含正整数的非空数组,确定该数组是否可以分成两部分,要求两部分的和相等
思路:即给定N个元素组成的数组arr,数组元素的和为sum。转换成背包问题,每个物品的重量和价值为arr[i],两部分和相等,即背包的限重为sum/2.
if(nums==null || nums.length==0){ return true; } int sum=0; for(int num : nums){ sum+=num; } //如果sum不可以平分,那么就不可分为两块 if(sum%2!=0){ return false; } sum/=2; //定义 boolean[] dp=new boolean[sum+1]; //初始化
dp[0]=true; for(int i=1; i<nums.length; i++){
//为什么要从后往前更新dp,因为每个位置 依赖于 前面一个位置 加上 nums[i]。如果从前往后更新的话,
那么dp[i-2]会影响dp[i-1],然后dp[i-1]会影响dp[i],即同样的一个nums[i]被反复使用了多次。
for(int j=sum; j>=nums[i]; j--){ dp[j]=dp[j] || dp[j-nums[i]]; } } //输出 dp[sum]
例题扩展:传入数组的大小+一个int型数组,返回该数组能否分成两组, 使得两组中各元素加起来的和相等。
并且,所有5的倍数必须在其中一个组中,所有3的倍数在另一个组中(不包括5的倍数),能满足以上条件,返回true;不满足时返回false。
public static void main(String[] args) { Scanner scanner = new Scanner(System.in); while(scanner.hasNextInt()) { int count = scanner.nextInt(); int sum3 = 0; int sum5 = 0; int sumTemp = 0; List<Integer> otherNums = new ArrayList<Integer>(); for(int i=0; i<count; i++) { int num = scanner.nextInt(); //因为所有3的倍数组中不包括5的倍数,因此先处理5的倍数。如15应该是在5的倍数组里 if (num%5==0) { sum5+=num; } else if (num%3==0) { sum3+=num; } else { otherNums.add(num); sumTemp+=num; } } //如果刚好都是3和5的倍数,那么不需要进行接下来的步骤 if (otherNums.size()==0) { if (sum3==sum5) { System.out.println("true"); } else { System.out.println("false"); } } //接下来问题转化为,将剩余不是3和5的倍数的数,均分到两个组里。使得 //3的倍数组之和+组A=5的倍数组之和+组B -->(3的倍数组之和-5的倍数组之和)+组A=组B-->可以把两组之差当成一个值 else { int minus = sum3-sum5; //把两组之差当成一个值 if (minus!=0) { otherNums.add(minus); sumTemp+=minus; } //如果不能均分,那么返回false if (sumTemp%2!=0) { System.out.println("false"); } else if (canDivided(otherNums, otherNums.size(), sumTemp/2)) { System.out.println("true"); } else { System.out.println("false"); } } } } //是否可以将链表中的数分为两组,每组的和为总和的1/2。
//这里用的是二进制枚举,二进制的每一个01位可以当成这个数字加不加进去
private static boolean canDivided(List<Integer> otherNums, int size, int sum) { // TODO Auto-generated method stub int count = (int) Math.pow(2, otherNums.size()); for(int i=0; i<count; i++) { int curSum = 0; //转化成2进制输出,当这一位为1时,加上。即有这么多种可能,每一位是否加入 String str = Integer.toBinaryString(i); for (int j = 0; j < str.length(); j++) { char yesOrNo = str.charAt(j); if (yesOrNo=='1') { curSum+=otherNums.get(j); } else { continue; } } if (curSum == sum) { return true; } } return false; }
//上一个函数还可以用01背包的方法来做。
private static boolean canDivided(List<Integer> otherNums, int size, int sum) {
boolean[] dp = new boolean[sum+1];
dp[0]=true;
//System.out.println("otherNums.size()="+otherNums.size());
for(int i=1; i<otherNums.size(); i++) {
System.out.println("otherNums.get(i)="+otherNums.get(i));
for(int j=sum; j>=otherNums.get(i); j--) {
dp[j]=dp[j] || dp[j-otherNums.get(i)];
}
}
return dp[sum];
}
完全背包
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
重要的区别在于完全背包是 每种无限件
状态转移方程:f[i][j]=Math.max(f[i-1][j-k*c[i]]+k*w[i]),0<=k*c[i]<=j;//根据第i件物品放多少件,即前i-1件物品中 选择 若干件 放入剩余的空间上,使得最大。(f[i][j]表示 前i种物品 放入一个容量为j的背包种获得 最大价值)
//递归和动态规划的区别:动态规划多使用了一个二维数组来存储中间的解
代码:
int[][] dp=new int[N][V+1]; //初始化第一行 //仅考虑容量为V的背包放第0个物品,不放物品,价值为0 for(int i=0;i<=V;i++){ dp[0][i]=0; } //初始化第一列 //容量为0的背包放物品,不放物品,价值为0 for(int i=0;i<=N;i++){ dp[i][0]=0; } //根据状态转移方程,填充其他行和列 for(int i=1;i<N;i++){ for(int j=1;j<=V;j++){ //装不进去,当前剩余空间小于第i个物品的大小 if(w[i]>j){ dp[i][j]=dp[i-1][j]; } //容量足够,可以放进去,比价值更大的方法。取k个物品i,再k种选择 选出 最优解 else{ for(int k=0; k*w[i]<=j; k++){ dp[i][j]=Math.max(dp[i-1][j], dp[i-1][j-w[i]*k])+v[i]*k; } } } } //最后的结果 dp[N-1][V]
同样使用一维数组 来优化 空间复杂度
dp[i]=Math.max(dp[i], dp[i-w[i]]+v[i])
int[] dp=new int[V+1]; //初始化第一行 //仅考虑容量为V的背包放第0个物品,不放物品,价值为0 for(int i=0;i<=V;i++){ dp[i]=0; } //根据状态转移方程,填充其他行和列 for(int i=1;i<N;i++){ for(int j=w[i];j<=V;j++){ dp[j]=Math.max(dp[j],dp[j-w[i]]+v[i]); } } //最后的结果 dp[V]
(示意图源于网络,侵删)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号