随机过程的学习之路(一、概率论基础)

一、基础回顾

1.条件概率：  

   假设两个事件 A, B ，条件概率P(A|B)= P(AB)/P(B)   进而可以得到乘积公式：  P(AB)=P(A|B)P(B)

  其中需要搞清楚，P(A|B)的意思是 在 B事件已经发生的状态下，A发生的概率；而 P(AB)的意思是事件A和事件B同时发生的概率。

2.全概率公式：   （参考https://www.zhihu.com/search?q=%E5%85%A8%E6%A6%82%E7%8E%87%E5%85%AC%E5%BC%8F&utm_content=search_suggestion&type=content）

   

 

    

 

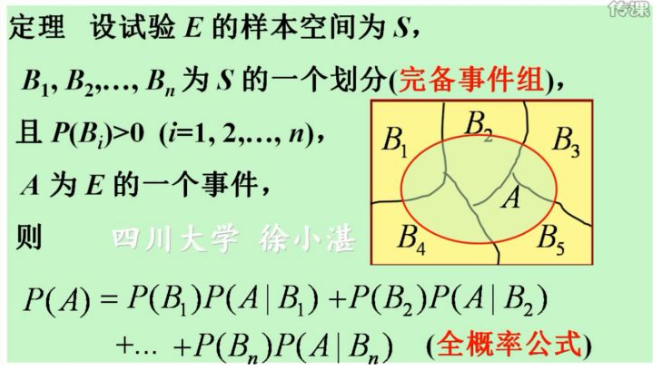
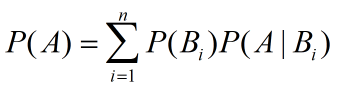
     推导如下：

 

 

 其意义是   将复杂的事件A划分成较简单的事件AB_i ,再结合加法和乘法公式计算出A的概率

事件A由多个原因B_i引起，故A发生的概率是全部原因引起A发生的概率总和，叫做全概率公式。

例题：

 3.贝叶斯公式：

 

 由条件概率出发，分子通过一步条件概率变形，分母通过全概率公式变形。重点：不必分子分母同时变形，只变其中之一也行。

 

 

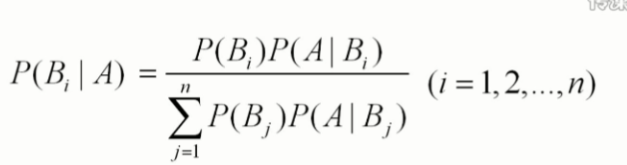
其意义是 在事件A已经发生的条件下，贝叶斯公式可以用来寻找导致A发生的各种原因B_i的概率。

 

 

总结来说：全概率公式是 由原因去推结果的概率

                 贝叶斯公式则是 由结果来推原因的概率

需要注意的是  在贝叶斯公式的题目之中，往往会得到一个需要使用全概率公式解决的分母，例3可以显然看到。