BUAA-OO-第一单元总结
BUAA-OO-第一单元总结
一、需求分析
1.0 形式化表述
- 表达式 → 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
- 项 → [加减 空白项] 因子 | 项 空白项 ' * ' 空白项 因子
- 因子 → 变量因子 | 常数因子 | 表达式因子
- 变量因子 → 幂函数 | 三角函数 | 自定义函数调用 | 求和函数
- 常数因子 → 带符号的整数
- 表达式因子 → ' ( ' 表达式 ' ) ' [空白项 指数]
- 幂函数 → (函数自变量 | ' i ' ) [空白项 指数]
- 三角函数 → 'sin' 空白项 ' ( ' 空白项 因子 空白项 ' ) ' [空白项 指数] | 'cos' 空白项 ' ( ' 空白项 因子 空白项 ' ) ' [空白项 指数]
- 指数 → '' 空白项 [' + '] 允许前导零的整数**
- 带符号的整数 → [加减] 允许前导零的整数
- 允许前导零的整数 → (0|1|2|…|9){0|1|2|…|9}
- 空白项 → {空白字符}
- 空白字符 → ``(空格) |
\t - 加减 → ' + ' | ' - '
- 自定义函数定义 → 自定义函数名 空白项 ' ( ' 空白项 函数自变量 空白项 [' , ' 空白项 函数自变量 空白项 [' , ' 空白项 函数自变量 空白项]] ' ) ' 空白项 ' = ' 空白项 函数表达式
- 函数自变量 → ' x ' | ' y ' | ' z '
- 自定义函数调用 → 自定义函数名 空白项 ' ( ' 空白项 因子 空白项 [',' 空白项 因子 空白项 [',' 空白项 因子 空白项]] ' ) '
- 自定义函数名 → ' f ' | ' g ' | ' h '
- 求和函数 → 'sum' ' ( ' 空白项 ' i ' 空白项' , ' 空白项 常数因子 空白项 ' , ' 空白项 常数因子 空白项 ' , ' 空白项 求和表达式 空白项 ' ) '
- 函数表达式 → 表达式
- 求和表达式 → 因子
1.1 hw1
读入一个包含加、减、乘、乘方以及括号(其中括号的深度至多为 1 层)的单变量表达式,输出恒等变形展开所有括号后的表达式。(只涉及幂函数和常数,重点是建立起表达式,项,因子三个层次)
1.2 hw2
读入一系列自定义函数的定义以及一个包含简单幂函数、简单三角函数、简单自定义函数调用以及求和函数的表达式,输出恒等变形展开所有括号后的表达式。(相比第一次作业增加了求和因子,三角函数因子,自定义函数因子)
1.3 hw3
第三次作业相比第二次作业需求没有太大变化,仅仅增加了三角函数组合因子,函数调用组合因子,即三角函数和函数实参可嵌套复杂因子。
二、方案实现与问题分析
2.1 hw1实现方案
利用课程组训练代码提供的提示,建立表达式,项,因子三个层次的概念,理解到表达式的解析可以是一种不断递归下降的过程,从表达式层面到项层面,从项层面到因子层面,从因子层面可能回到表达式层面,经有限次递归总能够到达最简单的因子层面,这是贯穿三次作业的解题思想,也使我们能够比较清晰的设计对象,明白各个对象间的关系。第一次设计方案比较简单粗暴,建立表达式,项,因子三个类递归建立对象调用方法,然后一个工具类帮助解析字符串,一个统一表达形式类用于递归到最底层后返回。
2.2 hw2,hw3实现方案
第二次和第三次的设计架构是没有变动的,只是在一些具体的字符串解析方法上有些变化。依旧是主体表达式,项,因子三个类,然后因子层面由于有各种不同的因子,分别建立了对应的常数类,幂函数类,三角函数类,求和函数类,自定义函数类,表达式因子类,最后有个统一表达形式的类,由于需要对表达式预解析一下和存取输入的自定义函数,留有一个工具类。
2.3问题分析
三次作业下来,过程中遇到了很多问题,很多时候可能就面向过程编程,硬着头皮上了。即使到了最后,自己的架构依旧是不优雅,层次关系过于简单,一些类和方法复杂度过高,类与类之间配合不够,没有很好的抽象设计,最大的一个问题或许是少了计算的层次,没有乘类,加减类。总的来说,因子层面的抽象设计不够,缺少计算层次。了解到他人的设计架构,并结合题目的形式化描述,可以发现出现计算这个层面是很自然的,递归下降的过程就是通过操作符为标志来拆解出项,因子对象的。对于因子层面,不同因子的处理方法是类似的,而我没有建立起因子和具体因子之间的关系,一方面导致结构不优雅,另一方面没有提高代码复用度,而如何抽象出因子层面的共性与个性正是体现个人设计与面向对象思想魅力的地方。
遇到的另一个问题是如何设计出统一形式存储类用于返回。由于因子层次可以递归到表达式层次,所以我们需要一种能够兼容表达式,项,因子三个层面的返回形式。从题目其实就能够知道,表达式本身就是兼容三个层次的,项,因子我们也可以把其当作表达式处理,这样也为复杂因子的嵌套提供了解决方法。了解了他人的一些存储方式后,我发现自己的设计分解的依旧不够彻底,分解到最底层并通用的存储形式是项层面,而我直接建立表达式层面的存储形式,把合并因子和合并同类项的方法都糅合在这个类里面了。
其他的是一些琐碎的问题,例如合并因子和合并同类项,采取适当的容器可以带来极大的便利。如用HashMap<base,expo>来存储因子可以实现因子合并,方便相同base的因子的指数相加。用HashMap<term,coe>可以方便同类项系数的加减。还由一些字符串替换处理的问题,如sum函数中有sin,那么替换i的时候需要注意到sin中的i;自定义函数中,形参x,y,z的替换需要注意到替换x时,可能替换了实参的x;然后就是不论是sum函数还是自定义函数,替换时需要我们对原始表达进行一定的解析化简,然后我们带着括号替换,这样表达式前后的语义一般是一致的。另一方面是数据的鲁棒性问题,注意到数据范围的限制,如系数需要BigInteger类型,sum中的s和t也需要BigInteger类型。最后,解析字符串时,刚开始我是采用的正则匹配,然后发现很容易就出现问题,大概我学艺不精,思考不够周到,第三次作业我基本上都替换成遍历的方式去解析字符串了。
三、程序结构分析
3.1 hw1程序结构
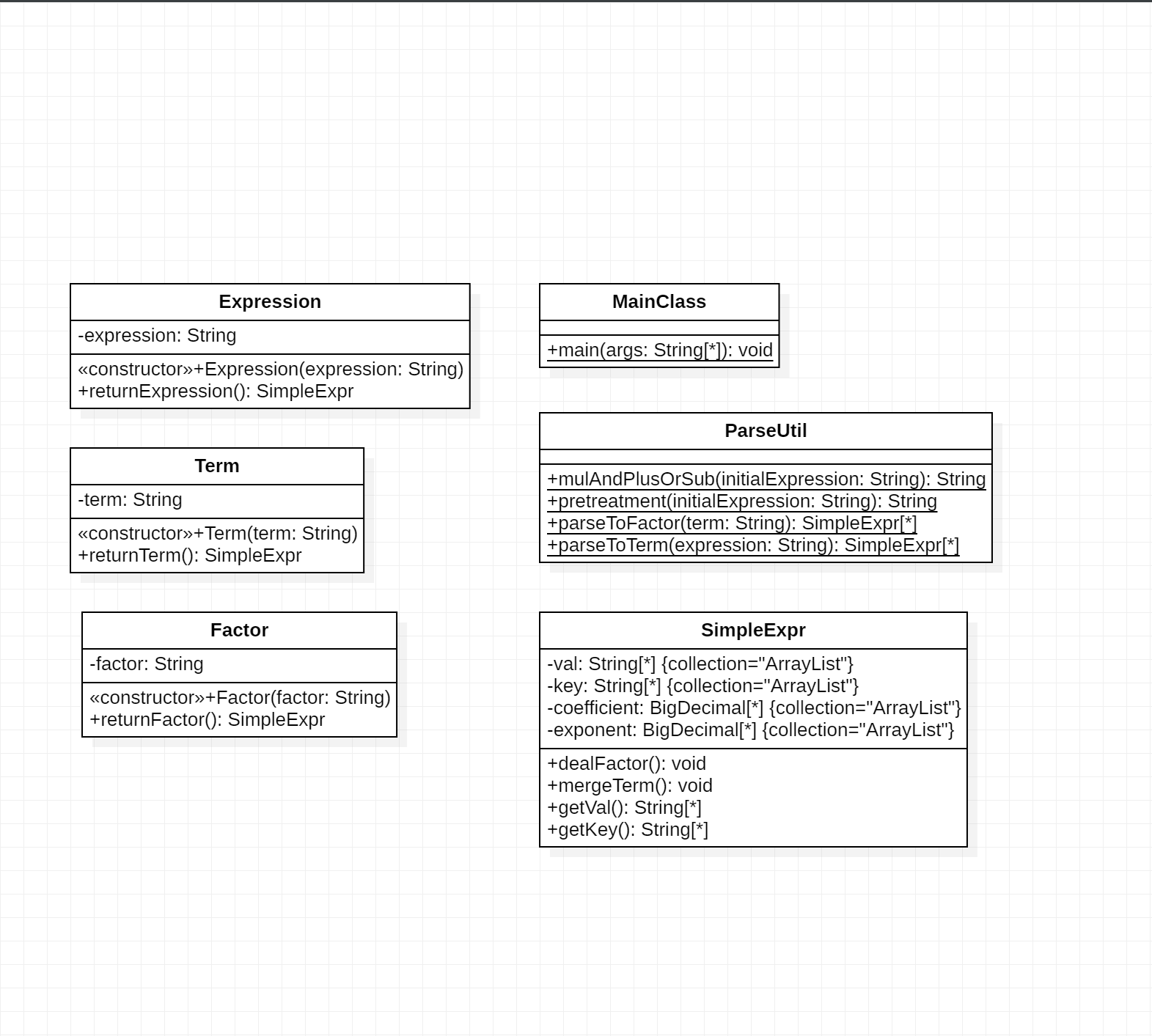
第一次作业中,Expression,Term,Factor类都只有个string属性和一个返回统一表达形式的方法;而工具类ParseUtil中聚集了过多的静
态方法,包括预处理方法,解析项,因子的方法;而统一表达形式的SimpleExpr类中,val存储了未处理的项,key存储了每一项的符号,coe是处理后的系数,expo是处理后的指数,dealFactor是因子合并方法,mergeTerm是合并同类项的方法。
3.2 hw2,hw3程序结构
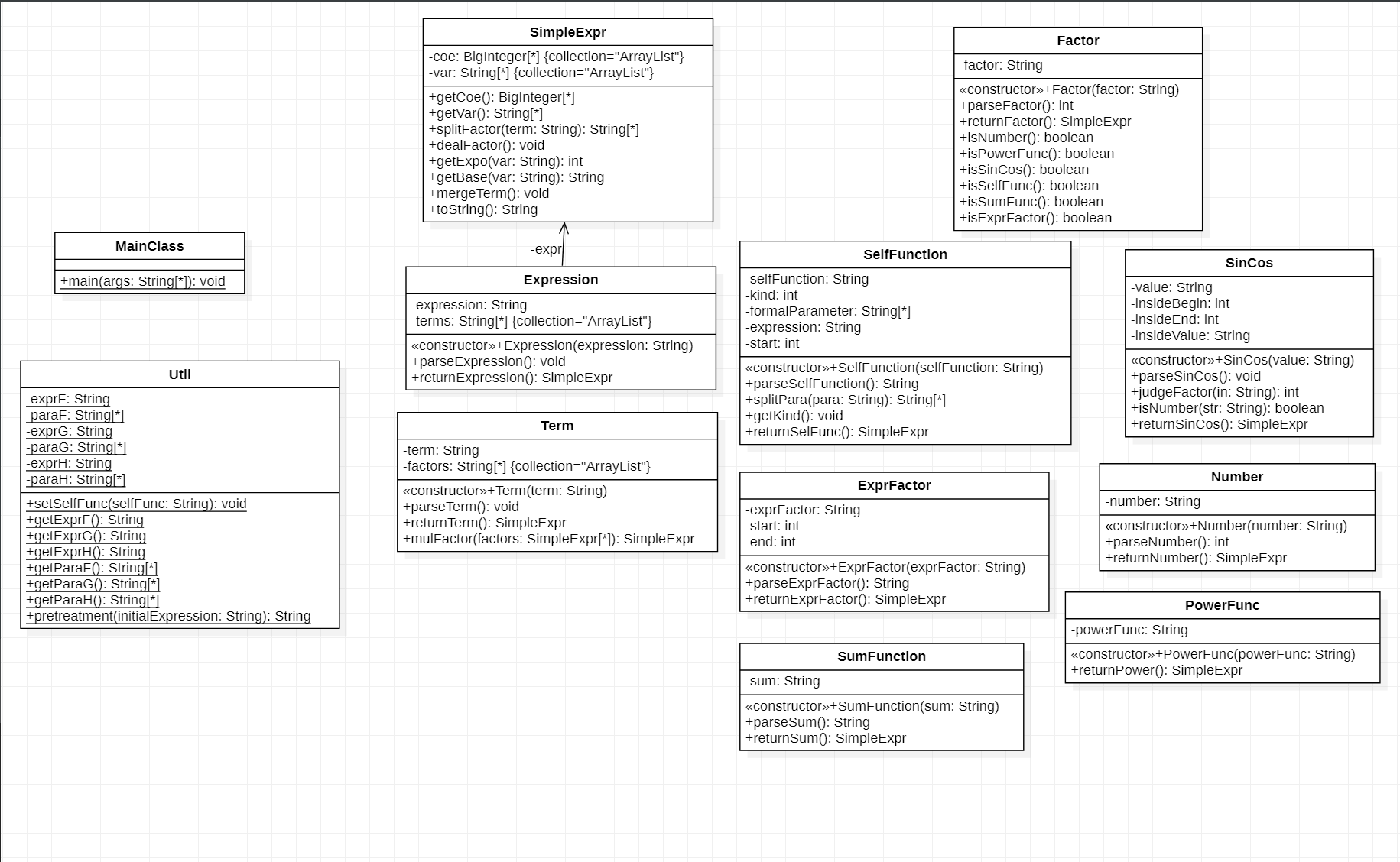
第二次和第三次作业中,Expression,Term,Factor类主要是解析各自的string属性,然后生成相应下级层次并返回统一存储形式,如Expression解析自己获得一组Term类的string,生成Term并调用Term的returnTerm方法返回SimpleExpr。乘号计算是默认在Term类中进行,所以Term类有个mulFactor方法来计算因子相乘。Factor类更像一个因子识别器,识别因子并生成相应因子,然后在相应因子类中进行解析并返回SimpleExpr。六种具体的因子中,采用不同方式进行解析各自的string并返回SimpleExpr。加减类的计算我直接当作系数的一部分扔给因子了,导致的结果是每次解析因子我都需要判断下正负号。Util工具类主要是用来存储输入的自定义函数以及对输入的表达式进行一些简单的预处理。
3.3 hw1代码度量分析
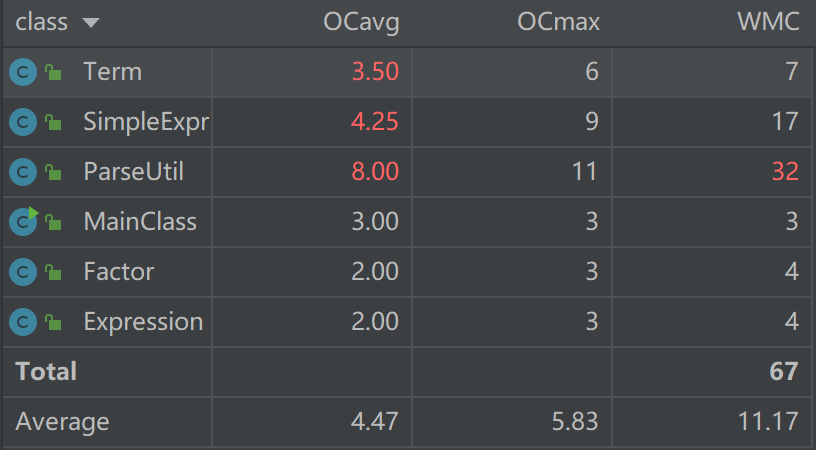
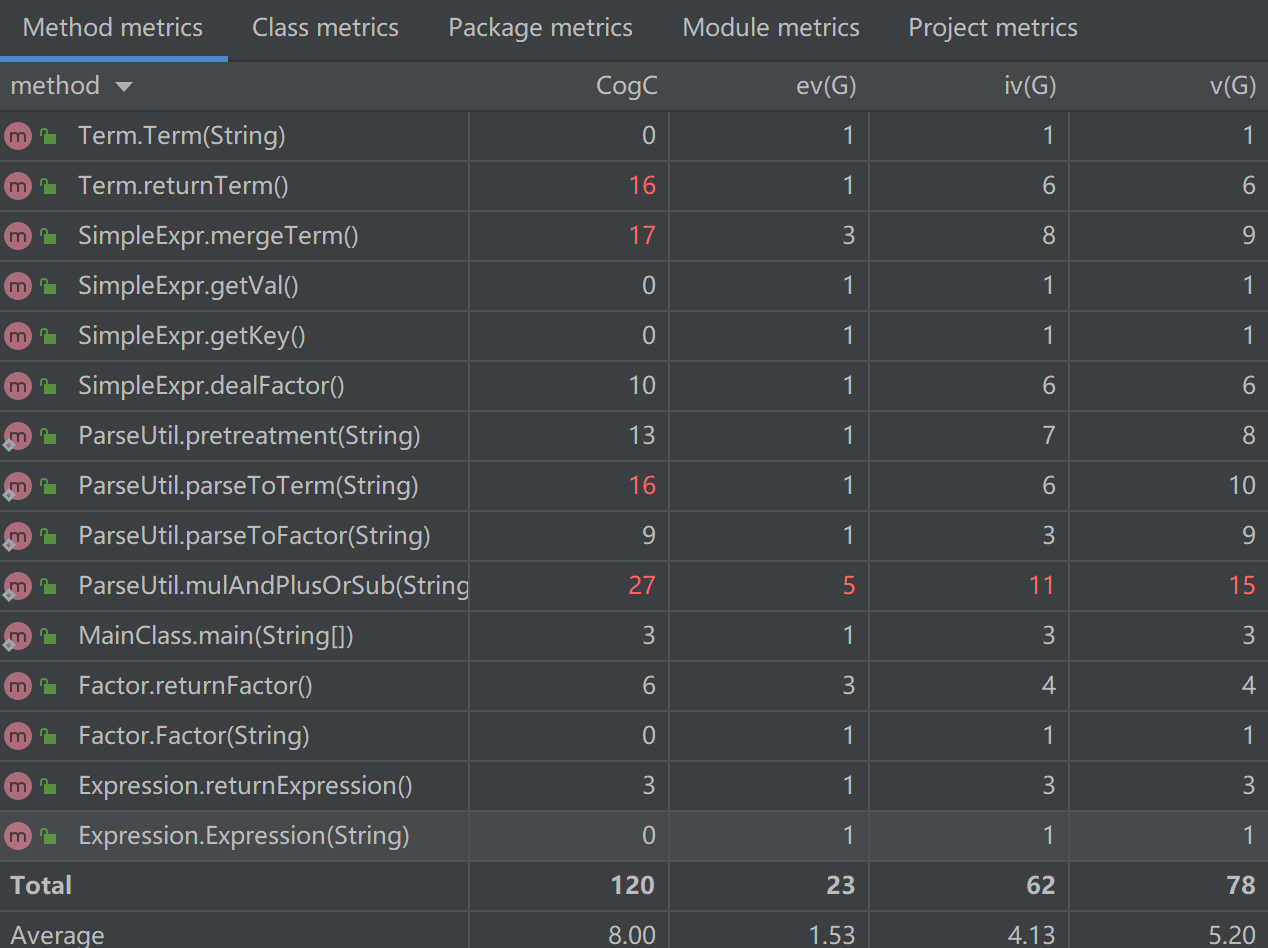
Term类中主要是returnTerm方法中还集成了因子相乘的计算,导致平均操作复杂度较高;SimpleExpr中有合并同类项和合并因子方法,平均操作复杂度较高。而ParseUtil类中有着太多的解析字符串的方法,加上一些地方操作比较笨拙,导致平均操作复杂度和加权方法复杂度爆表。从方法的复杂度度量可以看到ParseUtil类的一些预处理方法路径过多,认知复杂度很高,预处理过于复杂,圈复杂度过高。总的来说,第一次作业比较面向过程编程,主要操作方法过于集中,导致复杂度较高。
3.4 hw2,hw3代码度量分析
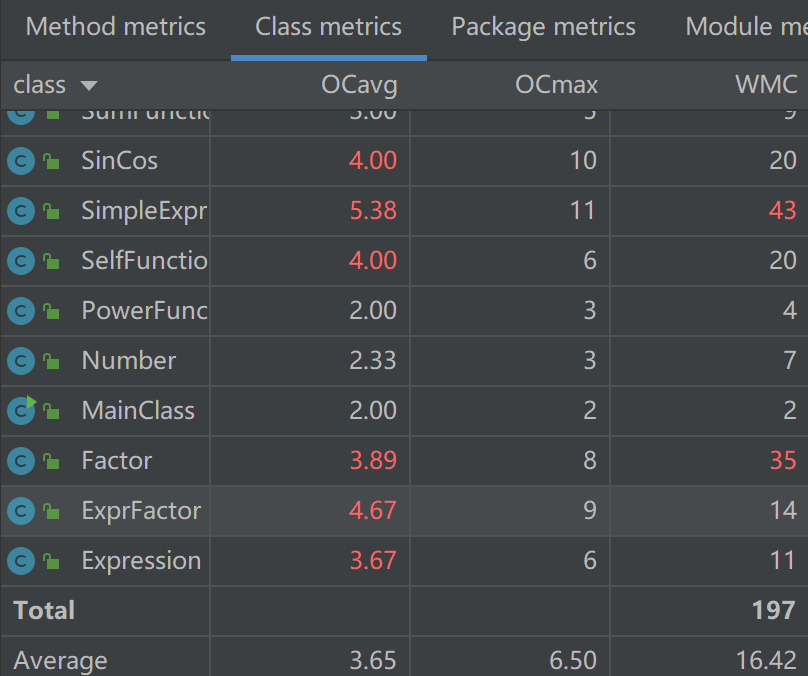
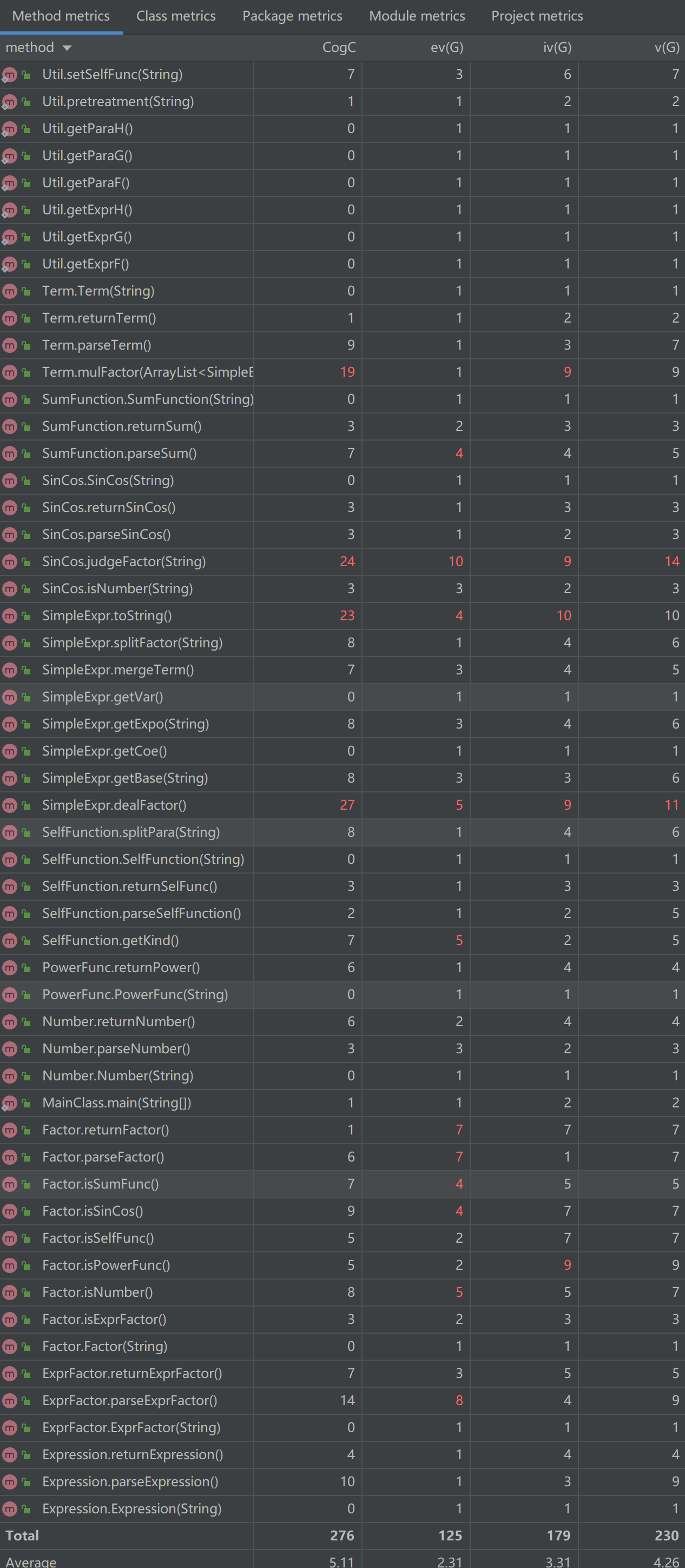
Term,Expression类主要是调用了合并因子和合并同类项的方法导致OCavg较高,SimpleExpr中有着合并因子和合并同类项的方法,导致OCavg和WMC较高。一些ev(G)和iv(G)较高的方法主要是判断路径过多。由于并没有在因子层面进行很好的抽象,加之把正负号扔给了因子层面处理,导致各类因子的解析字符串方法判断路径过多,复用性太差,做了很多类似相近的工作。
四、bug分析
hw1中遇到的bug主要是预处理时进行*和-号相连的处理少考虑了一种情况。hw2中还是字符串处理替换的bug,一个是sum中sin的替换,一个是遍历字符串的循环找到对应条件后忘记了break。hw3中的bug主要是sum函数的s,t的数据范围设成了int。
在互测中,我的hack方案主要是利用自己在编程过程中遇到的一些问题去hack,考虑一些数据的鲁棒性,字符串处理过程中可能容易出现问题的地方。
五、架构设计体验
5.1 hw1
进行hw1设计时确实非常困难,设计出来的架构也不理想,第二周就重构了一次。刚开始我脑海中构思如何递归下降解析字符串时是先从最底层开始的,默认我得到的项,表达式都是很标准的形式,然后把那些多个操作符相连的情况交给预处理去解决。解析到最底层,由于因子包含表达式因子,开始一直不知道怎么返回,后面想通我需要一个统一的存储形式才贯通整个解析返回过程。
5.2 hw2,hw3
hw2和hw3其实整个思考的过程就比较通畅了,无非就是采用递归下降的方法去解析,解析到最底层返回常数因子,幂函数因子,三角函数因子中的一种。 至于组合因子的处理,其实从递归下降的处理过程我们就可以发现,根本就不畏惧这种情况,无非是需要继续递归而已,由于输入符合形式化的表述,经过有限次递归我们总能找到最底层的因子。
六、心得体会
首先最大的收获是学习了递归下降的方法,学会分析问题,建立层次。把层次建立后,我们才可能去设计对象,考虑对象间的共性和个性以便建立抽象层次。对于面向对象的思想更加深刻了,对象是属性和行为的集合,各个对象处理自己的事务,通过互相配合来解决问题。为了减少bug,在设计对象时,要减少方法的复杂度和耦合,使对象的状态改变原因清晰明了。
通过研讨课,讨论区,互测以及各种各样的途径,也了解了很多优秀的设计架构,看到别人处理问题的不同方法拓展了我思考问题的角度,也经常让我觉得自己的设计着实丑陋。另一方面,也帮助我避免了许多坑点。
学会了去考虑程序可能出现的bug,在分析问题的时候考虑数据输入的鲁棒性,方法的复杂度往往决定bug出现的可能性。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号