浅谈卡特兰数
什么叫卡特兰数
卡特兰数是组合数学中的一个分支,主要用于求解在一定的条件下满足条件的方案数,在此,我们将通过一些题目来帮助你理解卡特兰数。
一些基本的题型
括号问题
题面:比如有 n 个左括号,有 n 个右括号,求解有多少个合法的方案能使括号两两配对?
或许大多数人在看到这类括号的问题,都会有一种无力感,无奈之下,只能择打暴力,但肯定是不优的,毕竟实在是太慢了。
其实,这是卡特兰数的经典例题,在了解它之前,我们先了解一下 young 表 ,所谓 young表 ,就是将1至2n个数填入一个2*n的方格表中,使得每一行自左而右,每一列自上而下都是严格递增的。
当n=3时,有 5 种不同的标准 young表。

那我们如果将第一行上的每个数表示为"("的位置,第二行上每个数表示为")"的位置,那么每一个young表 都能对应一个匹配的括号串。
比如说以下这个表:
1 3 4
2 5 6
得出:
1 2 3 4 5 6
( ) ( ( ) )毫无疑问,这是合法的。那么一个长度为2*3的括号串的总合法方案的数目为5种。
那为什么他是对的呢?
我们在第一行填入的数一定是小于自己下面的数字的,那么最后一个数字 2*n肯定是在最后一行的最后一位上,就这样地,我们能保证每个"("都有一个在右边的")",而不至于出现类似于“())(”的情况,而正是如此,也不会出现交错的现象,因为数目固定为偶数。
(不用着急了解卡特兰数,我们先看完接下来几道题)
排队问题
题面:给定2*n个人,排成两排,每排自左往右必须是从高到矮排列,并且第二排的每个人都比他前面的第一排的人高,问有多少中排列方式?
毫无疑问,这就是一道标准 young表 的问题,你完全可以从标准 young表 的角度审视这道题。
出入栈问题
假设入栈顺序为1......n,所有可能的出栈数目为多少。
说白了就是有多少中出入栈的方案数,我们尝试枚举一个小一点的数。
考虑当 n=3时,有一共5种方案。

我们想想我们经常用栈处理什么问题?不错,是 括号问题,因为他有一种先进后出的特性,那么我们这里完全可以转换为括号匹配问题来做。
最经典的就是列车调度问题。
Dyck words问题
所谓长为2n的Dyck words指的是由n个0和n个1组成的串,要求从第一个字符开始的任意连续前缀都满足0的个数不少于1的个数。
在遇到这个题的时候,一开始我也是一脸懵逼的,但是,如果我们仔细想想,我们可以发现这就是个括号匹配问题,假如我们将0看做“(”,把1看做“)”,那么我们就可以得到一个括号串,我们都知道,如果一个括号串合法,那么前x个括号里面“)”的个数肯定不会大于“(”的个数 ,因为那样就会直接不合法。就这样的,我们成功地将其转换为括号问题。
我们来看个例子:有2n个人排队购票,票价为50软妹币,其中的n个人手中有面值刚好为50的软妹币,另外n个人有100的,收银台一开始没有任何钞票,求有多少种合法的方案使每个人都能在不发生无法找钱的尴尬处境下顺利地买到票。
毫无疑问,我们可以将其转换为一个Dyck words问题,将那些手握50元软妹币的人视作0,其余的视作1,然后用卡特兰数就可以了。
群峰问题
题面:目前你能画 n 条斜向上的线条,也能画 n 条斜向下的线条,每条线条的长度都是相等且固定的,问你能画出多少种群峰?
我们考虑事先枚举,当n=3时,我们可以画出5种群峰:
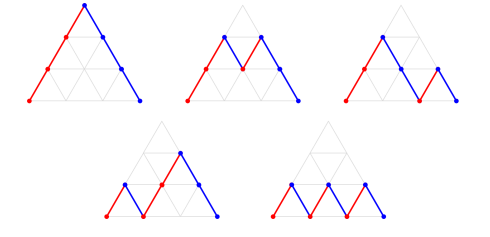
怎么做呢?
我们能发现,只要这两种线的长度相等且数目相等,那么我们一定能在最后一次回到高度为0的位置,也就是我们起步的那一条横线 上,那这道题就简单很多了,我们可以将其转换为括号问题,因为其最终结果一定都是回到原点,那么我们就考虑将斜向上的问题看做“(”,斜向下的线条看作“)”,那这道题就好做了。
那我们如何说明其正确性呢?首先,我们不可能出现开局就一直往下的情况,且题目也不允许我们画到水平线下方,那么我们就基本可以排除遇到“)”而没有“(”的情况了,还是前面的证明,因为数目相同,所以肯定会两两配对,因此以做括号问题的思路做是完全没有问题的。
无法穿越的对角线
题面:有一个 n*n 的网格图,我们从(1,1)开始,一直要走到(n,n),且不能走到网格图的上方(或下方,看题目要求),问有多少种走法。
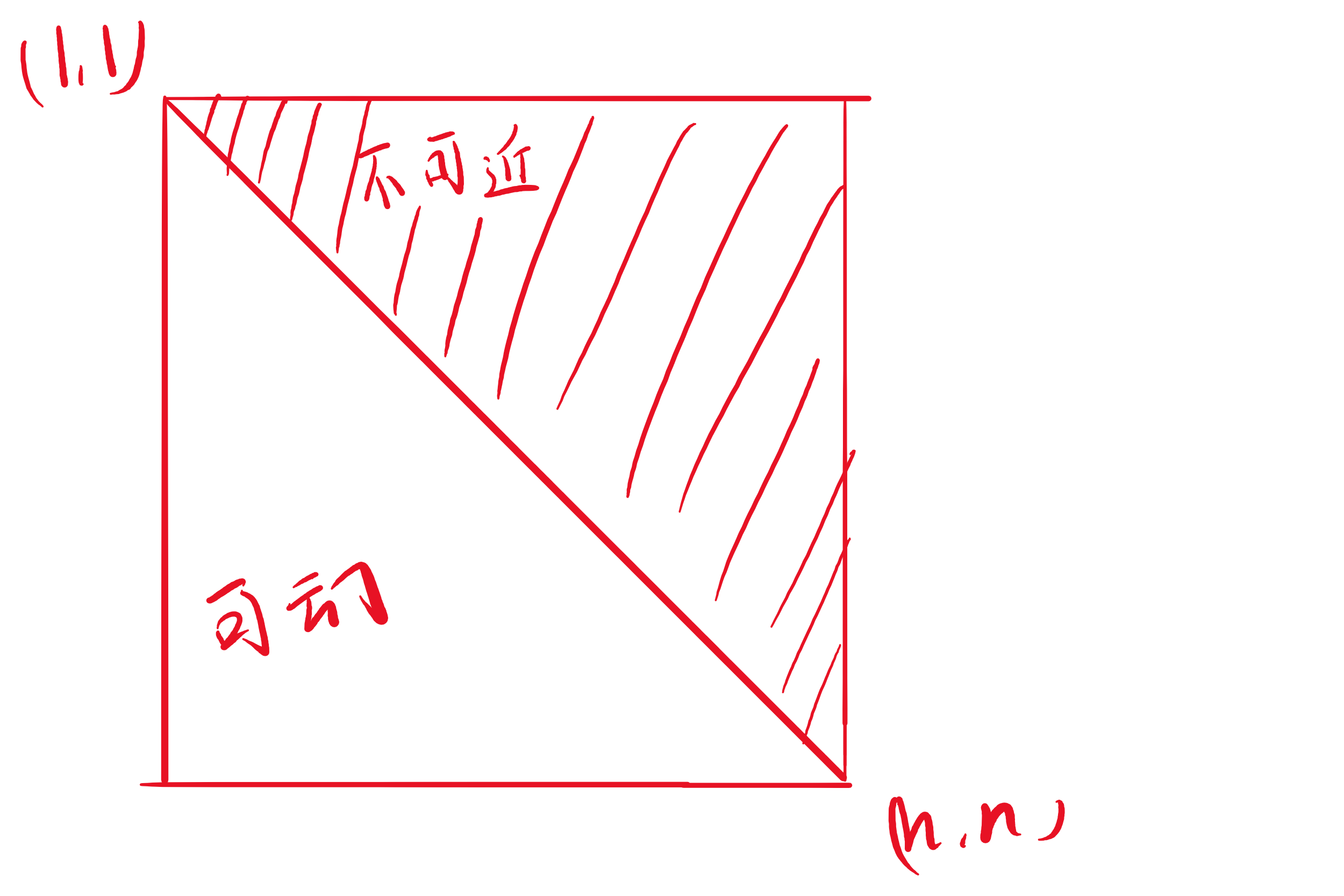
这便是题目大意。
我们依旧是枚举一下,当 n =4 时 ,结果为 14 。
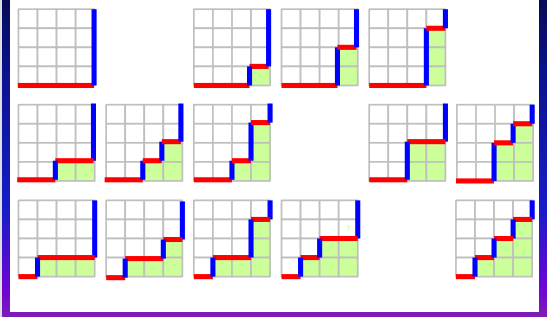
但是,枚举是一回事,如何算出正确的结果又是一码事了,我们能像前面那样将题目转换为之前的某种知识点呢?
答案是可以的,假如我们将图逆时针旋转135度,这时候我们能得到群峰模型:
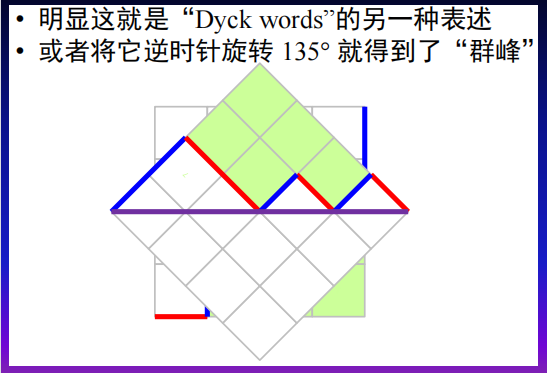
我们就可以通过群峰的做法来做了。
再探群峰问题
我们转回头再看看群峰问题,之前我们是没有严谨地解决过题目的,这次我们就用群峰模型来讲讲如何做卡特兰数。
我们之前讲过群峰模型是肯定会回到水平面的,所以我们考虑分治为两个与自身情况相同但是规模变小的子问题。我们以水平线为标准,如果能碰到水平线,那么我们就将这个碰到水平线的位置作为一个分界线,左边是一个子问题,右边是一个子问题,如此分下去直到问题简单可解。
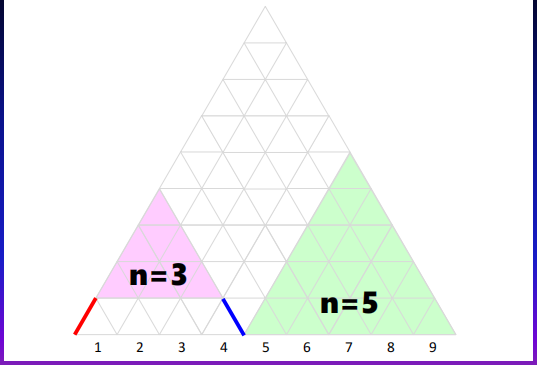
稍微解释一下这个图,我们将其分为两个部分,一个是左边的,一个是右边的,这两个子问题的数目总和就可以是n=9
那么为什么是 n-i-1呢,因为你会发现,我们其实是存在0,这个选项的,并且我们不可能取到n这个数,所以也就有了个-1.
我们前面讲题的时候,会发现这和卡特兰数是直接挂钩的,不错,这就是卡特兰数的递推式
我们看看能不能伸展一下,不能拘泥于一个递推式。
我们可以知道 C_n=\sum_{i=0}C_ix^i,我们可以得到C(x)*C(x)=(C(x)-1)/x,整理可得C(x)=1+x*C(x)^2,这是一个一元二次方程,我们用公式法就可以得到C(x)=\frac{1\pm\sqrt{1-4x}}{2x},不用在意根号下的数是否为正为负,因为在生成函数里是不需要要用一个具体的值来思考的,这时候我们验证一下,会发现正数那个值是错误的。
具体如何验证:由于我是个蒟蒻,不会用微积分对x→0取两式的极限,所以我们只能从稍微感性的角度理解。由于分母有一个2x,所以分子是没有常数项的,如果有常数项,就会出现形似于x^{-1}这种数,这是不被允许的,\sqrt{1-4x}的常数项是1,旁边也有个1,如果取正号的话,会得到2,所以我们需要一个1-1二分1+1。这就是为什么正号的值是错误的原因。
我们用一波牛顿二项式定理,整理得C(x)=\sum_{n=0}^{\infty}\tbinom{\frac{1}{2}}{n}\frac{x^n}{n+1},也就是C_n=\frac{1}{n+1}\tbinom{n}{2n},完全可用组合数做。
这就是著名的卡特兰数的组合数公式。
但是,我们在生活中用的更多的是这个公式的变形式:C(x)=\tbinom{n}{2n}-\tbinom{n-1}{2n}
但是这和我在做题时看到的样子不一样啊喂!他们都是要求我们不能低于什么数值的,或是极其隐晦地说出来,怎么可能那么简单地让你做出来?能看出这是卡特兰数已经是我的极限了喂!
我们简单地看这么道题:有一个长度为2n的01序列,其中1,0各n个,要求对于任意的整数k ∈ [ 1 , 2 n ],数列的前k个数中,1的个数不少于0。
毫无疑问,我们可以直接用第二个式子,但是我们还是得学习一下下面的这个思想。
不知道哪位神仙把它丢进了笛卡尔坐标系中,是1的就是向上走,是0的就是向下走,我们不能有-1以下的数 ,开始时肯定是(0,0),结果也一定是(2n,0),作图就是这样:
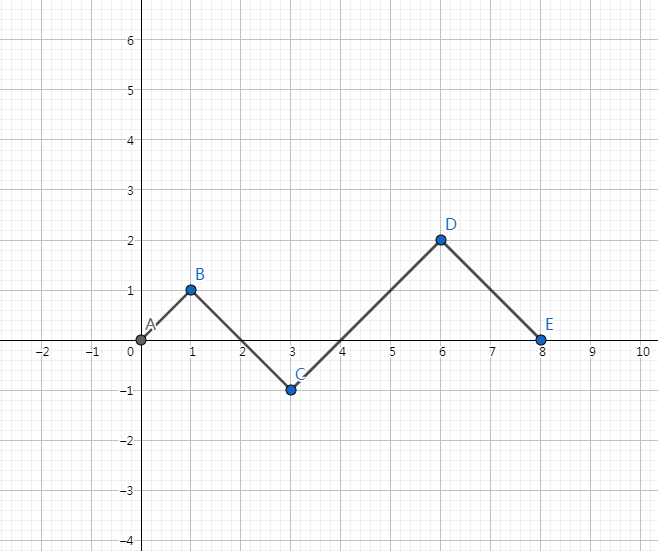
当然,这是个伪作图,因为合法的方案中没有-1的。
我们是不可能接触到 y=-1 这一条线的,但是我们还得试一下,所以我们试着将第一个与y=-1相交的点后面的部分以y=-1对称下去。
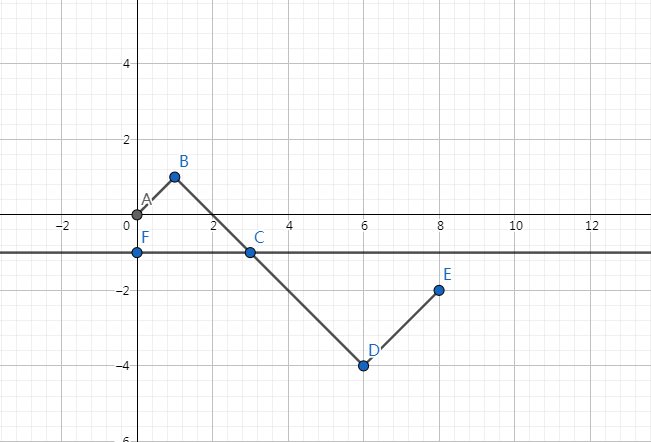
此时,我们是必定会经过y=-1的,所以我们用一下容斥原理,用总方案数减去不符合的方案数,这就是最终的答案。
此时的路径数量也不是特别难求,由于终点向下移了两位,所以此时终点在(2n,-2)的位置,所以不符合要求的方案为C\tbinom{n-1}{2n},故最终答案就是C\tbinom{n}{2n}-C\tbinom{n-1}{2n}.
这,就是卡特兰数。
(感谢@
(资料引自北京交通大学的课件,以及


 浙公网安备 33010602011771号
浙公网安备 33010602011771号