一种在每一步选择中都采取当前状态下最优选择的算法，通过局部最优解逐步构建全局最优解。文章介绍了贪心算法的概念、特点（局部最优选择、无后效性、近似最优解）及其应用场景（零钱找回、背包问题、哈夫曼编码等）。同时指出其局限性——不能保证全局最优解。通过多个具体问题（部分背包、排队接水、线段覆盖等）的代码实现，展示了贪心算法的实际应用策略和解题思路。最后以"铺设道路&就是贪心算法

贪心算法的介绍

贪心算法的概念：

是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。贪婪算法解决问题的过程中，作出的选择不能回溯，即一旦作出这些选择，就将其确定下来，不会再改变。

贪婪算法的特点：

贪婪算法通常用于求解最优化问题，其核心在于如何选择贪婪策略，使得局部最优能够导致全局最优。

贪婪算法的特点包括：

• 局部最优选择：在每一步都采取当前状态下最优的选择，不考虑整体最优解。

• 无后效性：一旦某个阶段的选择确定，就不会影响之前的选择，也不会影响之后的选择。

• 近似最优解：贪婪算法不能保证总能得到全局最优解，但在很多情况下能得到近似最优解。

贪婪算法的应用：

贪婪算法适用于具有最优子结构的问题，即一个问题的最优解包含其子问题的最优解。贪婪算法的应用范围非常广泛，包括但不限于：

• 零钱找回问题：在支付时尽可能使用大面额的货币，以减少货币的数量。

• 背包问题：在背包容量限制下，尽可能装入总价值最高的物品。

• 哈夫曼编码：用于数据压缩，根据字符出现频率来构造最优前缀码。

• 单源最短路径问题：如Dijkstra算法，用于在加权图中找到从单个源到所有其他顶点的最短路径。

• 最小生成树问题：如Prim算法和Kruskal算法，用于找到一个网络的最小生成树。

贪婪算法的局限性：

尽管贪婪算法在很多问题中都能得到满意的解，但它也有局限性。贪婪算法不一定能得到全局最优解，因为它没有考虑所有可能的解决方案。因此，在使用贪婪算法时，需要先分析问题是否适合使用贪婪策略。

最优子结构：每一步贪心选完后会留下子问题，子问题的最优解和贪心选出来的解可以凑成原问题的最优解

• 子问题是与原问题相似的一个规模较小的问题。

• 每次在某个问题上进行贪心选择后，就会产生原问题的一个子问题。打个比方：在任务安排问题中，“在某一个时间段上选择尽可能多个相容的任务”是原问题，经过“贪心选择”出一个任务后，余下的时间就比原来变少了，“在余下的时间段上选择尽可能多个相容的任务”就是一个子问题。

• 贪心选择性保证了：依照给定算法，在原问题上进行贪心选择时，选出的局部优化选择一定是（整体）最优解的一部分。例如任务安排问题中，选择结束时间最早的任务，对于整体而言一定是最好的。（当然这是从感性角度理解的贪心选择性，实际上需要严格证明）

• 而优化子结构则保证了：由贪心选择性得到的局部优化解和子问题的优化解相结合，可以获得整体优化解。这里可能有些难理解，其实从递归的角度来理解可能比较好。

部分背包：

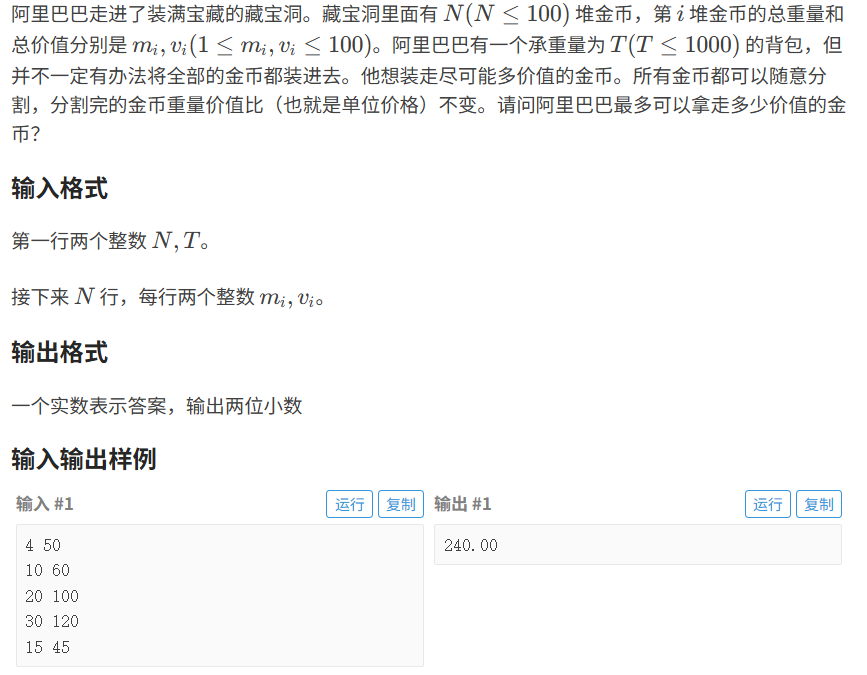
题目分析：

• 题目的意思是我有一个背包可以背T的重量的金币
• 现在有N堆金币   mi（重量）  vi（价值）
• 现在求能装的最大价值（金币堆可以拆解）

问题的切入点在于，金币堆是可以进行拆解的这样的话 可以统计一下每个金币堆单价

我们从价值高拿到价值低的拿金币堆即可

• 从价值高------>到价值低
•  金币堆的重量<=背包的重量 直接装进去 然后减去金币堆的重量  轮到下一个金币堆
• 金币堆的重量>背包的重量  把背包剩余重量*这个金币堆的单价 然后退出

相应程序：

#include
#include
#include
using namespace std;
double n,t;
double num=0;//统计金币个数
struct G{
float m;//重量
float v;//总价值
double k;//单价 因为可以拆分所以可以进行拆解
};
G g[105];//保存金币堆
bool cmp(G p1,G p2){ //仿函数 从大到小排序
return p1.k>p2.k;
}
int main(){
cin>>n>>t;
for(int i=0;i>g[i].m>>g[i].v;
g[i].k=g[i].v/g[i].m;//计算单价
}
//根据单价进行从小到大排序
sort(begin(g),end(g),cmp);
//开始拿金币
for(int i=0;i=0;){
if(g[i].m<=t){ //如果背包的重量大于金币堆的重量
num+=g[i].v; //直接装进去
t-=g[i].m;//减去重量
i++;//进入下一个金币堆
}
else{ //否则
num+=g[i].k*t;//直接加上剩余重量*单价
break;
}
}
cout<

排队接水

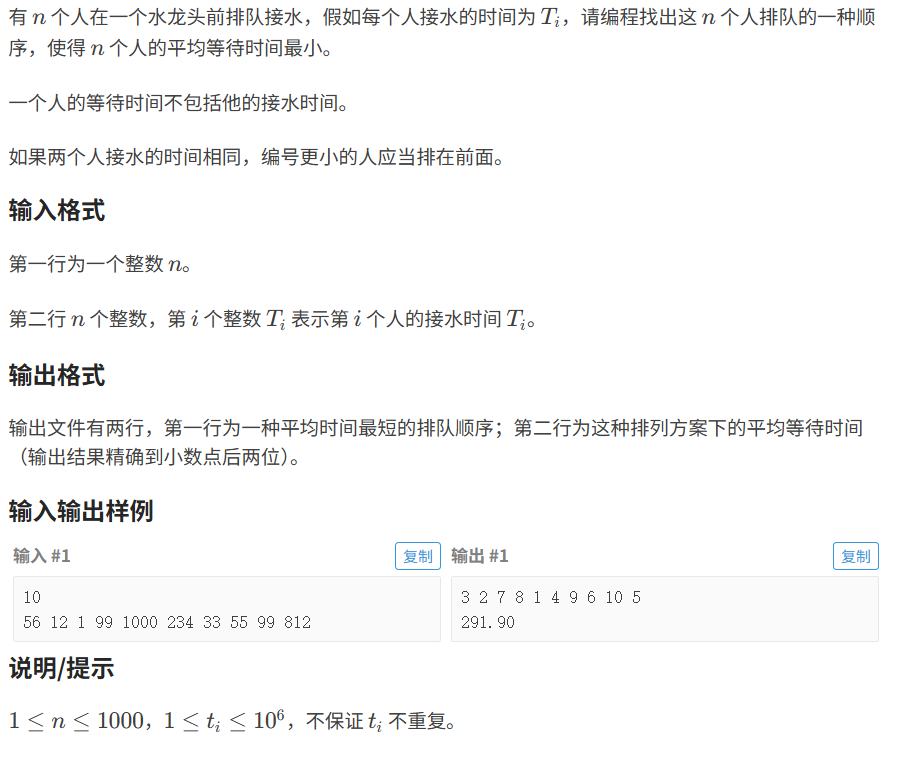
题目分析：

• 题目的意思是现在有 n个人在一个水龙头上接水 每个人的接水时间为 Ti 
• 一个人在接水的时候，其他人都在等待
• 自己在接水的时候不算等待时间，
• 求最短的排队时间。

因为当一个人打水时 剩下的人都要等待 

假设我有5个人等待时间为： 5 4 3 2 1

假设我让时间长的人先打水总的时间为:

5*4+4*3+3*2+2*1  

假设我让时间短的人先打水总的时间为:

1*4+2*3+3*2+4*1

解题过程：

• 创建结构体  包含接水时间和编号
• 使用sort（）对数据进行排序（从小到大）
• 计算等待时间  第一个乘数从 0开始   第二个乘数从n-1（表示剩余人数）开始
• 输出编号
• 输出接水的平均等待时间

相应程序：

#include
#include
#include
using namespace std;
int n;
//保存每个人的等待时间和编号
struct person{
int time;
int id;
};
double b=0;//保存等待时间
bool cmp(person p1,person p2){ //排序的规则
if(p1.time==p2.time) return p1.id>n;
person p[n+5];
for(int i=0;i>p[i].time;
p[i].id=i+1;
}
sort(p,p+n,cmp);//排序
int num=0;//从头开始遍历
for(int i=n-1;i>0;i--){
b+=p[num++].time*i;
}
//输出编号
for(int i=0;i

线段覆盖：

题目分析：

• 题目的意思是，有一个人要参加比赛   
• 现在有n个比赛  分别给出开始的时间和结束的时间
• 一次只能参加一个比赛  求这个人能参加几个比赛？

举个例子：

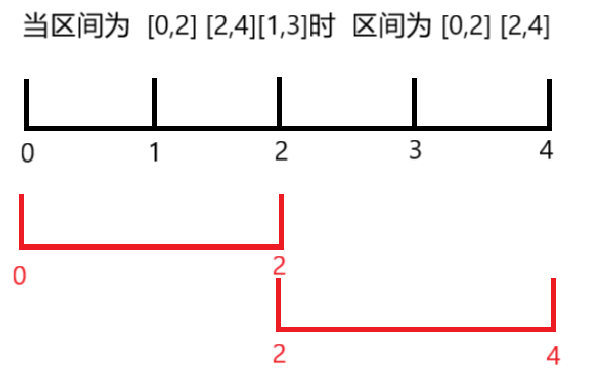
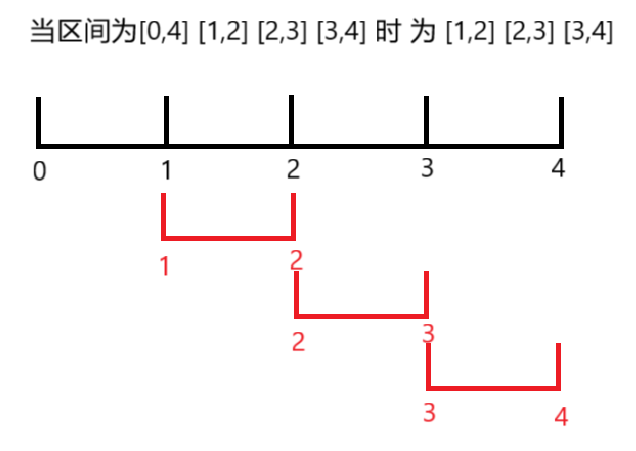
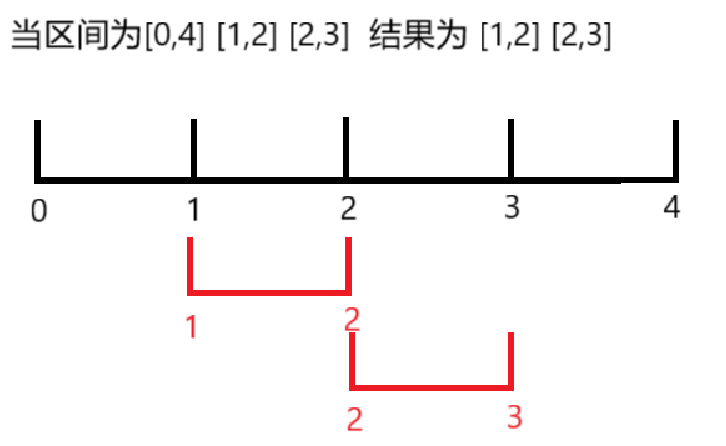
我们尽量要让坐标轴不相交的区间数多

到底该怎么贪呢？

• 首先我们用的这几个坐标区间肯定是不相交的
• 相交的条件：第二个区间的起点在 第一个区间的范围内（当我们按照起点选数的时候很容易出现这种情况）
• 如何选择区间呢？首先区间多 区间的起点和终点多
• 使用起点的话不好判断，这里使用区间的终点进行判断（这样妨碍比较少）
• 我们可以按照区间的终点从小到大进行排序，初始边界index为0，如果插入未相交（left>=index）个数+1，更新边界 index=right;

相应程序：

#include
#include
using namespace std;
struct P{ //记录每个区间的起点和终点
int left;
int right;
};
int n;//比赛的个数
int number=0;//能参加比赛的个数
bool cmp(P p1,P p2){ //按照终点从小到大排序
return p1.right>n;
P p[n+5];
int max=-1;
for(int i=0;i>p[i].left>>p[i].right;
}
sort(p,p+n,cmp);
//开始选赛
int index=0;//起始边界为0
for(int i=0;i=index){//如果可以插入
number++;//个数+1
index=p[i].right;//更新边界
}
}
cout<

合并果子：

题目分析：

题目的意思是：将几堆果子进行合并 每次只能合并两个，求花费的最小体力。

• 合并的时候需要选择最轻的两个堆进行合并这样是最省体力的
• 每次合并完需要删除这两个数据，将合并后的数组添加到数组中
• 这里使用STL 中的 multiset这个容器 头文件#include<set>
• 每次插入数据时都会将数据排好序（默认从小到大排序）
• 访问元素需要使用迭代器 
• 用完数后使用 erase()删除元素

相应程序：

#include
#include //可以保存相同的数 每次插入和删除都可以保持数据有序
#include
using namespace std;
int n;
long long num=0;//计算体力消耗
int main(){
cin>>n;
multiset mset;
for(int i=1;i>a;
mset.insert(a);
}
for(int i=1;i

小A的糖果

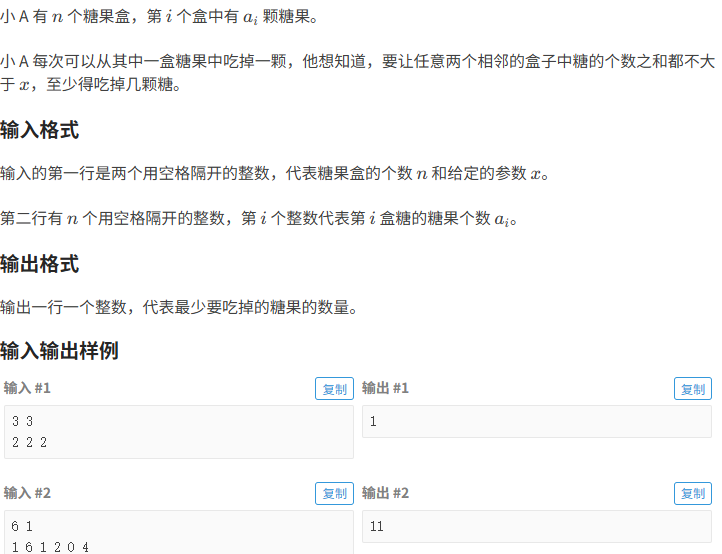
题目分析：

简单来说就是判断任意两个相邻的数之和<=指定的数

需要判断的情况为:

• 当两个数的和 <= 指定的数时   不需要处理
• 当两数的和 > 指定的数时 分两种情况
  • 当右边的数够时，仅删除右边的数即可
  • 当右边的数不够时，先删除右边的数，再删除左边的数

相应程序：

#include
using namespace std;
int n,x;
long long number=0;//需要吃掉的糖果数
int main(){
cin>>n>>x;
long long arr[n];
for(int i=0;i>arr[i];
}
//优先吃掉右边的盒子
for(int i=0;ix){ //和大于 x
if(arr[i]<=x){ //如果第一个数<=x 只需要处理第二个数即可
arr[i+1]-=n1-x;
number+=n1-x;
}
else{ //需要处理两个数
arr[i]=x;
arr[i+1]=0;
number+=n1-x;
}
}
}
cout<

删数问题：

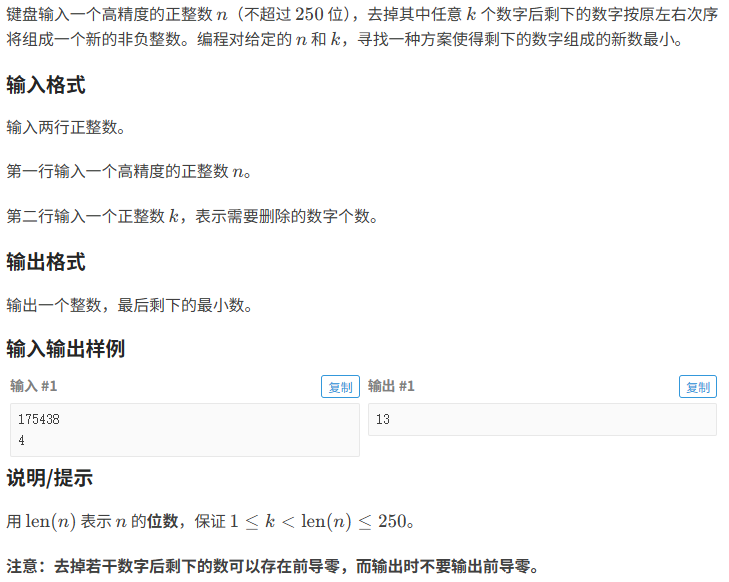
题目分析：

题目的意思是：给出一个数  删除n个数 使其剩下的值最小

举个例子：

我们以删除一个数为例：

这个例子中可以得到的信息：删除最大的那个数不一定是相应的结果

这时候需要找相应的规律了

当第一位数 >第二位数  直接把第二位数删除

当第一位数 <=第二位数    往下面继续寻找（递归）

在这里可以总结以下规律：

从头到尾  找相邻两个数  找到第一个数大于第二个数的位置   把第一个数的位置删掉即可

• 需要特判的是当数据都相同时    直接删除最后一个数据
• 因为每一位数都为0-9  所以0是最小的值  所以不需要特别处理

相应程序：

#include
#include
using namespace std;
string s;//字符串
int n;//个数
int main(){
cin>>s;
cin>>n;
if(n>=s.length()) couts[i+1]){
index=i;break;
}
}
if(index==-1){ //没找到直接
s.erase(--s.end());//删除最后一个数据
}
else{
s.erase(s.begin()+index);//删除指定位置的数据
}
}
}
//不输出前置0 找第一个
bool b=true;
for(int i=0;i

铺设道路

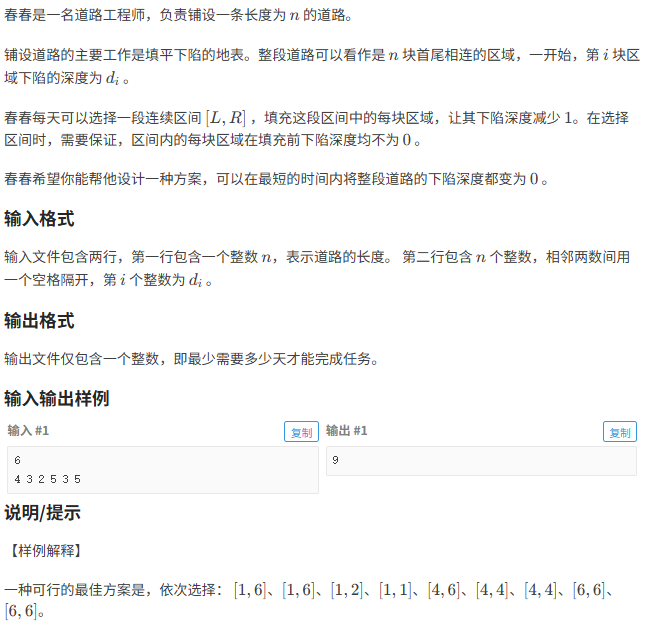
题目分析：

• 现在有n个坑  每个坑高度不一样 
• 现在要填坑   可以在一个区间上填（说人话就是连续的坑） 每次填1
• 要求每个坑都填满  但坑不能溢出（到0就不可以填了）
• 求要填多少次

根据题目给出的样例解释：是每次选最长的区间进行处理直到全部坑的值为0结束

如果按照题目的要求 每次都要找到最大的那个区间  

• 方法一：每次遍历数组找到最大的那个区间 (暴力解法，时间消耗比较大)
• 方法二：使用容器去装0的下标，然后去找大区间（空间消耗比较大，需要存储点位）

暴力求解（70/100）超时：

#include
int n;
int number=0;//统计填充的次数
using namespace std;
int main(){
cin>>n;
int arr[n+5];
for(int i=1;i>arr[i];
}
//每次找最长连续的区间
while(1){
int lt=-1;
int rt=-1;
int left=-1;//左边界
int right=-1;//右边界
int num=-1;//区间长度
for(int i=1;inum){
lt=left;
rt=right;
num=right-left+1;
}
left=-1;right=-1;num=-1; //判断完重置
}
}
if(left!=-1){ //当右侧没有0时 直接添加n
lt=left;
rt=n;
}
if(lt==-1&&rt==-1) break;//如果没找到直接退出
//开始填充
for(int i=lt;i<=rt;i++){
--arr[i];
}
number++;
}
cout<

暴力优化（100/100）超时：

根据题目给出的求解，我们只需要计算消耗的天数即可，不需要输出每次执行的过程。

在统计天数这个过程中其实 没必要一定要执行当前数据中的最长的连续区间。

解题的过程：

• 当数组中不存在0，直接处理整个数组  需要涂抹的次数是 数组中的最小的非0值
• 当数组中存在0，找最近的一个连续区间（边界为 0  或数组的边界）
• 当边界的长度为1时 直接涂抹对应的数组值即可

相应程序：

#include
int n;
int number=0;//统计粉刷的次数
using namespace std;
int main(){
cin>>n;
int arr[n+5];
for(int i=1;i>arr[i];
}
for(int i=1;iarr[i]&&arr[i]!=0) min_data=arr[i];//获取区间非0的最小值
if(arr[i]!=0&&left==-1) left=i;
if(arr[i]==0&&left!=-1){
right=i-1;//找到右边界直接退出循环
break;
}
}
if(left==-1&&right==-1) break;//结束
if(left!=-1&&right==-1) right=n;//右边界处理
num=right-left+1;//获取区间长度
cout<

贪心的做法：

假设我现在有一个坑arr[n1]  旁边又有一个坑arr[n2]

分析方法1：

• 当 arr[n1]>arr[n2] 那么涂抹的时候   n2顺手就被涂抹掉(不需要消耗次数)   
• 这个坑需要填的次数是：sum+=arr[n1]-arr[n2]
• 判断相邻两个数据  if(n1>n2) sum+=arr[n1]-arr[n2] 由于最后一个数据没有后面的数据，直接添加就行  sum+=arr[n];

分析方法2：

• 当 arr[n1]<arr[n2] 那么涂抹的时候   arr[n1]顺手就被涂抹掉了   
• 这个坑需要填的次数是：sum+=arr[n2]-arr[n1]
• 判断相邻两个数据  if(n1>n2) sum+=arr[n1]-arr[n2] 由于第一个数据没有后面前面的数据，直接添加就行  sum+=arr[1];

相应程序：

#include
using namespace std;
int n;
int arr[100005];
long long ans=0;
int main(){
cin>>n;
for(int i=1;i>arr[i];
for(int i=2;iarr[i-1]) ans+=arr[i]-arr[i-1];
cout<