算法竞赛——树和图的存储与遍历
一、树与图的存储方式
树(无环连通图)、图的存储:
有向图:
a ---> b 无向图:
a ---> b,b ---> a无向图可以看作是特殊的有向图!
1.邻接矩阵
稠密图一般使用邻接矩阵存储,空间复杂度达到(n * n)
存储方式:
g[b][b]存储a ---> b的信息,如果有权值c则g[b][b] = c;如果没有权值则为bool,表示是否连通注:邻接矩阵不能存储重边,一般只保留一条(最短的:如朴素dijkstra算法和prim算法)
2.邻接表
邻接表适用于存储稀疏图,是一种最常用的图存储方式:对于每一个节点,都开一个单链表(类似拉链法)存储该节点可以访问到的点,存储次序无关紧要。
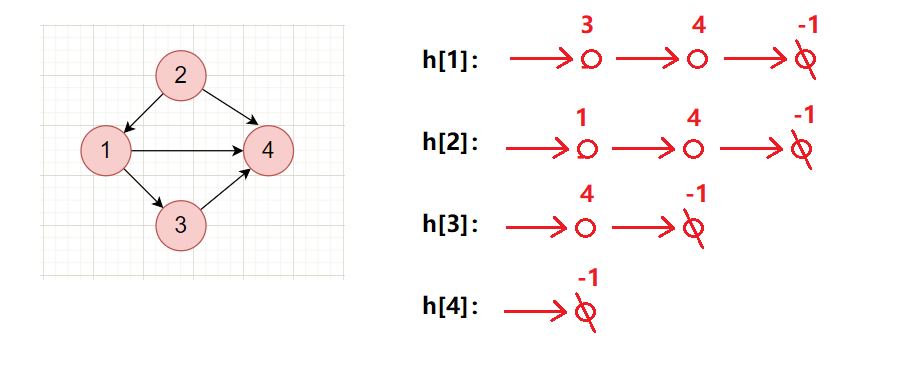
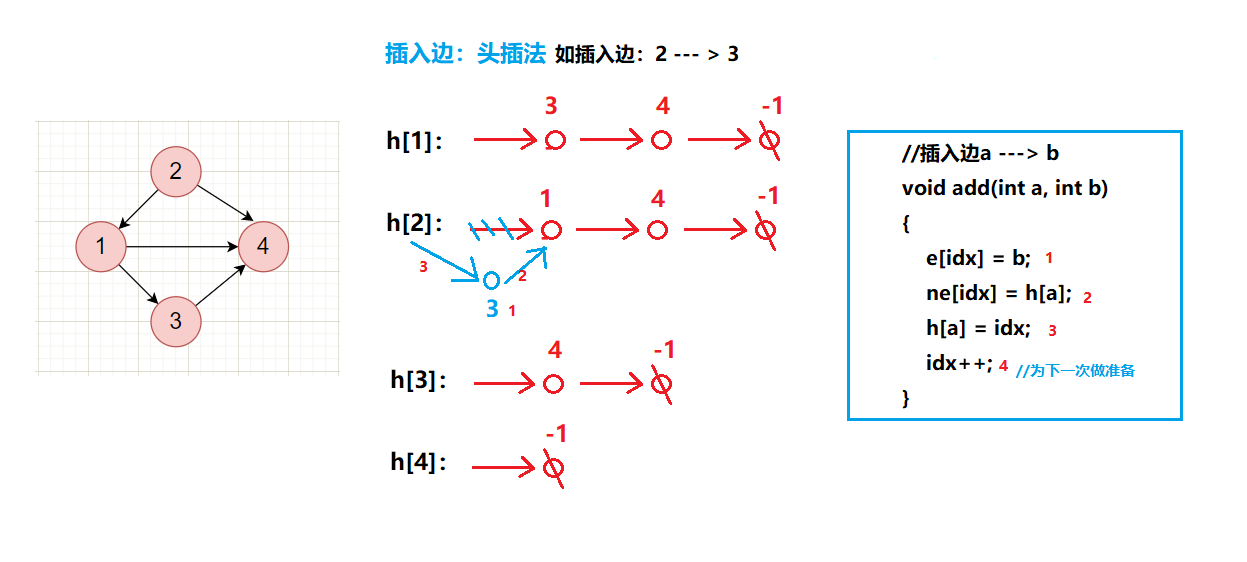
插入边:
初始化链表:
memset(h, -1, sizeof h);
插入操作:
不带权值:
//邻接表
int h[N], e[M], ne[M], idx;// M = 2 * N
//插入边a ---> b
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
带权值:
int h[N], w[N], e[N], ne[N], idx;
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a]. h[a] = idx ++;
}
二、树与图的遍历方式
1.深度优先遍历
(1)图的深度优先遍历框架模板:
//u为节点编号
void dfs(int u){
st[u]=true; // 标记一下,记录为已经被搜索过了
// 遍历u的邻接点
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];//拿到出边的对应的节点编号
if(!st[j])//如果未被访问过,继续深搜
{
dfs(j);
}
}
}
(2)例题:树的重心
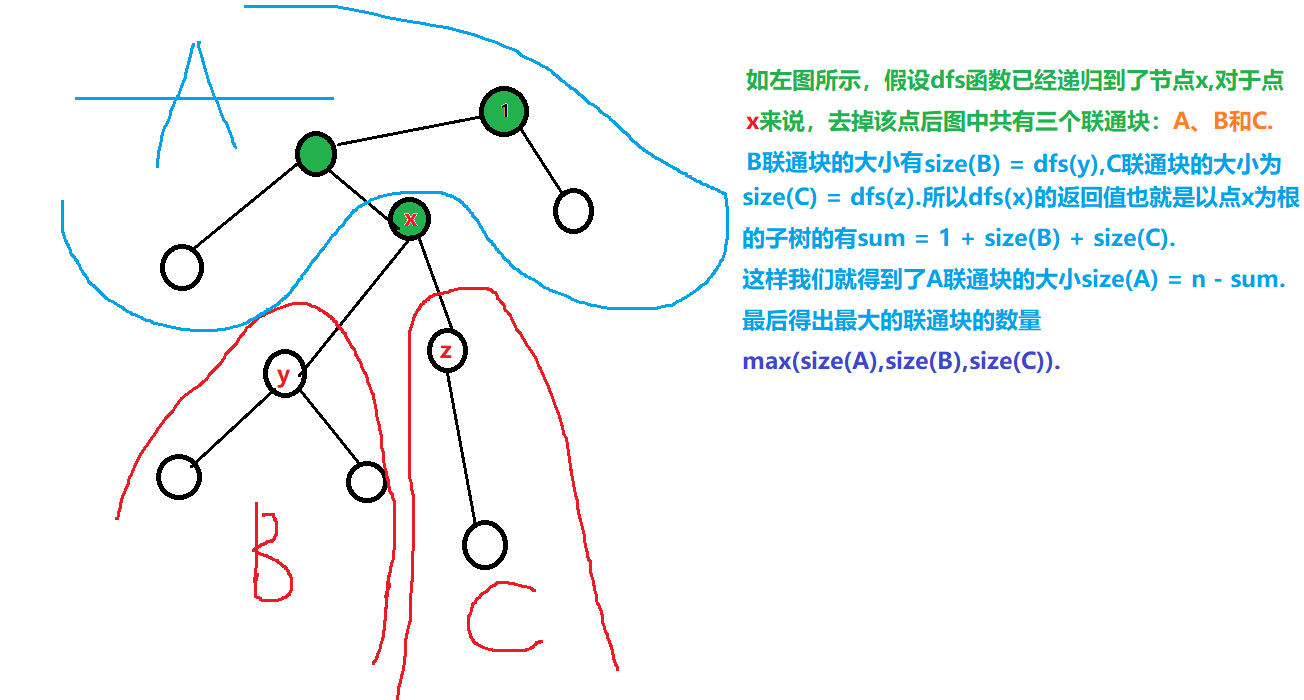
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int n;
int h[N], e[M], ne[M], idx;
int ans = N;
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx, idx ++;
}
//返回以u为根节点的子树中节点的个数,包括u节点
int dfs(int u)
{
st[u] = true;// 标记一下,已经搜索过
//size是表示将u点去除后,剩下的子树中数量的最大值;
//sum表示以u为根的子树的点的多少,初值为1,因为已经有了u这个点
int size = 0, sum = 1;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];//拿到出边的对应的节点编号
if(!st[j])
{
int s = dfs(j); // 当前子树的大小(//s是以j为根节点的子树中点的数量)
size = max(size, s);// 取子树种节点数较大者
sum += s;
}
}
//n-sum表示的是减掉u为根的子树,整个树剩下的点的数量
size = max(size, n - sum);
ans = min(ans, res);
return sum;
}
int main()
{
cin >> n;
//初始化链表
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);//无向图
}
//从第一个节点开始搜索
dfs(1);
printf("%d\n", ans);
return 0;
}
2.广度优先遍历
图宽搜的框架和前面BFS的框架基本一模一样,只是将图的结构扩展到宽搜框架里。前面的BFS是根据具体题目来扩展点,图的话采用邻接表存储图,从1号节点编号开始,扩展的是每一个点的临边。
(1)图的广度优先遍历框架模板:
1. queue <---- 1号点
2. while(队列不为空)
{
t <---队头
弹出队头
扩展队头元素(扩展t的所有邻接点j)
{
获取邻接点(编号)j
if(j未遍历,符合条件)// 第一次遍历才是最短路径
{
queue <----- j入队// (邻接节点)
更新距离 //d[x] = d[t]++
}
}
}
3. 最后队为空,结束
(2)例题:图中点的层次
给定一个 n 个点 mm条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1∼n。
请你求出 1号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点,输出 −1。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
数据范围
1≤n,m≤105
输入样例:
4 5 1 2 2 3 3 4 1 3 1 4输出样例:
1
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int d[N];//存储点到起点的距离
int n, m;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int bfs()
{
//初始化距离,且起用于判断是否访问过
memset(d, -1, sizeof d);
//1.一号节点(编号)入队,设置距离
queue<int>q;
q.push(1);
d[1] = 0;
//2.队列不为空
while(q.size())
{
//2.1拿到队头节点,队头出队
auto t = q.front();
q.pop();
//2.2扩展队头元素(t的所有邻接节点)
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];//得到邻接节点j
if(d[j] == -1)//如果j节点没有被访问过
{
q.push(j);//入队
d[j] = d[t] + 1;//更新距离
}
}
}
//3.返回结果
return d[n];
}
int main()
{
cin >> n >> m;
//初始化链表
memset(h, -1, sizeof h);
while (m -- )
{
int a, b;
cin >> a >> b;
add(a, b);
}
cout << bfs();
return 0;
}
(3)图广搜的应用——拓扑排序
基本介绍:
拓扑序列:在一个有向图无环中,对所有的节点进行排序,要求没有一个节点指向它前面的节点。即,所有的边从前指向后!
注:无向图没有拓扑序列
入度:一个点有多少条进来(指向自己)的边
出度:一个点有多少条出去(指向其它点)的边
重要结论性质:一个有向无环图至少存在一个入度为0的节点!
求解步骤:
(1)先统计好图中所有点的入度情况
(2)找到图中入度为0的节点,将它删去,由它发射出来的所有边也要删掉,即它指向的邻接节点度数-1
(3)将删去节点后剩下的图,继续按(2)的规则继续删节点。
按照节点被删除的顺序,依次把这些被删除的节点记录要一个序列里边,当图中所有节点被删除后,那么这个序列就是一个拓扑序列了!
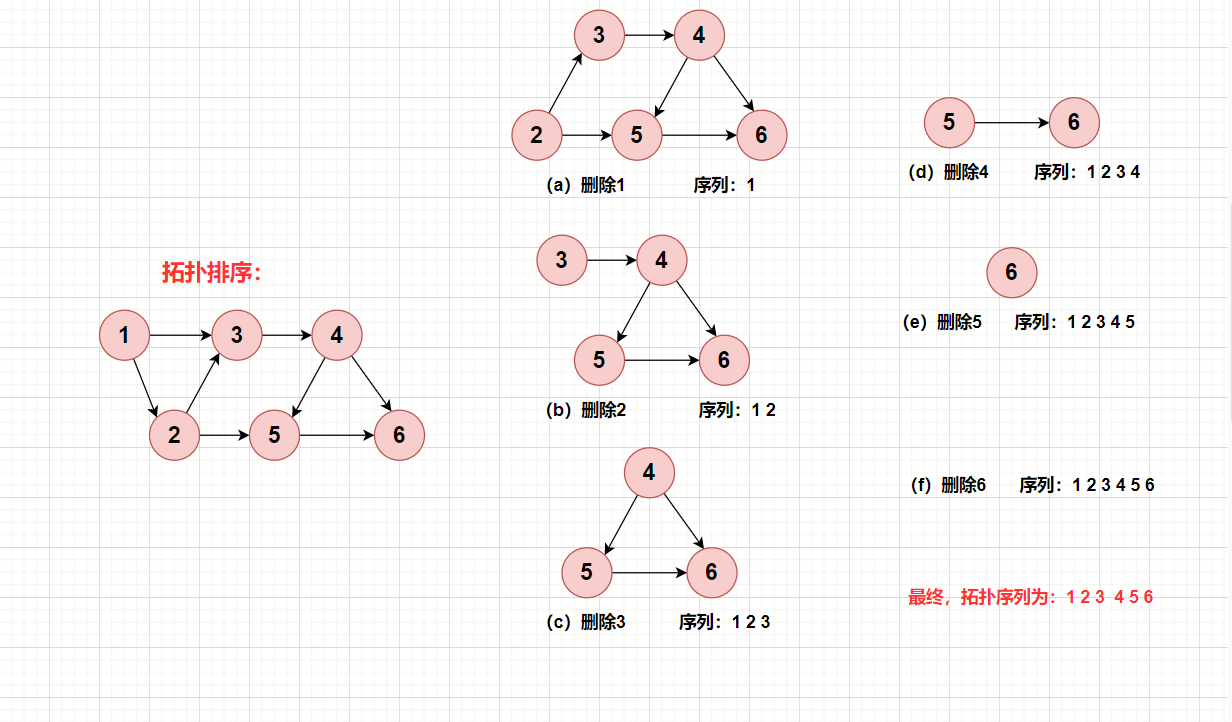
注:当同时出现两个或以上入度为0的节点时,拓扑序列结果不唯一!
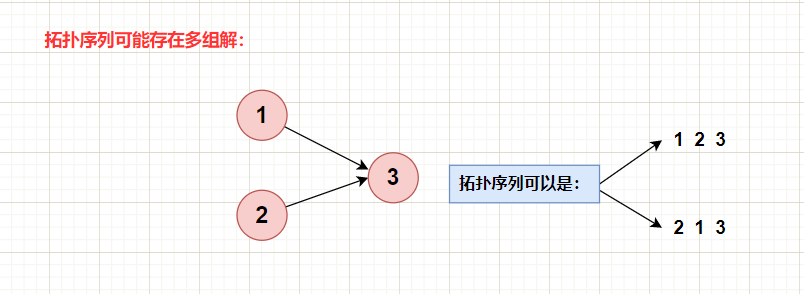
基本BFS框架:
bool topsort()
{
1. queue <---- 所有度为0的点
2. while queue不为空
{
t <---- 队头
弹出队头
枚举t所有的出边 t ---> j
{
删掉出边 t ---> j: d[j] --;// 入度-1
if(d[j] == 0)// 当节点j入度为0时,入队
queue <---- j
}
}
如果有n - 1个节点入队的话,说明是拓扑序列返回true,否则不是返回false
}
例题:
给定一个 n 个点 m 条边的有向图,点的编号是 1 到 n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 AA 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列。
输入格式
第一行包含两个整数 n 和 m。
接下来 mm 行,每行包含两个整数 x 和 y,表示存在一条从点 x 到点 y 的有向边 (x,y)。
输出格式
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 −1。
数据范围
1≤n,m≤105
输入样例:
3 3 1 2 2 3 1 3输出样例:
1 2 3
【参考代码】
数组模拟队列:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int d[N];//统计节点入度情况
int q[N];//队列
int n, m;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool topsort()
{
int hh = 0, tt = -1;
//1.
for (int i = 1; i <= n; i ++ )// 将所有入度为0的点入队
if(d[i] == 0)
q[++ tt] = i;
//2.
while(hh <= tt)
{
int t = q[hh ++];// 获取队头元素的同时,也就弹出了队头元素!
//删掉t的所有出边
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
d[j] --;
if(d[j] == 0)
q[++ tt] = j;//当节点j入度为0时,入队
}
}
return tt==n-1;
//表示如果n个点都入队了话,那么该图为拓扑图,返回true,否则返回false
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
while (m -- )
{
int a, b;
cin >> a >> b;
add(a, b);
d[b] ++;//因为是a指向b,所以b点的入度要加1
}
if(topsort())
{
for (int i = 0; i < n; i ++ )
cout << q[i] << " ";
//经上方循环可以发现队列中的点的次序就是拓扑序列
//注:拓扑序列的答案并不唯一
puts("");
}
else
puts("-1");
return 0;
}
STL:queue,开一个top[N]数组来记录拓扑序列!
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int d[N];//统计节点入度情况
int top[N];//记录拓扑序列
int n, m, cnt;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool topsort()
{
queue<int>q;
for (int i = 1; i <= n; i ++ )// 将所有入度为0的点入队
if(d[i] == 0)
q.push(i);
//2.
while(q.size())
{
int t = q.front();
top[cnt ++] = t;//加入到 拓扑序列中
q.pop();
//删掉t的所有出边
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
d[j] --;
if(d[j] == 0)
q.push(j);//当节点j入度为0时,入队
}
}
return cnt == n;
//表示如果n个点都入队了话,那么该图为拓扑图,返回true,否则返回false
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
while (m -- )
{
int a, b;
cin >> a >> b;
add(a, b);
d[b] ++;//因为是a指向b,所以b点的入度要加1
}
if(topsort())
{
for (int i = 0; i < n; i ++ )
cout << top[i] << " ";
//经上方循环可以发现队列中的点的次序就是拓扑序列
//注:拓扑序列的答案并不唯一
puts("");
}
else
puts("-1");
return 0;
}
三、总结
在理解思路的基础上,学习总结代码!
学习内容源自:
acwing算法基础课
注:如果文章有任何错误或不足,请各位大佬尽情指出,评论留言留下您宝贵的建议!如果这篇文章对你有些许帮助,希望可爱亲切的您点个赞推荐一手,非常感谢啦



 浙公网安备 33010602011771号
浙公网安备 33010602011771号