算法竞赛——BFS广度优先搜索
BFS
广度优先搜索:一层一层的搜索(类似于树的层次遍历)
BFS基本框架
基本步骤:
初始状态(起点)加到队列里
while(队列不为空)
队头弹出
扩展队头元素(邻接节点入队)
最后队为空,结束
BFS难点所在(最短路问题):
存储的数据结构:队列
状态如何存储到队列里边(以什么形式)?
状态怎么表示,怎么转移?
dist
如何记录每一个状态的距离
最短路问题:宽搜的优势是能找到最短(最小)路!(所有边权重都一样才可以用!)——一层一层的搜索(类似于树的层次遍历)。深搜可以保证我们走到终点,但不能确保是最短路。
搜索过程(层次遍历)如下:
(1)从图中的某个顶点出V发,访问V
(2)依次访问V的各个未曾访问过的邻接点
(3)分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问
(4)重复步骤(3)直至所有已被访问的顶点的邻接点都被访问到
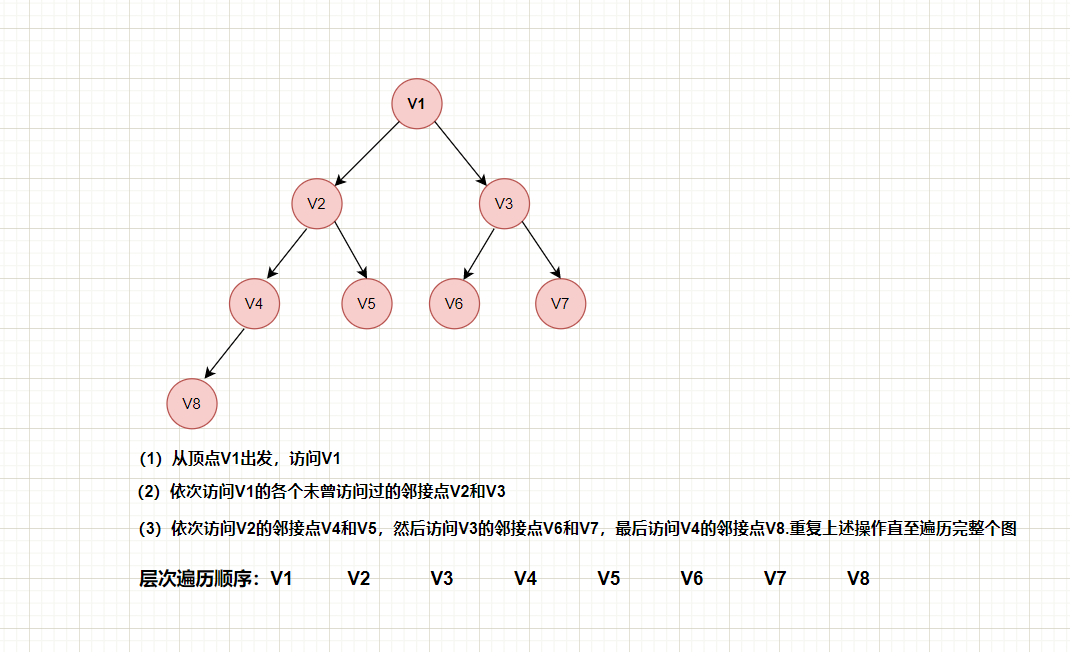
图的BFS和树几乎一模一样,唯一的区别是树有根节点,而图没有,因此在遍历图时要选一个根节点。下图以A作为根节点:
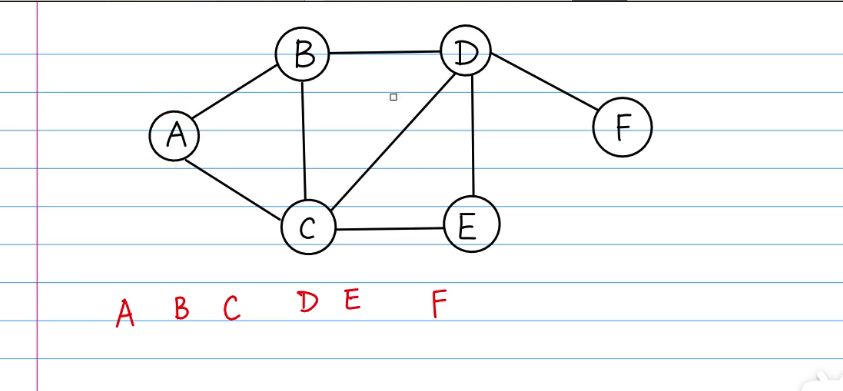
D和E是不能颠倒过来的,因为我们先遍历到的顶点是B,下一次展开的时候必须找与B直接相连的节点,即必须在找与C相连的节点之前把所有与B相连的节点找出来,由于A和C都走过了,因此唯一能走的点就是D。因此B先走完!
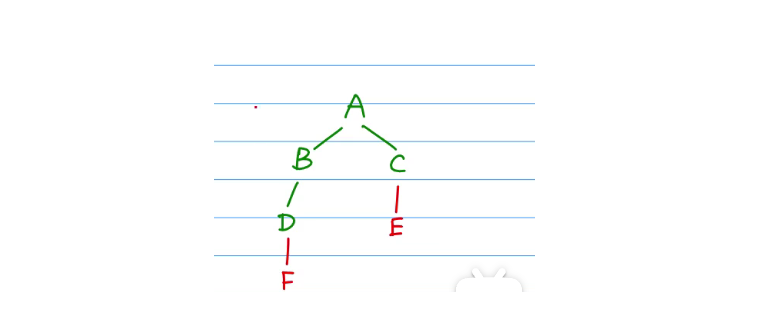
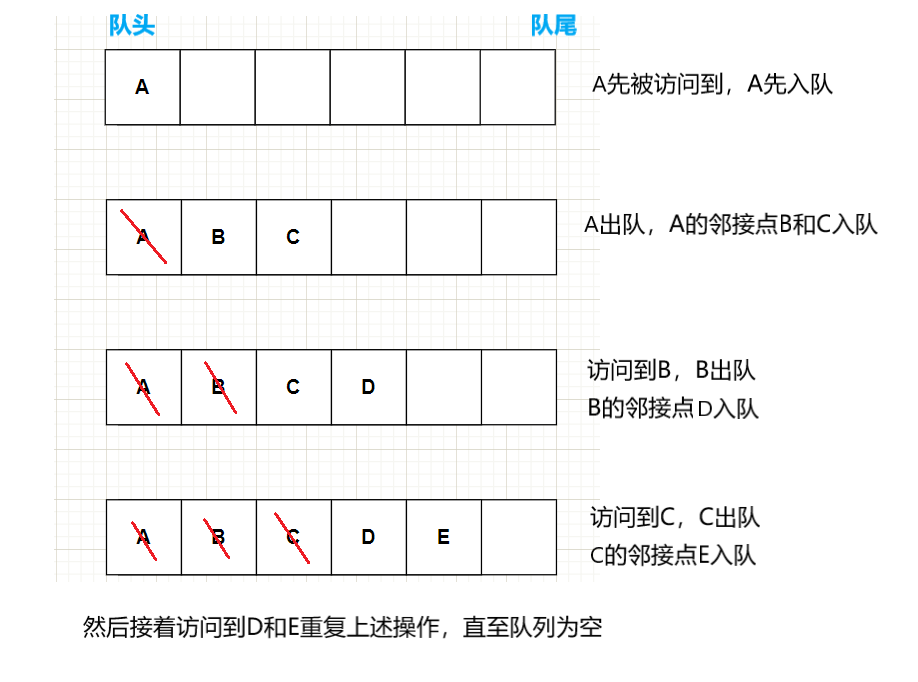
BFS的数据结构实现形式是队列,通过队列保存已被访问过的节点,利用其先进先出的特点:保证了先访问的顶点的邻接点亦先被访问
即队列保证了下图中B的邻接点比C的邻接点要先出现:
1.走迷宫(acwing 844)
给定一个 n×mn×m 的二维整数数组,用来表示一个迷宫,数组中只包含 00 或 11,其中 00 表示可以走的路,11 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1)(1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m)(n,m) 处,至少需要移动多少次。
数据保证 (1,1)(1,1) 处和 (n,m)(n,m) 处的数字为 00,且一定至少存在一条通路。
输入格式
第一行包含两个整数 nn 和 mm。
接下来 nn 行,每行包含 mm 个整数(00 或 11),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤1001≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0输出样例:
8
【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int>PII;//pair存放点的坐标
const int N = 110;
int g[N][N];//存放地图
int d[N][N];//存放点到起点的距离
// 四个方向!
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
int n, m;
int bfs()
{
queue<PII> q;//队列存储访问过的点以及该顶点的邻接点
memset(d, -1, sizeof d);//初始化各个点要起点的距离为-1,表示该点没有被访问过的
//1.起点入队
q.push({0, 0});
d[0][0] = 0;// 起点到自己的距离为0
//2.while(...)
while(q.size())
{
//2.1 获取队头元素 并弹出
auto t = q.front();// 拿到队头元素
q.pop();// 弹出队头元素
//2.2 扩展队头元素(邻接点入队)
for(int i = 0; i < 4; i ++)// 枚举所有邻接点
{
int x = t.first + dx[i];
int y = t.second + dy[i];
if(x >= 0 && y >= 0 && x < n && y < m && d[x][y] == -1 && g[x][y] == 0)// 判断是否满足条件
{
//该邻接点入队,距离增加
q.push({x, y});
d[x][y] = d[t.first][t.second] + 1;
}
}
}
return d[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
//输入地图
for (int i = 0; i < n; i ++ )
for(int j = 0; j < m; j ++)
cin >> g[i][j];
cout << bfs();
return 0;
}
数组模拟队列:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;
int n, m;
int g[N][N];//存放地图
int d[N][N];//存 每一个点到起点的距离
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//x 方向的向量和 y 方向的向量组成的上、右、下、左
PII q[N * N];//手写队列
int bfs()
{
int hh = 0, tt = 0;
q[0] = {0, 0};
memset(d, - 1, sizeof d);//距离初始化为- 1表示没有走过
d[0][0] = 0;//表示起点走过了
while(hh <= tt)//队列不空
{
PII t = q[hh ++ ];//取队头元素
for(int i = 0; i < 4; i ++ )//枚举4个方向
{
int x = t.first + dx[i], y = t.second + dy[i];//x表示沿着此方向走会走到哪个点
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//在边界内 并且是空地可以走 且之前没有走过
{
d[x][y] = d[t.first][t.second] + 1;//到起点的距离
q[ ++ tt ] = {x, y};//新坐标入队
}
}
}
return d[n - 1][m - 1]; //输出右下角点距起点的距离即可
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
for(int j = 0; j < m; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
2.八数码
在一个 3×33×3 的网格中,1∼81∼8 这 88 个数字和一个
x恰好不重不漏地分布在这 3×33×3 的网格中。例如:
1 2 3 x 4 6 7 5 8在游戏过程中,可以把
x与其上、下、左、右四个方向之一的数字交换(如果存在)。我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3 4 5 6 7 8 x例如,示例中图形就可以通过让
x先后与右、下、右三个方向的数字交换成功得到正确排列。交换过程如下:
1 2 3 1 2 3 1 2 3 1 2 3 x 4 6 4 x 6 4 5 6 4 5 6 7 5 8 7 5 8 7 x 8 7 8 x现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将 3×33×3 的初始网格描绘出来。
例如,如果初始网格如下所示:
1 2 3 x 4 6 7 5 8则输入为:
1 2 3 x 4 6 7 5 8输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1−1。
输入样例:
2 3 4 1 5 x 7 6 8输出样例
19
1、题目的目标

求最小步数 -> 用BFS
2、移动情况
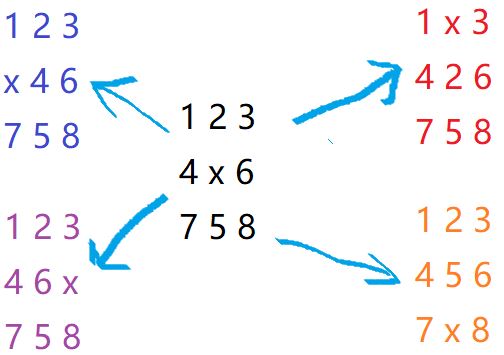
移动方式:
转以后:a = x + dx[i], b = y + dy[i].
思想:把每一个状态看作图论的一个节点(节点a到节点b的距离为1——状态能转移)——> 起点到终点最少需要多少步
从初始状况移动到目标情况 —> 求最短路
3、问题
第一点:状态如何存储到队列里?
第二点:如何记录每一个状态的“距离”(即需要移动的次数)?
第三点:队列怎么定义(队列存储的是状态,状态可以用字符串表示),dist数组怎么定义(每一个状态到起始状态的距离——两个关键字:状态(字符串)、距离(int))——key-value?——哈希表
4、解决方案
将 “3*3矩阵” 转化为 “字符串”
如:
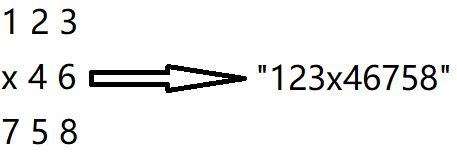
所以:
队列可以用 queue<string>
//直接存转化后的字符串
dist数组用 unordered_map<string, int>
//将字符串和数字联系在一起,字符串表示状态,数字表示距离
5、矩阵与字符串的转换方式

【参考代码】
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include<unordered_map>
using namespace std;
//状态转移
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int bfs(string strat)
{
//定义目标状态、
string end = "12345678x";
//定义队列和dist数组
queue<string> q;
unordered_map<string, int> d;
//初始化队列和dist数组
q.push(strat);
d[strat] = 0;
while(q.size())
{
// 获取队头元素,弹出队列
auto t = q.front();
q.pop();
//记录当前状态的距离,如果为最终状态则返回距离结果
int distance = d[t];
if(t == end) return d[t];
//查询x在一位数组中的下标,进行状态转换
int k = t.find('x');
int x = k / 3, y = k % 3;
//扩展队头元素(邻接节点入队)
for(int i = 0; i < 4; i ++)
{
//转移后的x的坐标(邻接节点)
int a = x + dx[i], b = y + dy[i];
//没有越界
if(a >= 0 && b >= 0 && a < 3 && b < 3)
{
//转移x
swap(t[k], t[a * 3 + b]);
//如果当前状态是第一次遍历,记录距离,入队
if(!d.count(t))
{
d[t] = distance + 1;
q.push(t);
}
//还原状态,为下一种转换情况做准备!
swap(t[k], t[a * 3 + b]);
}
}
}
//无法转换到目标状态,返回-1
return -1;
}
int main()
{
string strat;
// 输入起始状态
for (int i = 0; i < 9; i ++ )
{
char c;
cin >> c;
strat += c;
}
cout << bfs(strat);
}
总结常用技巧:一维数组与二维数组坐标的转换
设[一维数组]下标为index(从0开始),二维数组长度为m * n,则:
一维数组转换为二维数组
x = index / n
y = index % n
二维数组转换为一维数组
index = x + y * n
学习内容部分转载自:
1. acwing算法基础课
2.作者:四谷夕雨
链接:https://www.acwing.com/solution/content/15149/
注:如果文章有任何错误或不足,请各位大佬尽情指出,评论留言留下您宝贵的建议!如果这篇文章对你有些许帮助,希望可爱亲切的您点个赞推荐一手,非常感谢啦



 浙公网安备 33010602011771号
浙公网安备 33010602011771号