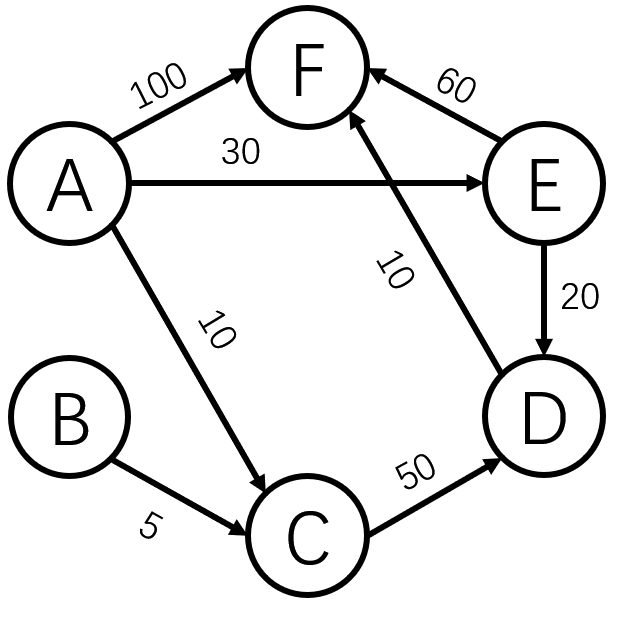
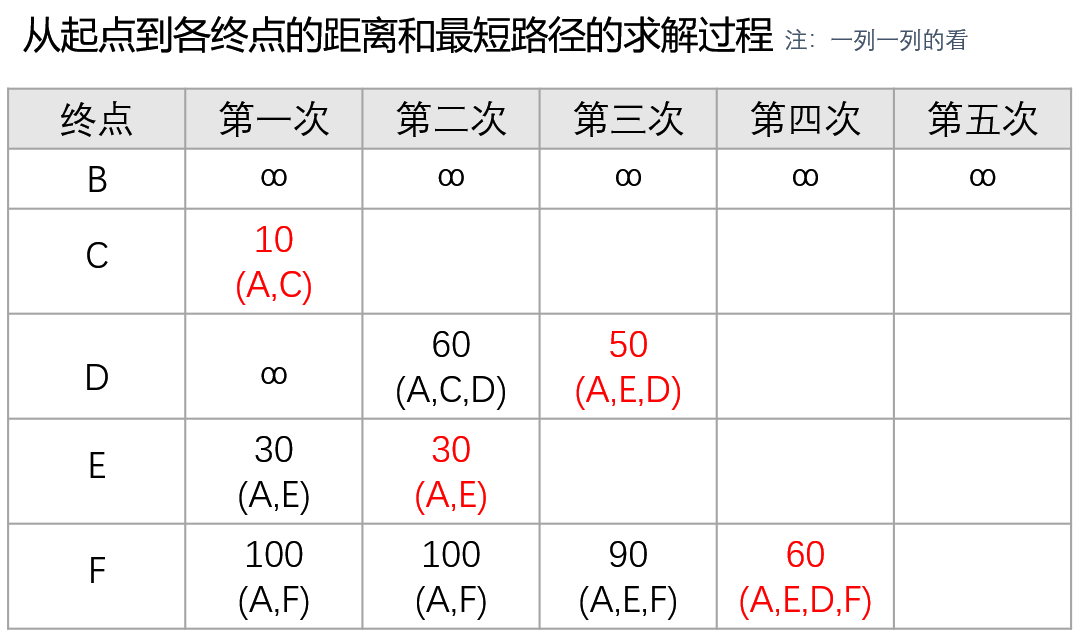
Dijkstra算法求单源最短路径(有向网)
Dijkstra函数:
1 //Dist[MAXVEX],各顶点最短路径长度 2 //Path[MAXVEX][MAXVEX],若Path[i][j] = 1, 则 j 是从源点到 i 间最短路径上的顶点 3 void Dijkstra(AdjMatrix* G, int start, int Dist[], int Path[][MAXVEX]) 4 { 5 int mindist = 0; 6 int i = 0, j = 0, k = 0, s = 0; 7 int final[MAXVEX] = { 0 }; 8 9 for (i = 0; i < G->vexnum; i++)//初始化最短路径及其权值 10 { 11 final[i] = 0; 12 Dist[i] = G->arcs[start][i]; 13 if (Dist[i] < INFINITY) 14 { 15 Path[i][start] = 1; 16 Path[i][i] = 1; 17 } 18 } 19 Dist[start] = 0; 20 final[start] = 1; 21 22 //开始主循环,每次求得start到某个顶点的最短路径 23 for (i = 1; i < G->vexnum; i++) 24 { 25 mindist = INFINITY; 26 for (j = 0; j < G->vexnum; j++) 27 { 28 if (!final[j]) 29 { 30 if (Dist[j] < mindist)//顶点j离start更近 31 { 32 k = j; 33 mindist = Dist[j]; 34 } 35 } 36 } 37 final[k] = 1; 38 for (j = 0; j < G->vexnum; j++)//更新当前最短路径及距离 39 { 40 if (!final[j] && (mindist + G->arcs[k][j] < Dist[j]))//若顶点k的最短路径距离 + k 到 j 的距离 < j 的原来最短路径距离 41 { 42 Dist[j] = mindist + G->arcs[k][j]; 43 for (s = 0; s < G->vexnum; s++)// j 的最短路径 = k 的最短路径 + k 顶点 44 { 45 Path[j][s] = Path[k][s]; 46 } 47 Path[j][j] = 1; 48 } 49 } 50 } 51 }
源代码:

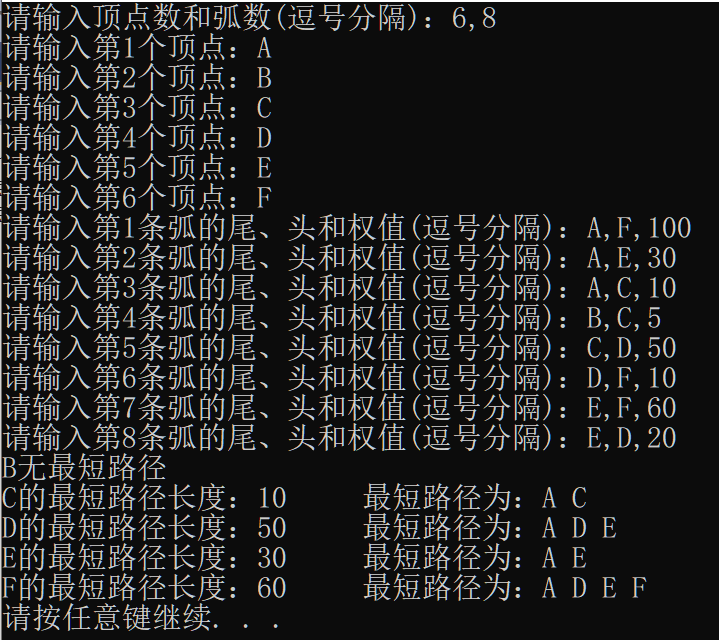
1 #define _CRT_SECURE_NO_WARNINGS 2 #include <stdio.h> 3 #include <stdlib.h> 4 #define MAXVEX 20 5 #define INFINITY 32767 6 7 typedef struct 8 { 9 int vexnum, arcnum; 10 char vex[MAXVEX]; 11 int arcs[MAXVEX][MAXVEX]; 12 }AdjMatrix;//邻接矩阵 13 14 //Dist[MAXVEX],各顶点最短路径长度 15 //Path[MAXVEX][MAXVEX],若Path[i][j] = 1, 则 j 是从源点到 i 间最短路径上的顶点 16 void Dijkstra(AdjMatrix* G, int start, int Dist[], int Path[][MAXVEX]) 17 { 18 int mindist = 0; 19 int i = 0, j = 0, k = 0, s = 0; 20 int final[MAXVEX] = { 0 }; 21 22 for (i = 0; i < G->vexnum; i++)//初始化最短路径及其权值 23 { 24 final[i] = 0; 25 Dist[i] = G->arcs[start][i]; 26 if (Dist[i] < INFINITY) 27 { 28 Path[i][start] = 1; 29 Path[i][i] = 1; 30 } 31 } 32 Dist[start] = 0; 33 final[start] = 1; 34 35 //开始主循环,每次求得start到某个顶点的最短路径 36 for (i = 1; i < G->vexnum; i++) 37 { 38 mindist = INFINITY; 39 for (j = 0; j < G->vexnum; j++) 40 { 41 if (!final[j]) 42 { 43 if (Dist[j] < mindist)//顶点j离start更近 44 { 45 k = j; 46 mindist = Dist[j]; 47 } 48 } 49 } 50 final[k] = 1; 51 for (j = 0; j < G->vexnum; j++)//更新当前最短路径及距离 52 { 53 if (!final[j] && (mindist + G->arcs[k][j] < Dist[j]))//若顶点k的最短路径距离 + k 到 j 的距离 < j 的原来最短路径距离 54 { 55 Dist[j] = mindist + G->arcs[k][j]; 56 for (s = 0; s < G->vexnum; s++)// j 的最短路径 = k 的最短路径 + k 顶点 57 { 58 Path[j][s] = Path[k][s]; 59 } 60 Path[j][j] = 1; 61 } 62 } 63 } 64 } 65 66 int LocateVex(AdjMatrix* G, char vex) 67 { 68 int i = 0; 69 for (i = 0; i < G->vexnum; i++) 70 { 71 if (G->vex[i] == vex) 72 { 73 return i; 74 } 75 } 76 return -1; 77 } 78 79 void Create(AdjMatrix* G) 80 { 81 int i = 0, j = 0, k = 0; 82 int weight = 0; 83 char vex1 = '\0', vex2 = '\0'; 84 85 printf("请输入顶点数和弧数(逗号分隔):"); 86 scanf("%d%*c%d", &G->vexnum, &G->arcnum); 87 88 for (i = 0; i < G->vexnum; i++)//弧初始化 89 { 90 for (j = 0; j < G->vexnum; j++) 91 { 92 G->arcs[i][j] = INFINITY; 93 } 94 } 95 for (i = 0; i < G->vexnum; i++) 96 { 97 printf("请输入第%d个顶点:", i + 1); 98 scanf(" %c", &G->vex[i]); 99 } 100 for (k = 0; k < G->arcnum; k++) 101 { 102 printf("请输入第%d条弧的尾、头和权值(逗号分隔):", k + 1); 103 scanf(" %c%*c%c%*c%d", &vex1, &vex2, &weight); 104 i = LocateVex(G, vex1); 105 j = LocateVex(G, vex2); 106 G->arcs[i][j] = weight; 107 } 108 } 109 110 void Print(AdjMatrix* G, int Dist[], int Path[][MAXVEX]) 111 { 112 int i = 0, j = 0; 113 for (i = 1; i < G->vexnum; i++) 114 { 115 if (Dist[i] == INFINITY) 116 { 117 printf("%c无最短路径\n", G->vex[i]); 118 continue; 119 } 120 else 121 { 122 printf("%c的最短路径长度:%d\t", G->vex[i], Dist[i]); 123 printf("最短路径为:"); 124 } 125 for (j = 0; j < G->vexnum; j++) 126 { 127 if (Path[i][j]) 128 { 129 printf("%c ", G->vex[j]); 130 } 131 } 132 printf("\n"); 133 } 134 } 135 136 int main(void) 137 { 138 AdjMatrix G; 139 int Dist[MAXVEX] = { 0 };//各顶点最短路径长度 140 int Path[MAXVEX][MAXVEX] = { 0 };//若Path[i][j] = 1, 则 j 是从源点到 i 间最短路径上的顶点 141 Create(&G); 142 Dijkstra(&G, 0, Dist, Path); 143 Print(&G, Dist, Path); 144 system("Pause"); 145 return 0; 146 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号