统计学习方法—概论
统计学习方法
实现步骤

主要组成
1. 监督学习
2. 非监督学习
3. 半监督学习
4. 强化学习
监督学习
任务
- 学习一个模型,使模型能够对任意给定的输入,对其相应的输出做一个好的预测
基本概念
- 实例instance
每一个具体的输入是一个实例
通常由特征向量表示,所有特征向量存在的空间——特征空间,特征空间的每一维对应一个特征- 输入实例\(x\)的特征向量记作\(x=(x^{(1)},(x^{(2)},\cdots,(x^{(n)})^{T}\)
- \(x^{(i)}\)表示\(x\)的第\(i\)个特征
- 训练数据集、测试数据
监督学习从训练数据集合中学习模型,然后对测试数据进行预测- 由输入与输出对组成,通常表示为\(T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\)
输入与输出对又称——样本/样本点
- 由输入与输出对组成,通常表示为\(T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\)
- 预测任务分类
基于输入、输出变量的不同类型- 回归问题
- 输入、输出变量均为连续变量
- 分类问题
- 输出变量为有限个离散变量
- 标注问题
- 输入、输出变量均为变量序列
- 假设空间
- 模型属于由输入空间到输出空间的映射的集合,这个集合即为假设空间
- 回归问题
问题的形式化——监督学习问题
- 监督学习分为学习和预测两个过程
![]()
- 给定
- 一个训练数据集\(T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\)
- \(x_i\in \mathcal{X}\in R^n\)为输入的观测值,也称输入/实例
- \(y_i\in \mathcal{Y}\)输出的观测值,也称为输出
- 学习过程
- 学习系统利用给定的训练数据集T
- 通过学习得到一个模型
- 表示为条件概率分布\(\hat{P}(Y|X)\)或决策函数\(Y=\hat{f}(X)\)
- 预测过程
- 预测系统对于给定的测试样本集中的输入\(x_{N+1}\)
- 由模型\(y_{N+1}=\arg \mathop{max}\limits_{y_{N+1}}\hat{P}(y_{N+1}\mid x_{N+1})\)或\(y_{N+1}=\hat{f}(x_{N+1})\)给出相应的输出\(y_{N+1}\)
统计学习三要素
1. 模型
- 假设空间\(\mathcal{F}\)定义
-
决策函数的集合\(\mathcal{F}=\{f\mid Y=f(X)\}\)
非概率模型- X和Y是定义在输入空间\(\mathcal{X}\)和输出空间\(\mathcal{Y}\)上的变量
- 此时\(\mathcal{F}\)通常是由一个参数向量\(\theta\) 决定的函数族\(\mathcal{F}=\{f\mid Y=f_{\theta}(X),\theta\in\mathbf{R}^{n}\}\)
-
条件概率的集合\(\mathcal{F}=\{P\mid P(Y\mid X)\}\)
概率模型- 此时\(\mathcal{F}\)通常是由一个参数向量\(\theta\) 决定的条件概率分布族\(\mathcal{F}=\{P\mid P_{\theta}(Y\mid X),\theta\in\mathbf{R}^{n}\}\)
-
2. 策略
2.1. 损失函数
度量预测错误的程度, 损失函数值越小,模型就越好
-
0-1损失函数
\(L(Y,f(X))=\begin{cases}1,&Y\neq f(X)\\0,&Y=f(X)\end{cases}\) -
平方损失函数
$ L(Y,f(X))=(Y-f(X))^{2}$ -
绝对损失函数
\(L(Y,f(X))=|Y-f(X)|\) -
对数损失函数
\(L(Y,P(Y\mid X))=-\log P(Y\mid X)\)
2.2 期望风险
- 损失函数的期望(模型f(X)关于联合分布P(X,Y)的平均意义下的损失)
- \(R_{\exp}(f)=E_{P}[L(Y,f(X))]=\int_{\mathcal{X}\times \mathcal{Y}}L(y,f(x))P(x,y)\mathrm{d}x\mathrm{d}y\)
- 学习的目标就是选择期望风险\(R_{\exp}(f)\)最小的模型
2.3 经验风险
- 给定一个训练数据集\(T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\)
- 模型\(f(X)\)关于训练数据集的平均损失,记作经验风险\(R_{emp}(f)\)
- \(R_{\mathrm{emp}}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))\)
- 根据大数定律,样本容量N趋向无穷时,经验风险\(R_{emp}(f)\)趋于期望风险\(R_{\exp}(f)\)
2.4 结构风险
- $ R_{\mathrm{srm}}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))+\lambda J(f)$
- \(J(f)\)为模型的复杂度,是定义在假设空间\(\mathcal{F}\)上的泛函,模型\(f\)越复杂,\(J(f)\)越大
泛函——从函数空间到数域的映射 - \(\lambda \ge 0\)是系数,用于权衡经验风险和模型复杂度
2.5 经验风险最小化 ERM
认为经验风险最小的模型为最优模型
-
\(\mathop{min}\limits_{f\in\mathcal{F}} \frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))\)
-
存在问题
- 样本容量很小时,学习效果未必好,会产生过拟合(over-fitting)现象
-
例子
- 极大似然估计: 模型是条件概率分布,损失函数为对数损失函数
2.6 结构风险最小化 SRM
认为结构风险最小的模型为最优模型
防止过拟合提出,SRM等价于正则化
- 结构风险最小的模型往往对训练数据以及未知的测试数据都有较好的预测
- \(\mathop{min}\limits_{f\in\mathcal{F}} \frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))+\lambda J(f)\)
- 例子
- 最大后验概率估计: 模型是条件概率分布,损失函数为对数损失函数,模型复杂度由模型的先验概率表示
3. 算法
指学习模型的具体计算方法,求解最优化问题
模型评估、模型选择
1. 训练误差、测试误差
统计学习的目的是使学到的模型不仅对已知数据而且对未知数据都能有很好的预测能力
1.1 训练误差
- 模型\(Y=\hat{f}(X)\)关于训练数据集的平均损失
- \(R_{\mathrm{emp}}(\hat{f})=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},\hat{f}(x_{i}))\)
- N为训练样本容量
1.2 测试误差
-
模型\(Y=\hat{f}(X)\)关于测试数据集的平均损失
-
\(e_{\mathrm{test}}=\frac{1}{N^{\prime}}\sum_{i=1}^{N^{\prime}}L(y_{i},\hat{f}(x_{i}))\)
-
\(N^{\prime}\)为测试样本容量
-
测试误差反映了学习方法对未知的测试数据集的预测能力,称为泛化能力
- 例如
-
当损失函数为0-1损失时,测试误差\(\rightarrow\)常见的测试数据集上的误差率
\(e_{\mathrm{test}}=\frac{1}{N^{\prime}}\sum_{i=1}^{N^{\prime}}I(y_{i} \neq \hat{f}(x_{i}))\)I为指示函数 -
常见的测试数据集上的准确率
\(r_{\mathrm{test}}=\frac{1}{N^{\prime}}\sum_{i=1}^{N^{\prime}}I(y_{i} = \hat{f}(x_{i}))\)
-
- 例如
2. 过拟合、模型选择
2.1 模型选择
- 当假设空间含有不同复杂度(例如,不同的参数个数)的模型时,就要面临模型选择(model selection)的问题
- 如果在假设空间中存在“真”模型,那么所选择的模型应该逼近真模型。具体地,所选择的模型要与真模型的参数个数相同,所选择的模型的参数向量与真模型的参数向量相近。
2.2 过拟合
- 是指学习时选择的模型包含的参数过多,以至于出现——这一模型对已知数据预测得很好,但对未知数据预测得很差
2.3 训练误差和测试误差与模型的复杂度之间的关系
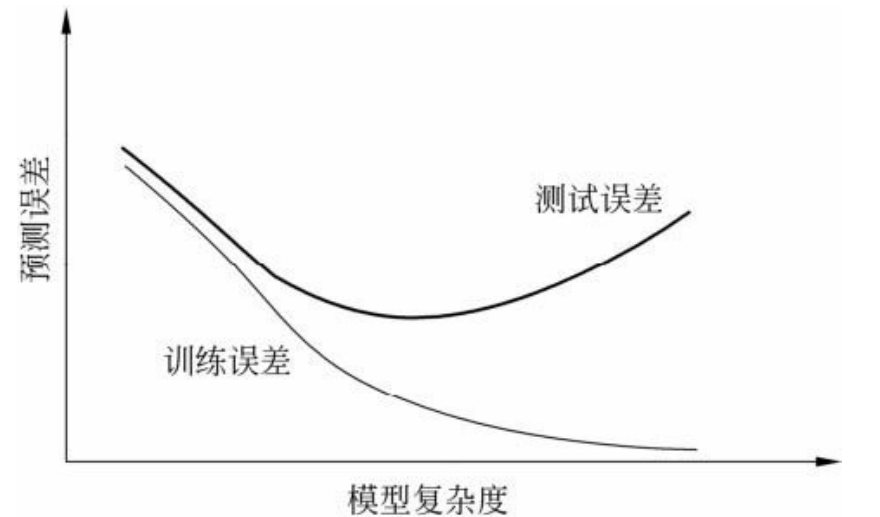
当模型的复杂度增大时,训练误差会逐渐减小并趋向于0;而测试误差会先减小,达到最小值后又增大。
当选择的模型复杂度过大时,过拟合现象就会发生。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号