abc420_e Reachability Query 题解

题目描述：

https://atcoder.jp/contests/abc420/tasks/abc420_e

题目分析：

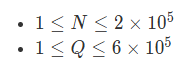
首先观察数据范围，发现N，Q都是10^5级别的，这意味着我们需要复杂度为 O(logN * Q)的方法

分析题目给的三种查询

首先看查询 3 ，唯一包含输出的查询

查询 3 : 判断是否可以通过遍历零条或多条边从顶点 v 到达一个黑色顶点

为回答这个问题，我们必须维护各个节点间的连通性，在节点 v 所在的联通块内寻找有无黑色顶点

注意到题目没有撤销边的操作，也就是说，联通块的大小是只增不减的

考虑使用并查集，维护哪些节点在一个连通块内，并用辅助数组维护一个连通块内黑色节点的数量

这时操作 1 和操作 2 就很容易实现了

操作 1 ：添加一条连接顶点 u 和 v 的无向边
操作 2 : 如果顶点 v 是白色，将其变为黑色；如果是黑色，将其变为白色

对于操作 1 ，只需最基础的合并 O(logn)
对于操作 2 ，只需更改其属于的连通块的黑色节点数量 O(logn)

考虑用cnt[i]来表示该连通块内黑色节点的数量

为简化，每个连通块只维护祖先的值，具体见代码实现

（三种操作复杂度都是logn，总复杂度 O(logN * Q)）

#include <iostream>
#define int long long
using namespace std;
const int MAXN=2e5+7;
int f[MAXN];//并查集
int find(int x){
	if(f[x]==x){
		return x;
	}else{
		return f[x]=find(f[x]);
	}
}
int cnt[MAXN];//连通块的权值
int color[MAXN];//颜色  0/1 --> 白/黑
signed main(){
	int n,q;
	cin>>n>>q;
	for(int i=1;i<=n;i++){
		f[i]=i;//初始化
	}
	for(int i=1;i<=q;i++){
		int opt,u,v;
		cin>>opt;
		if(opt==1){
			cin>>u>>v;
			if(find(u)==find(v)){
				continue;//如果已经在一个连通块内，则无需操作
			}
			cnt[find(v)]+=cnt[find(u)];//find(v)为更新后的总祖先，累加u所在连通块的黑色数量
			cnt[find(u)]=0;//保险清0
			f[find(u)]=find(v);//合并
		}else if(opt==2){
			cin>>v;
			color[v]=(color[v]+1)%2;//更改颜色
			int delta=(color[v]==1?1:-1);//对cnt产生的贡献
			cnt[find(v)]+=delta;
		}else{
			cin>>v;
			if(cnt[find(v)]==0){//没有黑色节点在内
				cout<<"No"<<endl;
			}else{
				cout<<"Yes"<<endl;
			}
		}
	}
}

完结撒花