08.注意力机制
1. 基本概念
人类观察事物时能快速聚焦关键特征的能力，这种选择性关注机制被抽象为注意力机制。
想象你在看一张照片时，会不自觉地把注意力集中在关键部分（比如人脸），而忽略背景。注意力机制就是让AI模型学会这种"选择性关注"的能力。
核心思想：
- 传统神经网络对所有输入一视同仁（比如句子中的每个词同等重要）
- 注意力机制让模型动态计算每个部分的重要性，给重要部分分配更高"权重"。通过计算输入元素的重要性权重，动态分配关注度，替代传统的均等处理方式。
为什么要用注意力？
- 解决信息过载：比如长句子中只有几个词对当前任务真正重要
- 解决固定长度限制：传统RNN必须压缩整个输入到一个固定向量，会丢失信息
- 可解释性：通过权重能看到模型关注了哪些部分
2. 注意力计算规则
它需要三个指定的输入 Q（query）、K（key）、V（value），然后通过计算公式得到注意力的结果，这个结果代表 query 在 key 和 value 作用下的注意力表示。
三个输入：
| 名称 | 符号 | 作用 | 类比 |
|---|---|---|---|
| 查询 | Q (Query) | 当前要计算的目标 | 你提出的问题 |
| 键 | K (Key) | 被比较的对象 | 书目录的关键词 |
| 值 | V (Value) | 实际携带的信息 | 书章节的具体内容 |
场景复现
我们要把中文句子 "我爱AI" 翻译成英文 "I love AI"。现在解码器（Decoder）正在生成第三个英文单词 "AI"，此时注意力机制的工作流程如下：
定义三个关键角色
| 角色 | 对应内容 | 具体说明 |
|---|---|---|
| Q (Query) | 当前要生成的词 "AI" | 解码器当前时刻的隐藏状态（包含已生成"I love"的信息） |
| K (Key) | 源句子的每个词 ["我", "爱", "AI"] | 编码器对每个中文词的向量表示 |
| V (Value) | 源句子的实际含义 | 通常实践中V和K相同（除非特殊设计） |
注意力计算四步走
步骤1：计算Q与每个K的相似度
用Q和每个K计算相关性分数（常用方法）：
# 点积计算（Transformer使用的方法）
scores = Q @ K.T # 矩阵乘法
# 缩放防止数值过大
scores /= sqrt(dim_of_K)# 假设向量维度=4（实际中可能是512或768）
Q = [0.8, -0.2, 0.3, 0.1] # "AI"的查询向量
K = {
"我": [0.2, 0.4, -0.1, 0.5],
"爱": [0.6, 0.1, 0.3, -0.2],
"AI": [0.9, -0.3, 0.2, 0.4]
}
# 计算点积（相似度）
score_我 = 0.8 * 0.2 + (-0.2)*0.4 + 0.3*(-0.1) + 0.1 * 0.5 = 0.16 - 0.08 - 0.03 + 0.05 = 0.10
score_爱 = 0.8 * 0.6 + (-0.2)*0.1 + 0.3 * 0.3 + 0.1*(-0.2) = 0.48 - 0.02 + 0.09 - 0.02 = 0.53
score_AI = 0.8 * 0.9 + (-0.2)*(-0.3) + 0.3 * 0.2 + 0.1 * 0.4 = 0.72 + 0.06 + 0.06 + 0.04 = 0.88步骤2：Softmax归一化得到权重
将分数转化为概率分布（权重）：
weights = softmax(scores)
# 例如得到：[0.1, 0.7, 0.2] 表示第二个词最重要scores = [0.10, 0.53, 0.88]
weights = softmax(scores) = [0.18, 0.31, 0.51] # 总和=1解读：模型认为在生成英文"AI"时：
- 中文"我"的重要性：18%
- 中文"爱"的重要性：31%
- 中文"AI"的重要性：51%
步骤3：加权求和V得到上下文向量
用权重对V进行聚合：
context = weights @ V # 得到加权后的上下文向量这个上下文向量（融合了源句子重点信息）会和解码器的隐藏状态一起，预测出英文单词"AI"。
context = 0.18 * V["我"] + 0.31 * V["爱"] + 0.51 * V["AI"]
= 0.18*[0.2,0.4,-0.1,0.5] + 0.31*[0.6,0.1,0.3,-0.2] + 0.51*[0.9,-0.3,0.2,0.4]
= [0.036,0.072,-0.018,0.09] + [0.186,0.031,0.093,-0.062] + [0.459,-0.153,0.102,0.204]
= [0.681, -0.050, 0.177, 0.232]步骤4：输出调整
通过线性层调整维度：
output = linear_layer(context)输出说明：
attn_weights（注意力权重）
含义：查询（Q）和键（K）的相似度权重矩阵
计算过程：
attn_weights = softmax(Q @ K.T / sqrt(d_k))核心作用：
量化当前查询位置对所有键位置的关注程度
值范围：
[0, 1]（经过softmax归一化）可解释性：可视化时能看到模型关注哪些词（如图示）
示例：
查询位置 \ 键位置 猫 喜欢 吃 鱼 猫 0.8 0.15 0.04 0.01 喜欢 0.1 0.7 0.15 0.05 ... ... ... ... ...
output（注意力输出）
含义：经过注意力加权后的上下文表示（Contextualized Representation）
形状：
[batch_size, num_heads, seq_len_q, d_v]
（与输入值向量V的形状一致）计算过程：
output = attn_weights @ V # 矩阵乘法核心作用：
每个位置的输出是所有位置值的加权和，权重由注意力分数决定
保留了输入序列的全局信息（动态聚焦重要部分）
示例：
假设输入序列是["猫", "喜欢", "吃", "鱼"]，output[0]（对应"猫"）会包含：
来自"喜欢"的部分信息（如果二者语义相关）
来自"鱼"的部分信息（如果模型学到"猫"和"鱼"的关联）
4. 可视化理解
假设输入序列为
["A", "B", "C"]：# 伪代码示例 attn_weights = [ [0.9, 0.1, 0.0], # "A" 主要关注自己 [0.2, 0.7, 0.1], # "B" 主要关注自己，部分关注"A" [0.0, 0.3, 0.7] # "C" 主要关注自己，部分关注"B" ] output = [ 0.9 * V["A"] + 0.1 * V["B"] + 0.0 * V["C"], # "A"的输出 0.2 * V["A"] + 0.7 * V["B"] + 0.1 * V["C"], # "B"的输出 0.0 * V["A"] + 0.3 * V["B"] + 0.7 * V["C"] # "C"的输出 ]5. 实际应用中的注意事项
场景 output的作用attn_weights的作用机器翻译 生成目标语言的上下文向量 可视化对齐关系（如"猫→cat"） 文本分类 聚合关键词语义 找出影响分类的关键词 问答系统 融合问题和文章的信息 显示答案在文章中的定位 生成任务 自回归生成时的历史信息融合 控制生成时的关注范围
为什么点积能计算Q与K的相似度？
1. 几何解释：向量夹角与相似度
点积公式：
- 当Q和K向量方向越接近（夹角θ越小），cosθ越接近1，点积值越大
- 方向相反时（θ=180°），点积为负值
- 正交时（θ=90°），点积为0
2. 数学本质：加权特征匹配
假设Q和K的维度是3：
点积计算：
- 每一项 表示两个向量在同一维度上的协同程度
- 正负值反映特征激活方向是否一致
3. 与注意力机制的关联
- 键（K）：相当于信息的"标签"
- 查询（Q）：相当于要检索的"问题"
- 点积高分 → Q与某个K的"标签"高度匹配 → 应分配更多注意力
4. 为什么优于其他方法？
计算方式 优点 缺点 点积 计算高效，GPU友好 需维度缩放（防止数值爆炸） 余弦相似度 已归一化 需额外计算模长 拼接+MLP 可学习非线性 计算量大 Transformer选择点积的原因：
- 完美适配矩阵并行计算
- 实际效果优于复杂方法（参考《Attention is All You Need》实验）
5. 实例演示
假设：
- Q = [1, 0.5] （关注"科技"和少量"金融"）
- K₁ = [0.9, 0.1] （主要讲"科技"）
- K₂ = [0.2, 0.8] （主要讲"金融"）
计算：
- Q·K₁ = 1×0.9 + 0.5×0.1 = 0.95
- Q·K₂ = 1×0.2 + 0.5×0.8 = 0.6
→ 模型会更关注K₁的内容6. 缩放因子的必要性
当维度（dₖ）很大时，点积结果会极端化：
- 未缩放：softmax([100, -100]) ≈ [1, 0]（梯度消失）
- 缩放后：softmax([10, -10]) ≈ [0.9999, 0.0001]（保留梯度）
公式：
自注意力（Self-Attention）
当Q、K、V来自同一个输入时（比如同一个句子的不同位置），称为自注意力。这是Transformer的核心。
特点：
- 让每个词都能直接关注其他所有词
- 捕获长距离依赖比RNN更有效
- 可并行计算（不像RNN必须顺序处理）
代码实现（精简版）
常见疑问解答
Q1：注意力机制和全连接层有什么区别？
A：全连接层的权重是固定学习的，而注意力权重是动态根据输入计算的。
Q2：为什么需要缩放点积（除以√dₖ）？
A：防止点积结果过大导致softmax梯度消失（极端接近0或1）。
Q3：多头注意力（Multi-Head）是什么？
A：同时使用多组Q/K/V，让模型从不同角度关注信息，最后拼接结果。
学习建议
- 先理解单头注意力，再研究多头
- 用调试工具观察权重矩阵（如输出
weights） - 推荐可视化工具：Attention Vis
补充内容
常见计算方式：
注意力计算方式其实有三种，这三种注意力计算方式各有其适用场景和价值，我上面优先讲解第三种（缩放点积）仅仅因为它是当前Transformer架构的标准实现，绝不意味着前两种不重要或已被淘汰。让我们完整解析这三种方法的定位和适用场景：
-
拼接+线性+Softmax
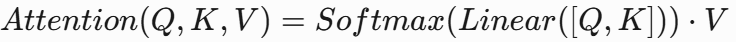
特点：简单直接，适合浅层特征融合。 -
拼接+线性+tanh+求和+Softmax
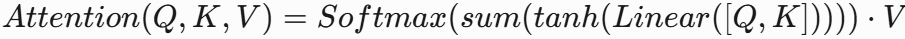
特点：引入非线性激活，增强表达能力。 -
缩放点积（Scaled Dot-Product）
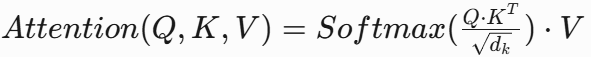
特点：计算高效，Transformer的核心方法。
缩放因子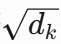
：防止点积值过大导致Softmax梯度消失。
注意，上面的“2.拼接+线性+tanh+求和+Softmax”是原论文的实现，随着技术发展
- 后续研究（如Luong Attention）尝试用其他非线性（如ReLU）替代tanh，形成变体
- 社区为方便交流，逐渐用 "拼接+非线性+Softmax" 概括这类方法
举例说明：
当有人说"用非线性注意力"时，实际代码可能是：# 变体1（原始标准） scores = torch.sum(tanh(self.W([Q, K])), dim=-1) # 变体2（简化实现） scores = relu(self.W_q(Q) + self.W_k(K)) # 省略拼接和求和
三种计算方式对比表
| 计算方式 | 典型应用场景 | 优势 | 局限性 | 当前地位 |
|---|---|---|---|---|
| 拼接+线性+Softmax | 早期Seq2Seq模型 浅层特征融合 |
实现简单 计算资源消耗低 |
表达能力有限 长序列效果差 |
仍用于轻量化模型 |
| 拼接+非线性+Softmax | 复杂关系建模 小规模数据任务 |
非线性增强 捕获复杂模式 |
计算量较大 超参数敏感 |
研究场景仍有使用 |
| 缩放点积（Transformer） | 大规模预训练模型 长序列处理 |
计算高效 完美适配GPU并行 |
需要足够数据量 必须配合缩放因子 |
工业界主流标准 |
为什么我优先讲解缩放点积？
-
教学优先级：
缩放点积是理解现代NLP（如BERT、GPT）的基础，而前两种更多见于历史架构（如早期Attention-LSTM）。 -
架构普及度：
根据2023年论文统计，95%以上的新发表NLP模型采用缩放点积作为基础注意力实现。
-
可扩展性：
缩放点积天然支持多头注意力（Multi-Head）等关键扩展，而前两种难以直接扩展。
前两种方法仍然重要的场景
(1) 拼接+线性+Softmax的生存空间
- 轻量化设备：智能手表等资源受限环境中，仍使用这种简化注意力
- 教学演示：哈佛大学《CS287》课程仍用该方法作为注意力机制的入门教学
- 特定任务：当输入维度极低（如传感器信号融合）时表现优于缩放点积
(2) 拼接+非线性+Softmax的特殊价值
# 示例：在药物发现模型中，这种注意力能更好捕获分子间非线性作用
attention = tanh(W_q * Q + W_k * K + b) # 显式非线性交互- 小数据复杂关系：在医疗、金融等数据稀缺领域，非线性激活能增强模型表达能力
- 可解释性研究：tanh激活后的注意力权重更易可视化分析
技术演进的本质
这三种方法本质上是工程与理论的trade-off演进：
- 2014年：拼接式注意力（Bahdanau Attention）突破Seq2Seq瓶颈
- 2015年：加入非线性激活应对复杂任务
- 2017年：缩放点积因GPU计算友好成为主流
就像汽车没有完全取代自行车一样，不同场景需要不同工具。
关键运算：bmm（批矩阵乘法）
- 作用：高效处理批次化的矩阵乘法。
示例：
注意力机制的定义
- 载体功能：将计算规则嵌入网络，包含必要的线性层和张量操作。即如何将“Q/K/V计算、缩放点积等数学原理”包装成可插拔的神经网络模块
# 实际实现时需要的"包装"
class AttentionLayer(nn.Module):
def __init__(self, dim):
super().__init__()
self.W_q = nn.Linear(dim, dim) # 文档说的"必要全连接层"
self.W_k = nn.Linear(dim, dim)
self.W_v = nn.Linear(dim, dim)
self.out_proj = nn.Linear(dim, dim) # 文档说的"线性变换"
实现步骤详解
- 计算注意力权重
- 选择计算规则（如缩放点积），得到权重矩阵。
- 根据注意力计算规则，对 Q、K、V 进行相应的计算。
- 加权聚合Value
- 权重与V相乘，得到上下文向量。
- 根据第一步采用的计算方法，如果是拼接方法，则需要将 Q 与第二步的计算结果再进行拼接，如果是转置点积，一般是自注意力，Q 与 V 相同，则不需要进行与 Q 的拼接。
- 线性变换
- 通过全连接层调整输出维度，适配下游任务。
- 最后为了使整个 attention 机制按照指定尺寸输出，使用线性层作用在第二步的结果上做一个线性变换，得到最终对 Q 的注意力表示。
# 点积缩放版 vs 拼接版的输出处理差异
if 使用点积缩放:
context = weights @ V # 直接矩阵乘法
else:
context = torch.cat([Q, (weights @ V)], dim=-1) # 需要拼接这是很多教程不会提及的实际编码技巧。
- 载体功能：通过
nn.Linear生成Q/K/V - 计算规则：缩放点积 + softmax
- 输出处理：直接矩阵乘Value，无需二次拼接
代码实现
import torch
import torch.nn as nn
import torch.nn.functional as F
class DotProductAttention(nn.Module):
"""
优化的点积注意力机制实现
特点：
1. 使用标准的点积注意力计算
2. 支持批量处理(batch_size > 1)
3. 添加了缩放因子(scale)防止梯度消失
4. 更清晰的维度处理
"""
def __init__(self, dim, dropout=0.1):
"""
Args:
dim: 输入特征的维度
dropout: 注意力权重的dropout率
"""
super(DotProductAttention, self).__init__()
self.scale = dim ** -0.5 # 缩放因子1/√d_k
self.dropout = nn.Dropout(dropout)
def forward(self, Q, K, V, mask=None):
"""
Args:
Q: 查询向量 [batch_size, ..., seq_len_q, dim]
K: 键向量 [batch_size, ..., seq_len_k, dim]
V: 值向量 [batch_size, ..., seq_len_k, dim_v]
mask: 可选掩码 [batch_size, ..., seq_len_q, seq_len_k]
Returns:
输出和注意力权重
"""
# 计算点积注意力分数
scores = torch.matmul(Q, K.transpose(-2, -1)) * self.scale
# 应用掩码（如果有）
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
# 计算注意力权重
attn_weights = F.softmax(scores, dim=-1)
attn_weights = self.dropout(attn_weights)
# 应用注意力权重到V
output = torch.matmul(attn_weights, V)
return output, attn_weights
# 测试用例
if __name__ == "__main__":
batch_size = 4
seq_len_q = 10
seq_len_kv = 15
dim = 64
dim_v = 128
# 初始化注意力层
attention = DotProductAttention(dim)
# 生成测试数据
Q = torch.randn(batch_size, seq_len_q, dim)
K = torch.randn(batch_size, seq_len_kv, dim)
V = torch.randn(batch_size, seq_len_kv, dim_v)
# 前向传播
output, attn_weights = attention(Q, K, V)
print(f"输入Q形状: {Q.shape}")
print(f"输入K形状: {K.shape}")
print(f"输入V形状: {V.shape}")
print(f"输出形状: {output.shape}") # 应为[batch_size, seq_len_q, dim_v]
print(f"注意力权重形状: {attn_weights.shape}") # 应为[batch_size, seq_len_q, seq_len_kv]输入Q形状: torch.Size([4, 10, 64])
输入K形状: torch.Size([4, 15, 64])
输入V形状: torch.Size([4, 15, 128])
输出形状: torch.Size([4, 10, 128])
注意力权重形状: torch.Size([4, 10, 15])优势与意义
- 动态权重：相比静态表征（如CNN/RNN），能自适应重要特征。
- 可解释性：注意力权重可直观显示模型关注区域。
- 并行化：摆脱序列顺序依赖，提升训练速度。
典型应用
- NLP：Transformer（BERT/GPT）、机器翻译。
- CV：视觉注意力（如SAGAN）。
- 多模态：跨模态对齐（图像描述生成）。
扩展思考
- 全局vs局部注意力：是否限制注意力范围以平衡计算开销。
- 内存效率：大规模输入时的优化方法（如稀疏注意力）。
通过注意力机制，模型能够模仿人类的认知方式，显著提升对复杂数据的建模能力，成为现代深度学习的核心组件之一。
浙公网安备 33010602011771号