07.RNN模型简介(传统RNN、LSTM、GRU)
该博客确实缺少近5年(2020-2025)关键进展(如Transformer的对比、现代RNN变种如SRU),但作为基础原理讲解仍然合格。
当前(2025年)工业界的技术采用情况:
- 纯RNN使用率:<15%
- LSTM/GRU使用率:约30%(主要在嵌入式设备)
- Transformer架构:约55%(但其中20%会结合RNN模块)
建议用2-3天掌握该博客内容,然后快速过渡到Transformer学习,但保留这个"技术考古"的认知框架。
学习路线建议:
什么是RNN模型?
- 全称:Recurrent Neural Network(循环神经网络)
- 核心特点:
- 序列数据处理:专为处理时序数据(如语言、语音、时间序列)设计。
- 循环机制:隐层输出会作为下一时间步的输入的一部分,形成信息传递链。
- 动态输入输出:支持变长输入和输出(取决于具体结构类型)。
一般单层神经网络:仅包含 Input→Hidden→Output 的单向传递:
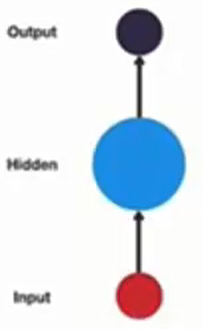
RNN 单层网络:引入 Hidden State,通过时间步展开形成循环结构,实现序列信息的传递:
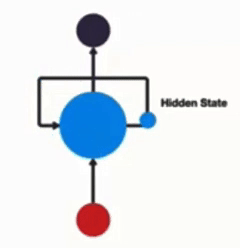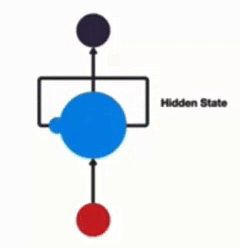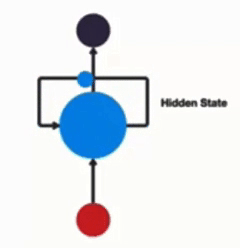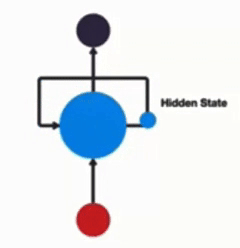
以时间步进行展开后的单层网络结构:

循环机制使隐层上一时间步的输出能作为当下时间步输入的一部分(结合当前输入)影响当前输出,体现了对序列连续性的建模能力。
RNN 模型的作用
- 核心优势:能有效利用序列之间的关系,适合处理具有连续性的输入序列(如人类语言、语音等)。
- 应用场景:广泛应用于 NLP 领域,如文本分类、情感分析、意图识别、机器翻译等。
RNN运行过程示例(用户意图识别)

以输入句子 “What time is it ?” 为例:
![]()
分词:将句子拆分为单词序列,RNN 按顺序逐词处理。
![]()
- 第一步:输入 “What”,产生输出 O1。

- 第二步:输入 “time”,结合上一步隐层输出 O1,产生输出 O2。
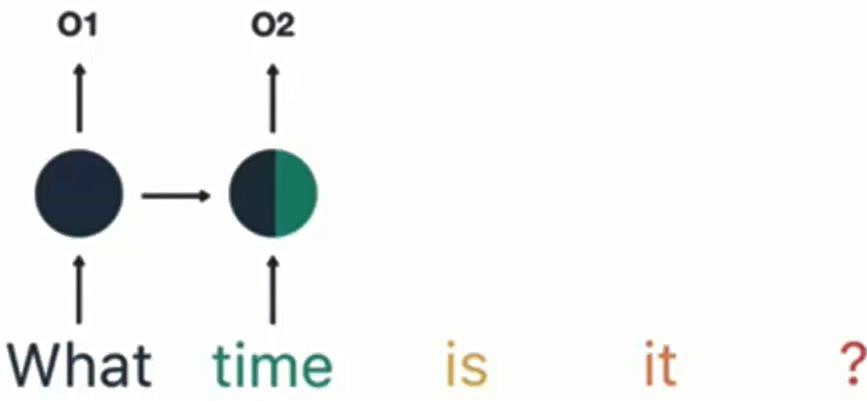
- 后续步骤:重复上述过程,依次处理 “is”“it”“?”,产生 O3、O4、O5。
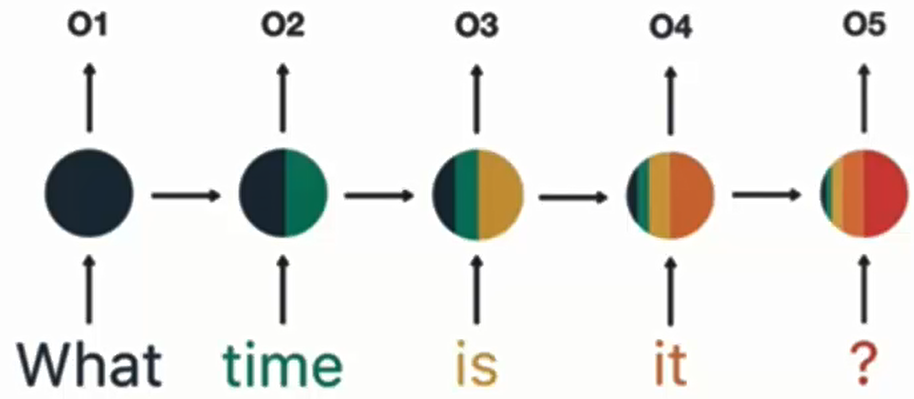
通过最终隐层输出 O5 解析用户意图(如 “询问时间”)。

意图解析:对O5做softmax分类,得到意图标签(如"询问时间")。
RNN 模型的分类
按输入和输出的结构分类
| 类型 | 特点 | 应用场景 |
|---|---|---|
| N vs N | 输入输出序列等长(如输入5词,输出5标签) | 生成等长合辙诗句、序列标注 |
| N vs 1 | 输入序列,输出单个值(最后一个隐层输出经线性变换 + 激活函数处理) | 文本分类、意图识别、情感分析 |
| 1 vs N | 输入单个值(如图像),输出序列(如描述)(输入作用于每次输出) | 图像描述生成(图片生成文字) |
| N vs M | 输入输出不等长,由编码器和解码器组成(seq2seq 架构),通过隐含变量 c 传递信息 | 机器翻译、文本摘要、、阅读理解 |
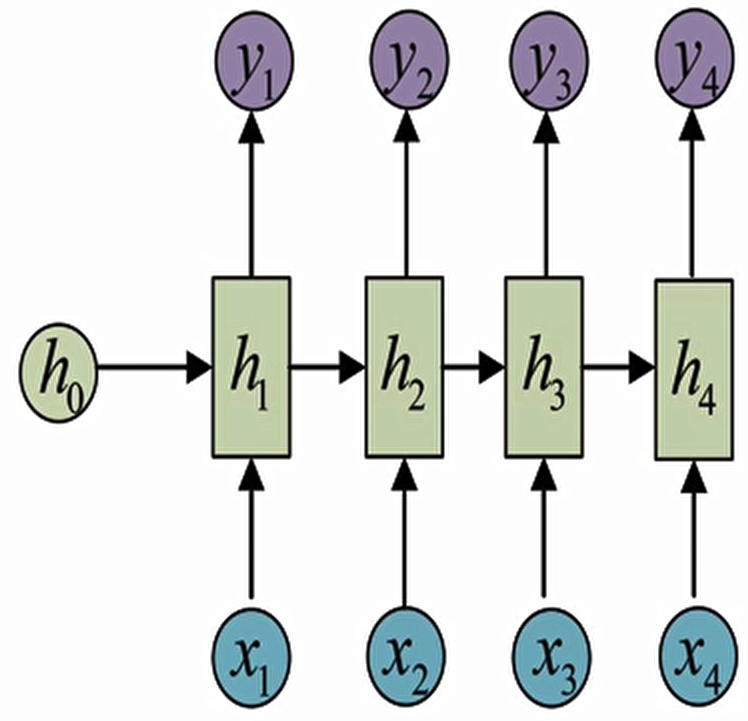
N VS N- RNN:
它是RNN最基础的结构形式,最大的特点就是: 输入和输出序列是等长的.由于这个限制的存在,使其适用范围比较小,可用于生成等长度的合辙诗句.
N VS 1-RNN:
有时候我们要处理的问题输入是一个序列,而要求输出是一个单独的值而不是序列,应该怎样建模呢?我们只要在最后一个隐层输出h上进行线性变换就可以了,大部分情况下为了更好的明确结果,还要使用sigmoid或者softmax进行处理,这种结构经常被应用在文本分类问题上.
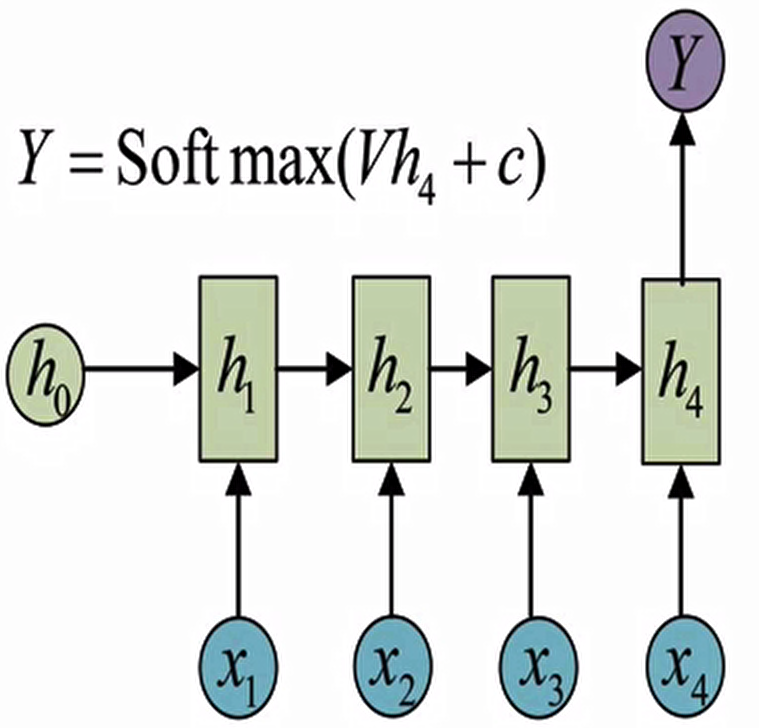
1 VS N - RNN:
如果输入不是序列而输出为序列的情况怎么处理呢?我们最常采用的一种方式就是使该输入作用于每次的输出之上.这种结构可用于将图片生成文字任务等.
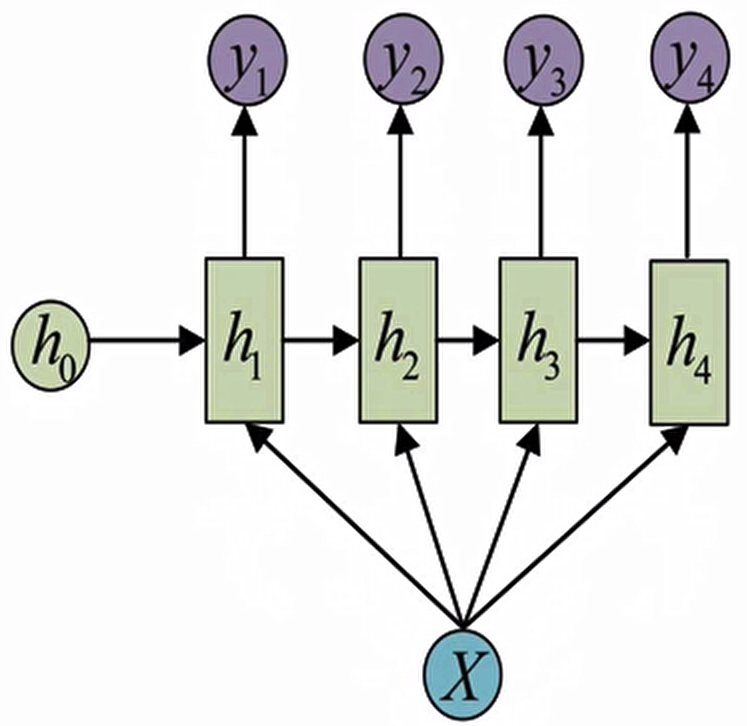
N VS M- RNN:
这是一种不限输入输出长度的RNN结构,它由编码器和解码器两部分组成,两者的内部结构都是某类RNN,它也被称为seq2seq架构.输入数据首先通过编码器,最终输出一个隐含变量c,之后最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上,以保证输入信息被有效利用。
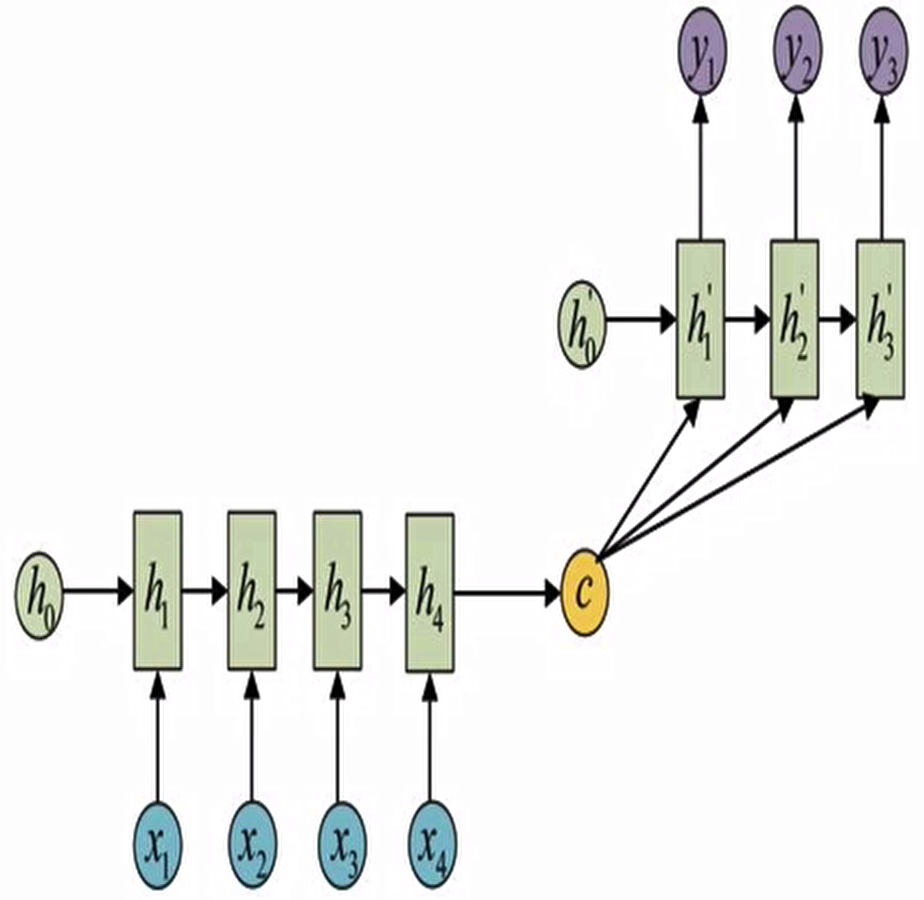
seq2seq架构最早被提出应用于机器翻译,因为其输入输出不受限制,如今也是应用最广的RNN模型结构.在机器翻译,阅读理解,文本摘要等众多领域都进行了非常多的应用实践。
Sequence-to-sequence
Input a sequence, output a sequence.
按内部构造分类
- 基础RNN:简单循环单元,存在梯度消失/爆炸问题。
- LSTM(长短期记忆):
- 引入门控机制(输入门、遗忘门、输出门),缓解长程依赖问题。
- Bi-LSTM:双向处理序列,同时捕捉前后文信息。
- GRU(门控循环单元):
- LSTM的简化版,合并门控结构,计算效率更高。
- Bi-GRU:双向GRU,兼顾前后信息。
通过上述结构,RNN成为处理序列数据的基石模型,后续的LSTM、GRU等改进进一步推动了NLP领域的发展。
小节总结
- RNN 是处理序列数据的循环神经网络,通过循环机制捕捉序列关系,输入输出多为序列形式。
- 其核心作用是建模序列连续性,广泛应用于 NLP 各类任务。
- 按输入输出结构可分为 N vs N、N vs 1、1 vs N、N vs M(seq2seq 架构),按内部构造可分为传统 RNN、LSTM、GRU 及其双向变体等。
- seq2seq 架构因输入输出长度灵活,在机器翻译等领域应用最广。
传统 RNN 模型
学习目标
- 了解传统 RNN 的内部结构及计算公式
- 掌握 Pytorch 中传统 RNN 工具的使用
- 了解传统 RNN 的优势与缺点
传统 RNN 的内部结构图
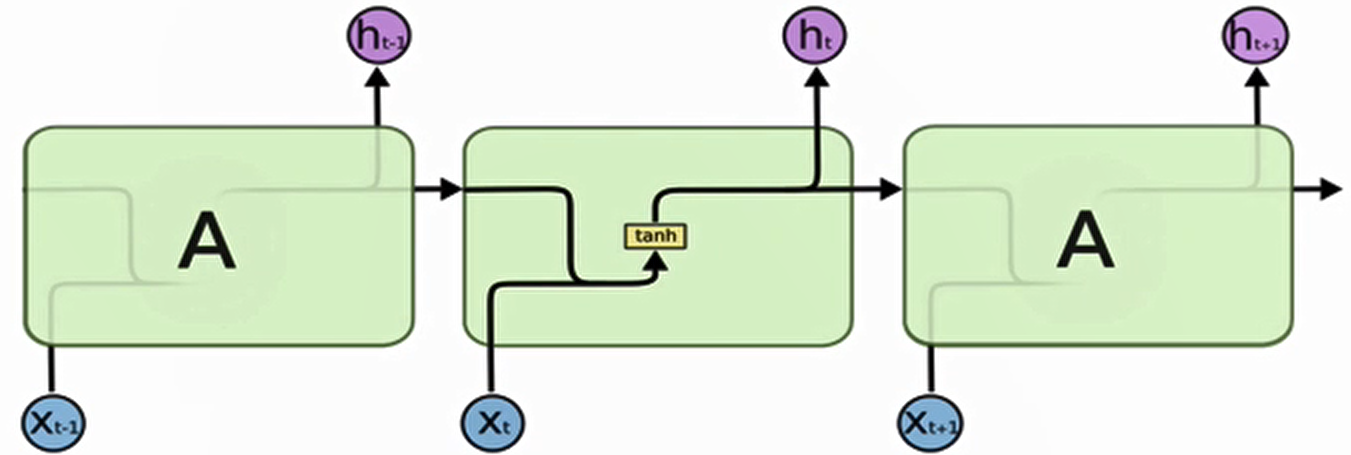
结构解释图

内部结构分析
内部结构过程演示
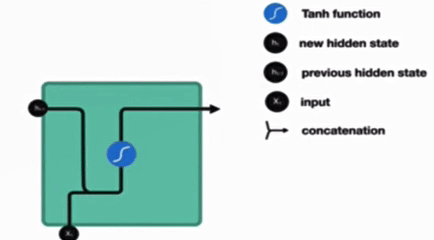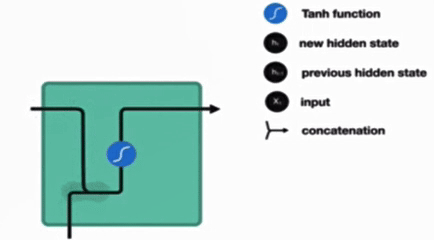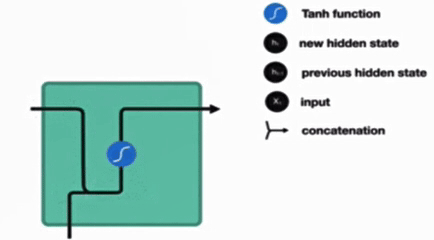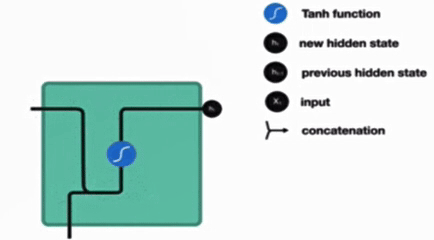
根据结构分析得出内部计算公式
激活函数 tanh 的作用
- 用于帮助调节流经网络的值,tanh 函数将值压缩在 - 1 和 1 之间。
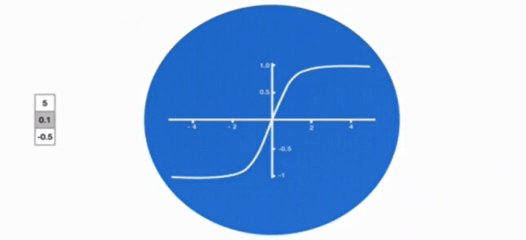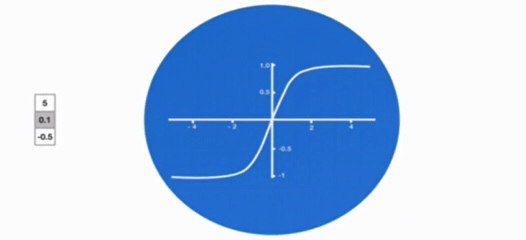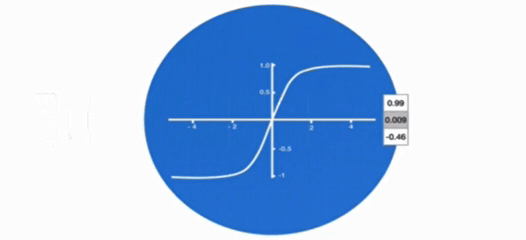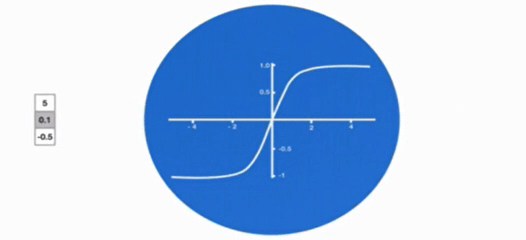
实例演示
假设:
- 当前输入
x_t包含关键词"毕业"(重要事件) - 上一状态
h_{t-1}含有高频记忆"校园" - 模型已学到
W_f会赋予这类组合较高权重
计算过程:
原始决策值 = W_f·["校园","毕业"] + b_f = 1.8
f_t = tanh(1.8) ≈ 0.86 # 模型决定保留86%记忆Pytorch 中传统 RNN 工具的使用
- 位置:在 torch.nn 工具包之中,通过 torch.nn.RNN 可调用。
初始化参数(创建RNN时的配置)
rnn = nn.RNN(input_size=5, hidden_size=6, num_layers=2)| 参数名 | 通俗解释 | 类比说明 |
|---|---|---|
input_size |
每个时间步输入的特征维度 | 如同一个字的"笔画数"(如5笔) |
hidden_size |
隐藏状态的维度(记忆容量) | 如同大脑的"记忆格子数"(6格) |
num_layers |
堆叠的RNN层数 | 如同"大脑的层数"(2层) |
nonlinearity |
激活函数(tanh或relu) |
决定信息如何过滤 |
前向传播参数(调用RNN时的输入)
output, hn = rnn(input, h0)| 参数名 | 形状说明 | 关键作用 | 示例形状 |
|---|---|---|---|
input |
(seq_len, batch, input_size) |
输入序列数据 | (3, 1, 5) |
h0 |
(num_layers, batch, hidden_size) |
初始隐藏状态(记忆起点) | (2, 1, 6) |
具体例子拆解
假设我们要处理一个句子:
- 每个词用5维向量表示(
input_size=5) - 希望RNN记忆容量为6维(
hidden_size=6) - 使用2层RNN(
num_layers=2)
import torch
import torch.nn as nn
# 输入:3个词的句子,batch_size=1
input = torch.randn(3, 1, 5) # 形状 (seq_len=3, batch=1, input_size=5)
# 初始隐藏状态(2层RNN,每层记忆6维)
h0 = torch.zeros(2, 1, 6) # 形状 (num_layers=2, batch=1, hidden_size=6)
rnn = nn.RNN(input_size=5, hidden_size=6, num_layers=2)
output, hn = rnn(input, h0)
print(output)
print(hn)tensor([[[-0.2832, -0.0154, -0.2015, 0.5637, -0.2410, 0.4240]],
[[-0.4879, -0.0030, -0.5890, 0.6971, -0.0303, -0.3094]],
[[-0.3178, -0.1804, -0.1506, 0.6038, 0.0573, 0.1335]]],
grad_fn=<StackBackward0>)
tensor([[[-0.4636, -0.4795, -0.5592, -0.5236, 0.7860, -0.6352]],
[[-0.3178, -0.1804, -0.1506, 0.6038, 0.0573, 0.1335]]],
grad_fn=<StackBackward0>)output形状为(3, 1, 6):每个时间步的输出隐藏状态hn形状为(2, 1, 6):最后一层的最终记忆状态
为什么需要这些参数?
-
input_size:告诉RNN每个时间步吃进去的数据形状
(如同知道每个汉字有多少笔画) -
hidden_size:控制模型的记忆能力
(维度越大能记住的信息越多,但计算量也越大) -
num_layers:增加网络深度,提取更复杂的特征
(如同先理解单字,再理解词语,最后理解句子)
通过这种设计,RNN可以像人阅读一样:
逐时间步处理(读每个词)→ 更新记忆状态(理解上下文)→ 输出结果
传统 RNN 的优缺点
传统 RNN 的优势
- 由于内部结构简单,对计算资源要求低
- 相比之后要学习的RNN变体:LSTM和GRU模型参数总量少了很多
- 在短序列任务上性能和效果都表现优异
传统 RNN 的缺点
- 传统RNN在解决长序列之间的关联时,通过实践,证明经典RNN表现很差
- 原因是在进行反向传播的时候,过长的序列导致梯度的计算异常,发生梯度消失或爆炸
什么是梯度消失或爆炸呢?
梯度消失或爆炸的危害
- 如果在训练过程中发生了梯度消失,权重无法被更新,最终导致训练失败;梯度爆炸所带来的梯度过大,大幅度更新网络参数,在极端情况下,结果会溢出(NaN 值)。
LSTM 模型
学习目标
- 了解 LSTM 内部结构及计算公式
- 掌握 Pytorch 中 LSTM 工具的使用
- 了解 LSTM 的优势与缺点
LSTM 基本概念
LSTM 内部结构及计算公式
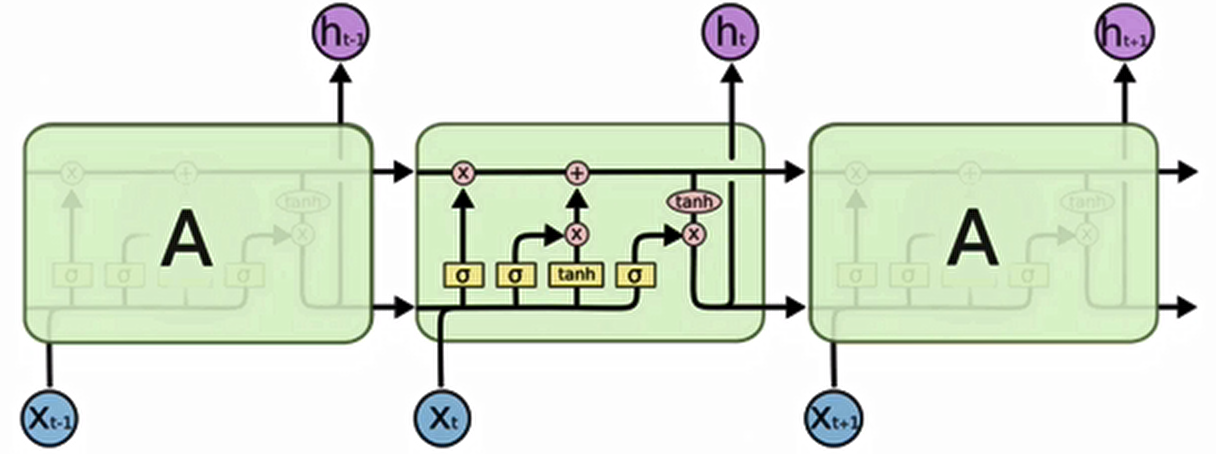

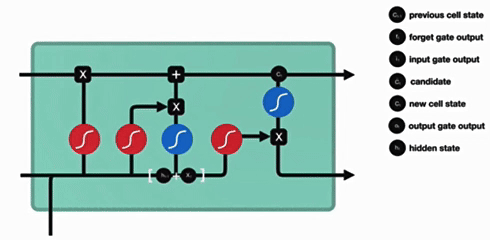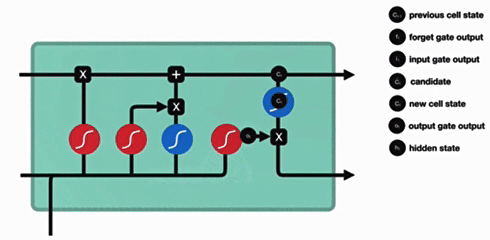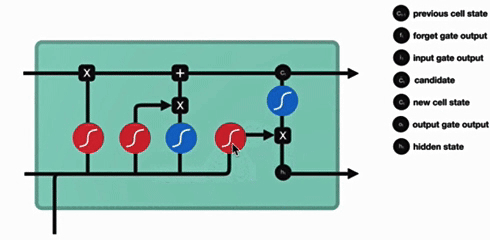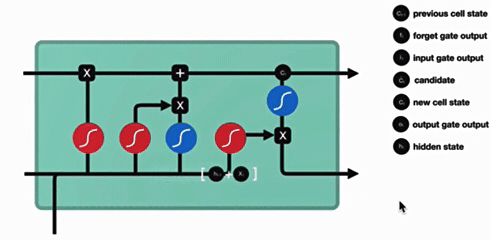
1. 遗忘门
遗忘门结构分析:
与传统RNN的内部结构计算非常相似,首先将当前时间步输入x(t)与上一个时间步隐含状态h(t-1)拼接,得到[x(t),h(t-1)],然后通过一个全连接层做变换,最后通过sigmoid函数进行激活得到f(t),我们可以将f(t)看作是门值,好比一扇门开合的大小程度,门值都将作用在通过该扇门的张量,遗忘门门值将作用的上一层的细胞状态上,代表遗忘过去的多少信息,又因为遗忘门门值是由x(t),h(t-1)计算得来的,因此整个公式意味着根据当前时间步输入和上一个时间步隐含状态h(t-1)来决定遗忘多少上一层的细胞状态所携带的过往信息。
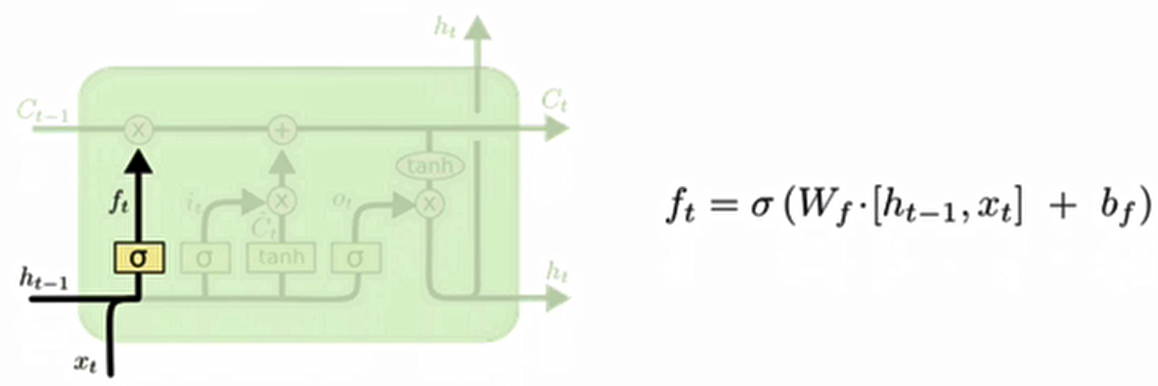
类比解释(先建立直觉)
想象你在决定要忘记多少童年记忆:
-
- σ函数:相当于你的"遗忘开关",但它自己不能做决定,只是把决定压缩到0-1之间(1=完全记住,0=完全忘记)
- W_f·[h_{t-1}, x_t] + b_f:这才是真正的"决策委员会":
x_t(当前输入):相当于你现在看到的新信息(如看到老照片)h_{t-1}(上一隐藏状态):相当于你当前的记忆状态(如最近常回忆过去)- 权重
W_f和偏置b_f:相当于你的性格倾向(天生健忘还是念旧)
σ只是执行者,而[h_{t-1}, x_t]才是真正的决策依据!
- 结构分析:
- 输入:前一时刻隐含状态ht−1 + 当前输入xt(拼接)
- 通过全连接层 + sigmoid激活
- 输出门值ft(范围[0,1])
- 功能:
- 决定遗忘多少上一细胞状态Ct−1的信息
- 门值大小反映信息保留程度
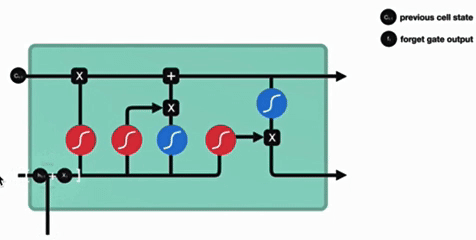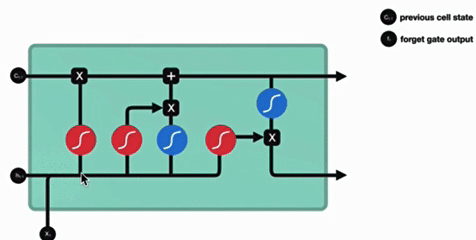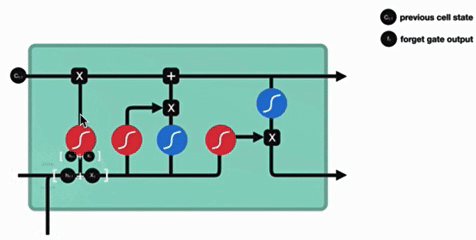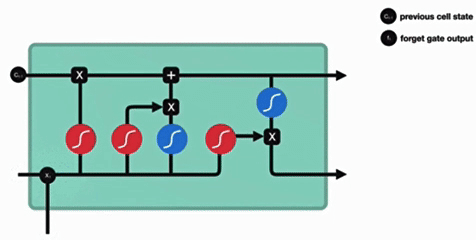
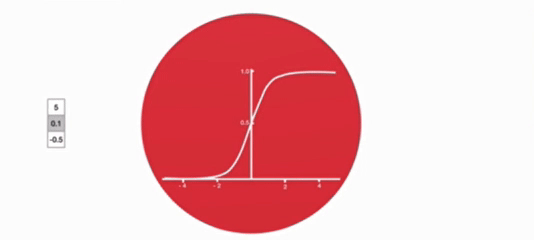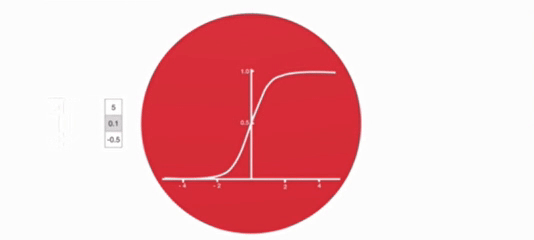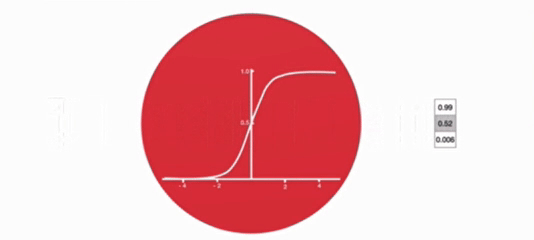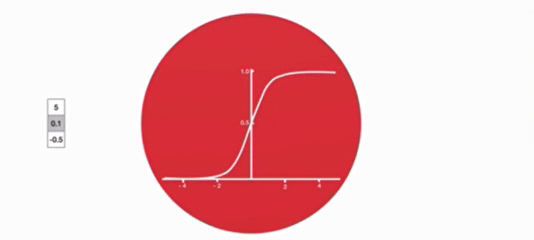
- 激活函数 sigmoid 作用:将值压缩在 0~1 之间,调节信息通过量
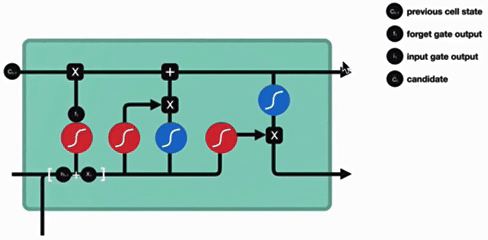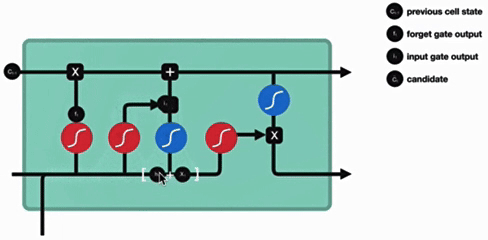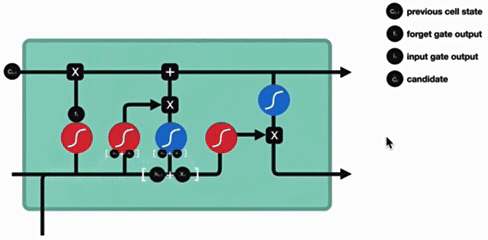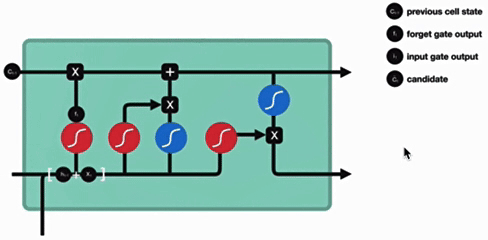
2. 输入门
输入门结构分析:
我们看到输入门的计算公式有两个,第一个就是产生输入门门值的公式,它和遗忘门公式几乎相同,区别只是在于它们之后要作用的目标上。这个公式意味着输入信息有多少需要进行过滤。输入门的第二个公式是与传统RNN的内部结构计算相同。对于LSTM来讲,它得到的是当前的细胞状态,而不是像经典RNN一样得到的是隐含状态。
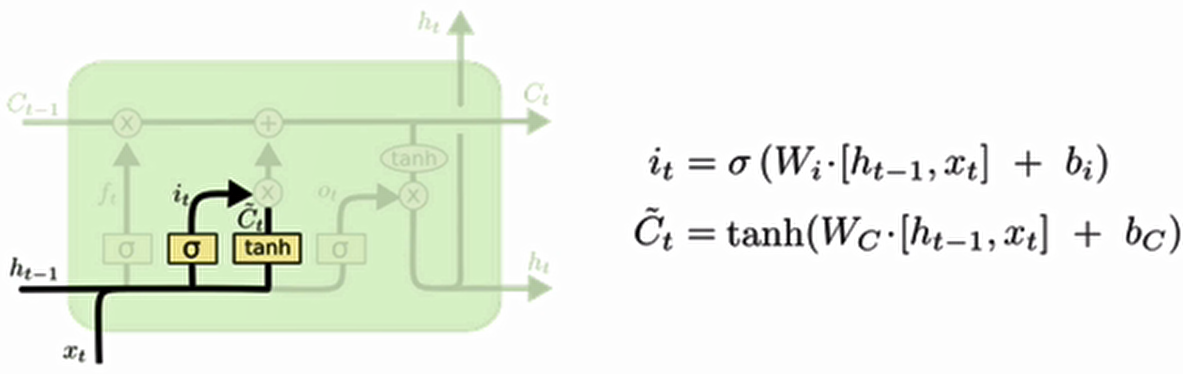
- 计算公式:
- 门值:
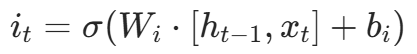
- 候选细胞状态:

- 门值:
- 结构分析:
- 门值计算与遗忘门结构相同(不同参数)
- 候选状态计算类似传统RNN(使用tanh激活)
- 功能:
- 筛选当前输入中有价值的信息
- 与遗忘门协同更新细胞状态
3. 细胞状态更新
细胞状态更新分析:
细胞更新的结构与计算公式非常容易理解,这里没有全连接层,只是将刚刚得到的遗忘门门值与上一个时间步得到的C(t-1)相乘,再加上输入门门值与当前时间步得到的未更新C(t)相乘的结果.最终得到更新后的C(t)作为下一个时间步输入的一部分.整个细胞状态更新过程就是对遗忘门和输入门的应用.
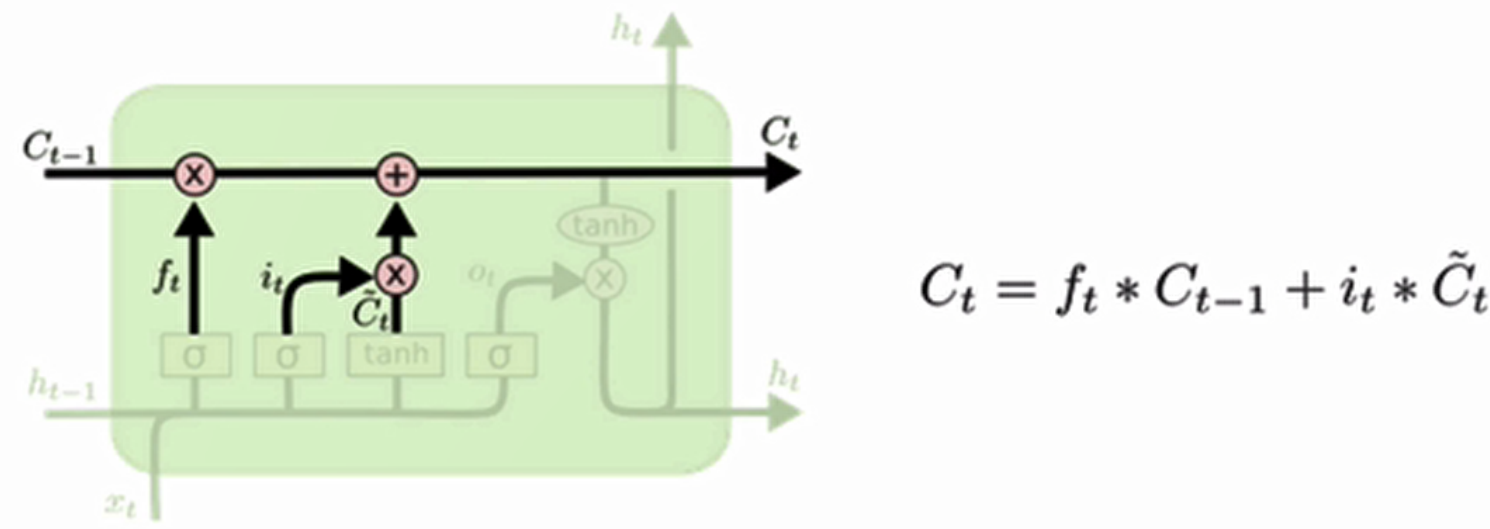
- 更新逻辑:
- 遗忘部分旧状态(ft⊙Ct−1)
- 添加部分新信息
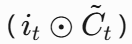
- 特点:
- 线性操作(无激活函数)
- 实现长期记忆的保留与更新
- 更新分析:
- 无全连接层,直接通过遗忘门和输入门作用于历史状态和新信息
- 本质是 "遗忘部分历史信息 + 保留部分新信息" 的过程,更新后的Ct作为下一时间步输入
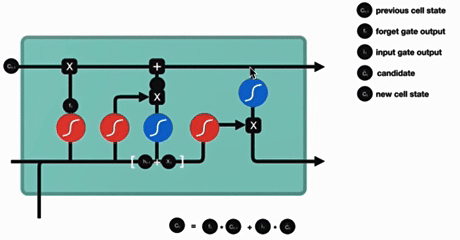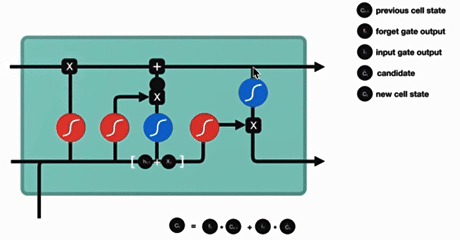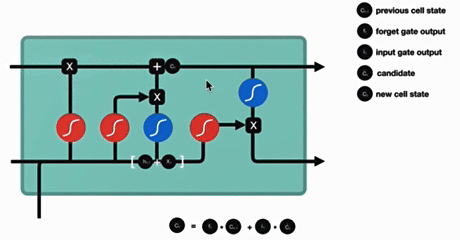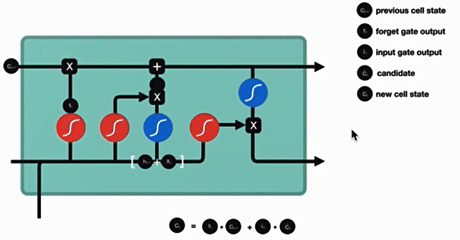
4. 输出门
输出门结构分析:
输出门部分的公式也是两个,第一个即是计算输出门的门值,它和遗忘门,输入门计算方式相同。第二个即是使用这个门值产生隐含状态h(t),他将作用在更新后的细胞状态C(t)上,并做tanh激活,最终得到h(t)作为下一时间步输入的一部分,整个输出门的过程,就是为了产生隐含状态h(t)。
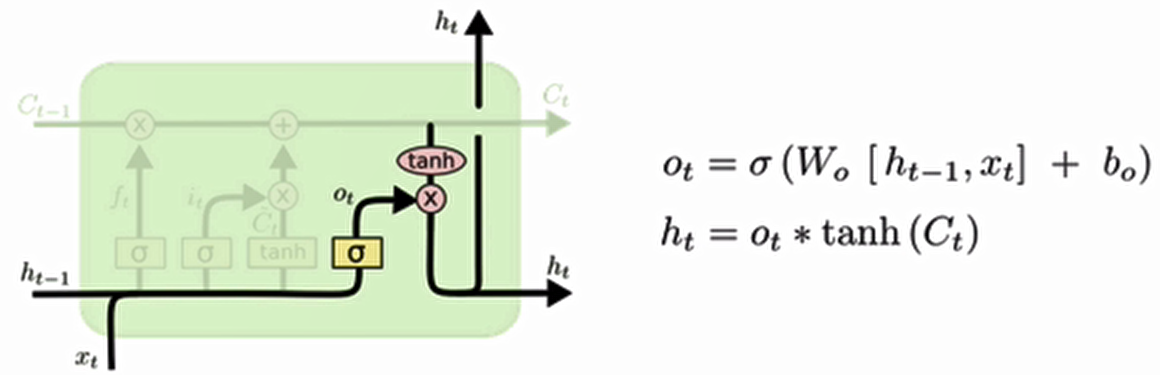
- 计算公式:
- 门值:
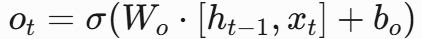
- 隐状态:

- 门值:
- 结构分析:
- 门值ot(范围 0~1)控制细胞状态的输出比例
- 隐状态ht由门值与tanh(Ct)(范围 - 1~1)相乘得到,作为下一时间步输入
- 核心作用是生成当前时间步的隐状态ht
- 功能:
- 控制当前细胞状态的暴露程度
- 生成最终隐含状态供下一时间步使用
Bi-LSTM(双向 LSTM)
- 原理:
- 不改变 LSTM 内部结构
- 同时运行正向和反向LSTM
- 拼接两次计算的结果作为最终输出
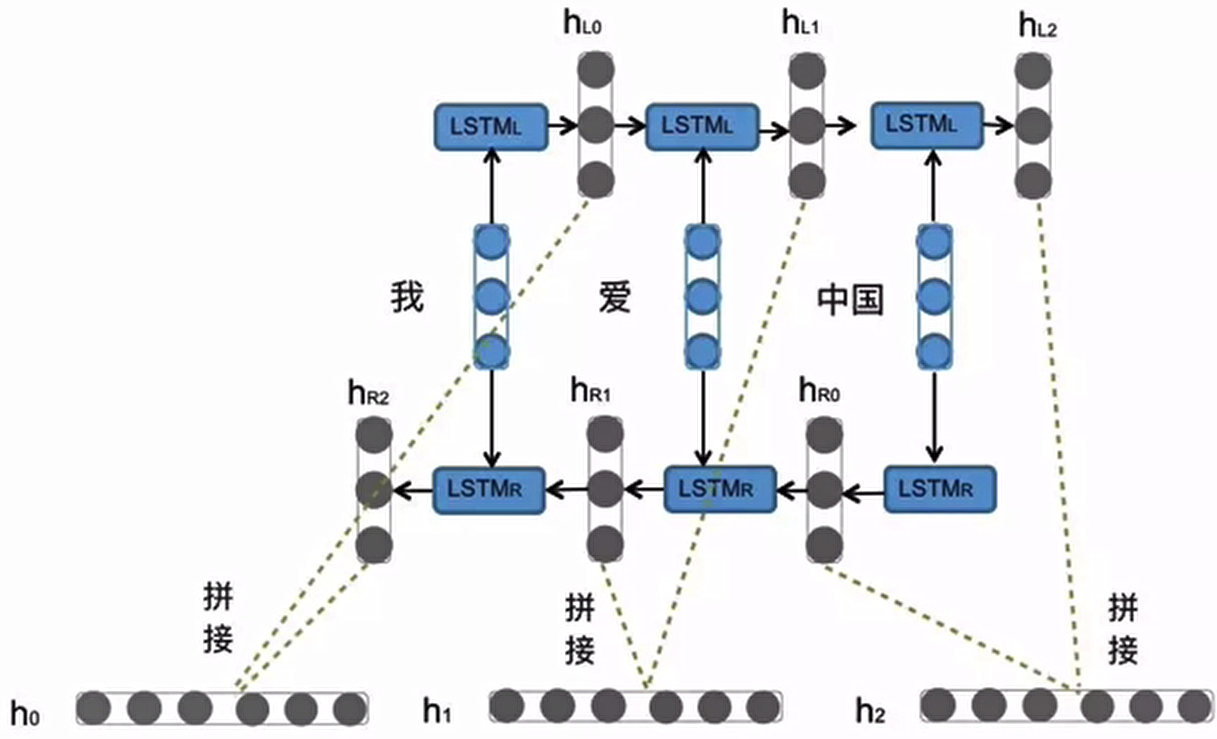
Bi-LSTM结构分析:
我们看到图中对“我爱中国”这句话或者叫这个输入序列,进行了从左到右和从右到左两次LSTM处理,将得到的结果张量进行了拼接作为最终输出。这种结构能够捕捉语言语法中一些特定的前置或后置特征,增强语义关联,但是模型参数和计算复杂度也随之增加了一倍,一般需要对语料和计算资源进行评估后决定是否使用该结构。
- 优势:
- 捕捉前后文语境特征
- 增强语义关联理解
- 代价:
- 参数量和计算量翻倍
- 需根据语料和算力评估计算资源是否充足
Pytorch 中 LSTM 的使用
LSTM初始化参数(创建模型时配置)
lstm = nn.LSTM( input_size=5, hidden_size=6, num_layers=2, bidirectional=False )| 参数名 | 作用说明 | 示例值 | 注意事项 |
|---|---|---|---|
input_size |
输入数据的特征维度(如词向量维度) | 5 | 必须与输入数据最后一维一致 |
hidden_size |
隐藏状态的维度(记忆容量) | 6 | 决定模型记忆能力大小 |
num_layers |
堆叠的LSTM层数 | 2 | 层数越多模型越复杂 |
bidirectional |
是否为双向LSTM | False | 双向时会加倍输出维度 |
前向传播参数(调用模型时输入)
output, (hn, cn) = lstm(input, (h0, c0))输入参数:
| 参数 | 形状说明 | 示例形状 | 作用 |
|---|---|---|---|
input |
(seq_len, batch_size, input_size) |
(10, 3, 5) | 输入序列(10步,batch=3) |
h0 |
(num_layers*方向数, batch, hidden_size) |
(2, 3, 6) | 初始隐藏状态(如全零初始化) |
c0 |
同h0形状 |
(2, 3, 6) | 初始细胞状态 |
输出参数:
| 输出项 | 形状说明 | 示例输出形状 | 含意 |
|---|---|---|---|
output |
(seq_len, batch, hidden_size*方向数) |
(10, 3, 6) | 所有时间步的隐藏状态 |
hn |
同h0形状 |
(2, 3, 6) | 最后一个时间步的隐藏状态 |
cn |
同c0形状 |
(2, 3, 6) | 最后一个时间步的细胞状态 |
关键概念图解
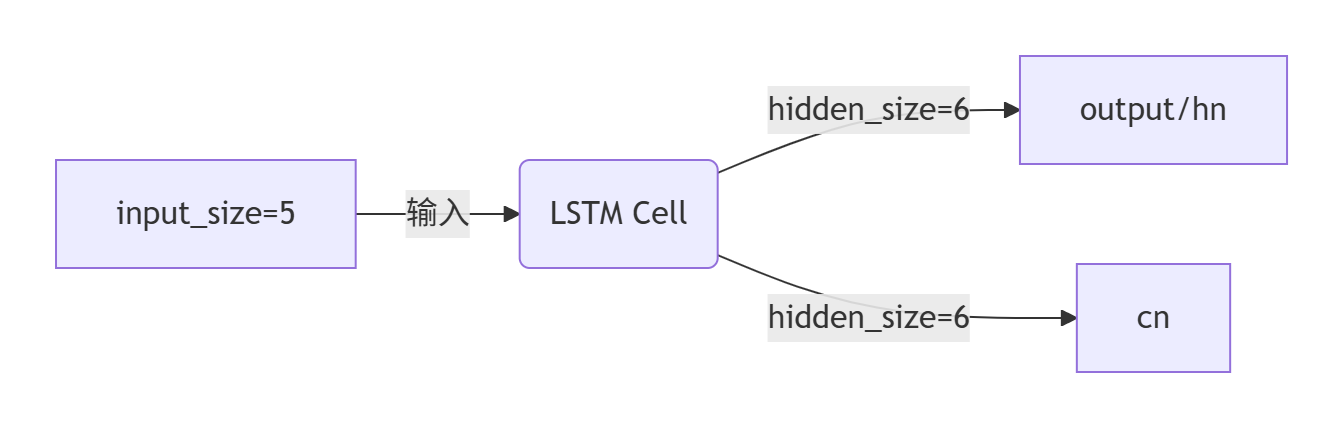
代码示例
import torch.nn as nn
import torch
# 定义LSTM:input_size=5,hidden_size=6,num_layers=2
rnn = nn.LSTM(5, 6, 2)
# 输入张量:sequence_length=1,batch_size=3,input_size=5
input = torch.randn(1, 3, 5)
# 初始化隐状态和细胞状态:num_layers×num_directions=2,batch_size=3,hidden_size=6
h0 = torch.randn(2, 3, 6)
c0 = torch.randn(2, 3, 6)
# 前向传播
output, (hn, cn) = rnn(input, (h0, c0))
# 输出结果
print("output:", output)
print("最后隐状态hn:", hn)
print("最后细胞状态cn:", cn)查看打印结果
output:
tensor([[[-0.5387, 0.3468, 0.4146, 0.2536, -0.2615, 0.0667],
[-0.0072, -0.1814, 0.0936, 0.1356, -0.4559, 0.1720],
[-0.2224, 0.2977, 0.4252, -0.2934, 0.0819, 0.1203]]],
grad_fn=<MkldnnRnnLayerBackward0>)
最后隐状态hn:
tensor([[[-0.1427, -0.2920, -0.1963, -0.1874, -0.0126, -0.5496],
[ 0.0570, 0.1978, -0.1338, 0.1485, 0.1445, -0.4599],
[ 0.3210, -0.0794, -0.1845, 0.0285, 0.3966, 0.1899]],
[[-0.5387, 0.3468, 0.4146, 0.2536, -0.2615, 0.0667],
[-0.0072, -0.1814, 0.0936, 0.1356, -0.4559, 0.1720],
[-0.2224, 0.2977, 0.4252, -0.2934, 0.0819, 0.1203]]],
grad_fn=<StackBackward0>)
最后细胞状态cn:
tensor([[[-0.2624, -0.5144, -0.5639, -0.5489, -0.0518, -0.8765],
[ 0.6077, 0.2968, -0.5591, 0.2557, 0.2518, -0.9615],
[ 1.1608, -0.5608, -0.4439, 0.0528, 0.6316, 0.4187]],
[[-0.8019, 0.8717, 0.7672, 0.5314, -0.5260, 0.0815],
[-0.0245, -0.7748, 0.3983, 0.3183, -0.9727, 0.3557],
[-0.4340, 0.4418, 0.7524, -0.8154, 0.2270, 0.1626]]],
grad_fn=<StackBackward0>)关键细节补充
- 激活函数选择:
- 门控使用sigmoid(输出[0,1])
- 状态计算使用tanh(输出[-1,1])
- 细胞状态特点:
- 贯穿整个时间序列
- 通过线性变换实现信息传递
- 现代变体:
- Peephole LSTM(增加细胞状态到门控的连接)
- GRU(简化版LSTM,合并门控)
LSTM 的优缺点
- 优势:通过门结构有效减缓长序列中的梯度消失 / 爆炸,在长序列任务上表现优于传统 RNN
- 缺点:内部结构复杂,同等算力下训练效率低于传统 RNN
GRU 模型
学习目标:
- 了解 GRU 内部结构及计算公式.
- 掌握 Pytorch 中 GRU 工具的使用.
- 了解 GRU 的优势与缺点.
- 更新门
- 重置门
GRU 的内部结构图和计算公式:


GRU 的更新门和重置门结构图:
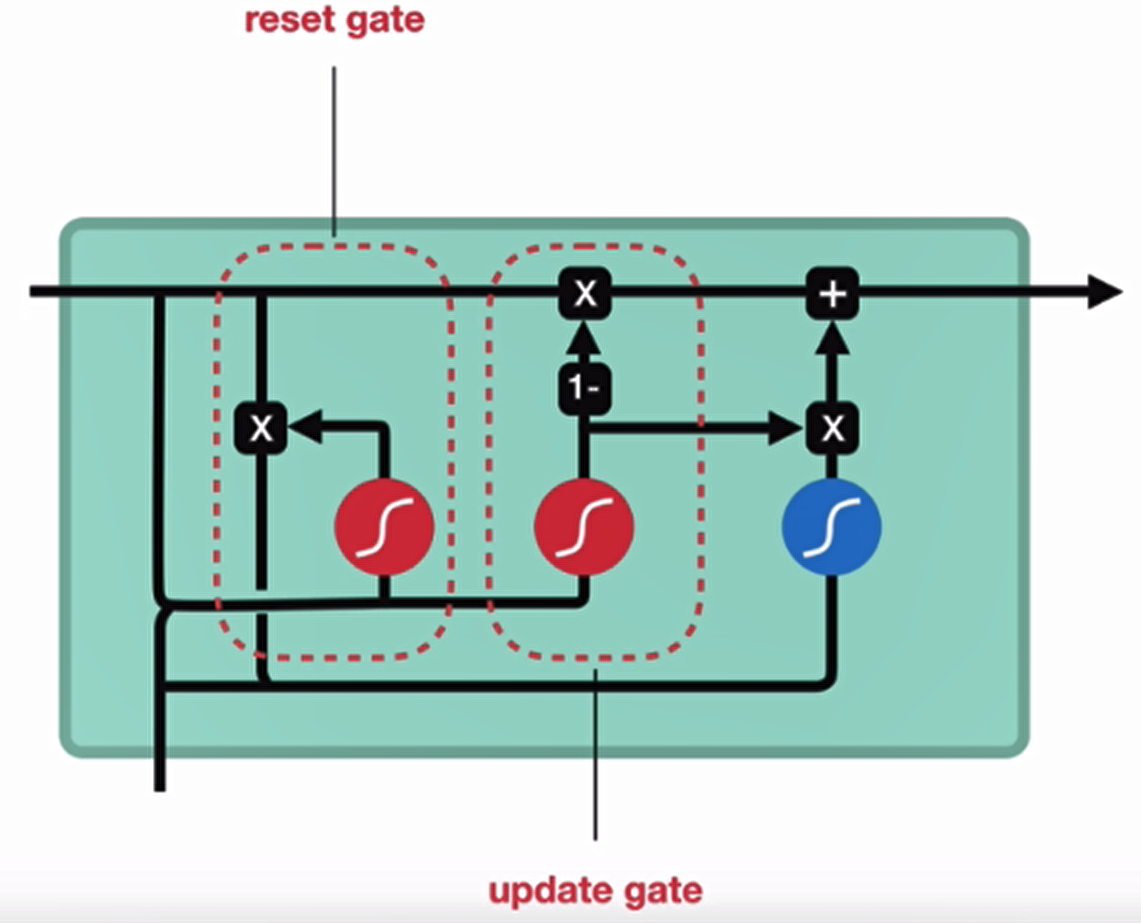
内部结构分析:
Pytorch 中 GRU 工具的使用
-
GRU初始化参数(创建模型时配置)
gru = nn.GRU( input_size=5, hidden_size=6, num_layers=2, bidirectional=False )参数名 作用说明 示例值 与LSTM的区别 input_size输入数据的特征维度(如词向量维度) 5 同LSTM hidden_size隐藏状态的维度(记忆容量) 6 同LSTM num_layers堆叠的GRU层数 2 同LSTM bidirectional是否为双向GRU False 同LSTM
前向传播参数(调用模型时输入)
output, hn = gru(input, h0) # GRU没有细胞状态(cell state)输入参数:
参数 形状说明 示例形状 与LSTM的区别 input(seq_len, batch_size, input_size)(10, 3, 5) 同LSTM h0(num_layers*方向数, batch, hidden_size)(2, 3, 6) 不需要 c0(GRU无细胞状态)输出参数:
输出项 形状说明 示例输出形状 与LSTM的区别 output(seq_len, batch, hidden_size*方向数)(10, 3, 6) 同LSTM hn同 h0形状(2, 3, 6) 只有隐藏状态,无 cn输出
关键对比:GRU vs LSTM
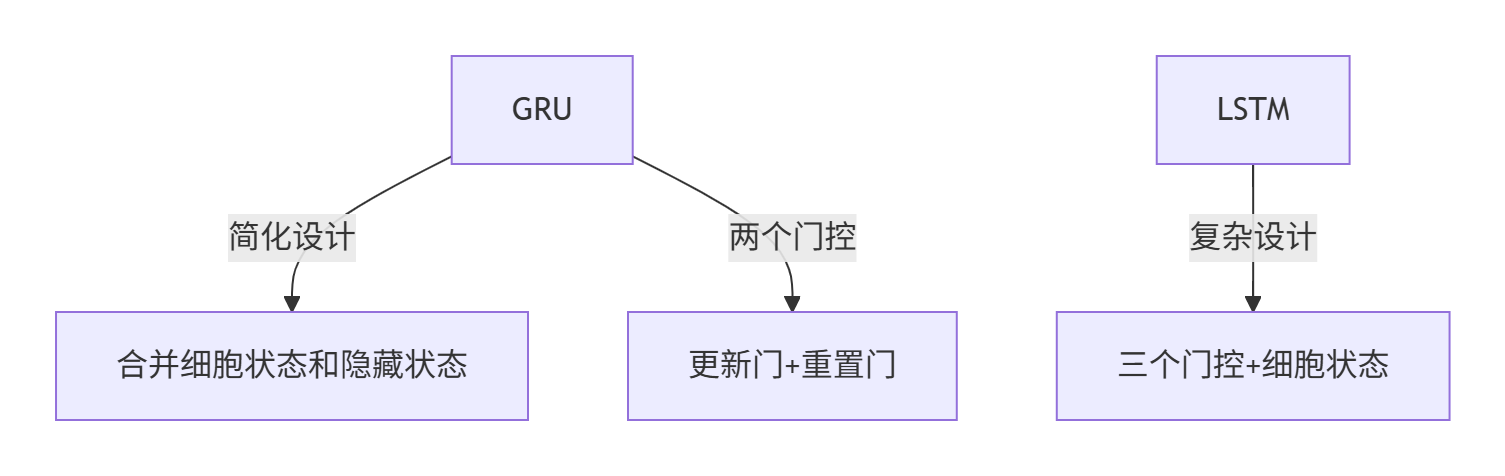
- 参数更少:GRU比LSTM少一个门控(LSTM有输入/遗忘/输出门,GRU只有更新/重置门)
- 计算更快:GRU的参数量减少约25%,适合对速度敏感的场景
- 输出差异:GRU不返回细胞状态(
cn),隐藏状态hn已包含全部记忆信息
典型代码示例
import torch
import torch.nn as nn
# 初始化GRU(双向双层)
gru = nn.GRU(input_size=5, hidden_size=6, num_layers=2, bidirectional=True)
# 输入数据(序列长度=10, batch=3)
input = torch.randn(10, 3, 5)
h0 = torch.zeros(4, 3, 6) # 形状:(2层×2方向, batch, hidden_size)
# 前向传播
output, hn = gru(input, h0)
print(output.shape) # torch.Size([10, 3, 12]) # 双向时hidden_size×2
print(hn.shape) # torch.Size([4, 3, 6]) # 每层每方向的最终状态
import torch
import torch.nn as nn
rnn = nn.GRU(5, 6, 2)
input = torch.randn(1, 3, 5)
h0 = torch.randn(2, 3, 6)
output, hn = rnn(input, h0)
print(output)
# tensor([[[-0.2097, -2.2225, 0.6204, -0.1745, -0.1749, -0.0460],
# [-0.3820, 0.0465, -0.4798, 0.6837, -0.7894, 0.5173],
# [-0.0184, -0.2758, 1.2482, 0.5514, -0.9165, -0.6667]]],
# grad_fn=<StackBackward>)
print(hn)
# tensor([[[ 0.6578, -0.4226, -0.2129, -0.3785, 0.5070, 0.4338],
# [-0.5072, 0.5948, 0.8083, 0.4618, 0.1629, -0.1591],
# [ 0.2430, -0.4981, 0.3846, -0.4252, 0.7191, 0.5420]],
# [[-0.2097, -2.2225, 0.6204, -0.1745, -0.1749, -0.0460],
# [-0.3820, 0.0465, -0.4798, 0.6837, -0.7894, 0.5173],
# [-0.0184, -0.2758, 1.2482, 0.5514, -0.9165, -0.6667]]],
# grad_fn=<StackBackward>)GRU 的优缺点
GRU 的优势:
- GRU和LSTM作用相同,在捕捉长序列语义关联时,能有效抑制梯度消失或爆炸,效果都优于传统RNN
- 计算复杂度相比LSTM要小
GRU 的缺点:
- GRU仍然不能完全解决梯度消失问题
- 作为RNN的变体,有着RNN结构本身的一大弊端,即不可并行计算,这在数据量和模型体量逐步增大的未来,是RNN发展的关键瓶颈




 浙公网安备 33010602011771号
浙公网安备 33010602011771号