12.卷积神经网络CNN
全连接神经网络处理图像存在的问题
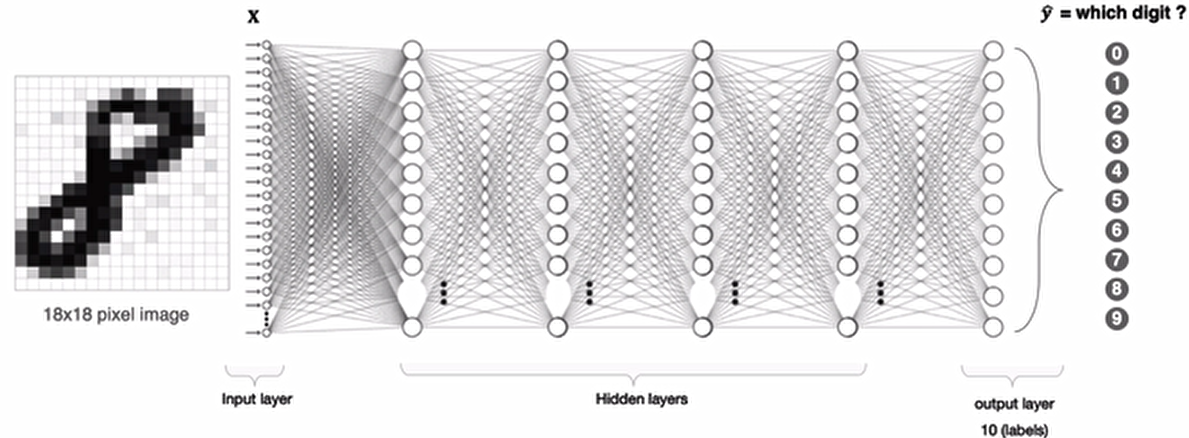
利用全连接神经网络对图像进行处理存在以下两个问题
- 需要处理的数据量大,效率低假如我们处理一张 1000x1000 像素的图片,参数量如下:
1000x1000x3=3,000,000
这么大量的数据处理起来是非常消耗资源的
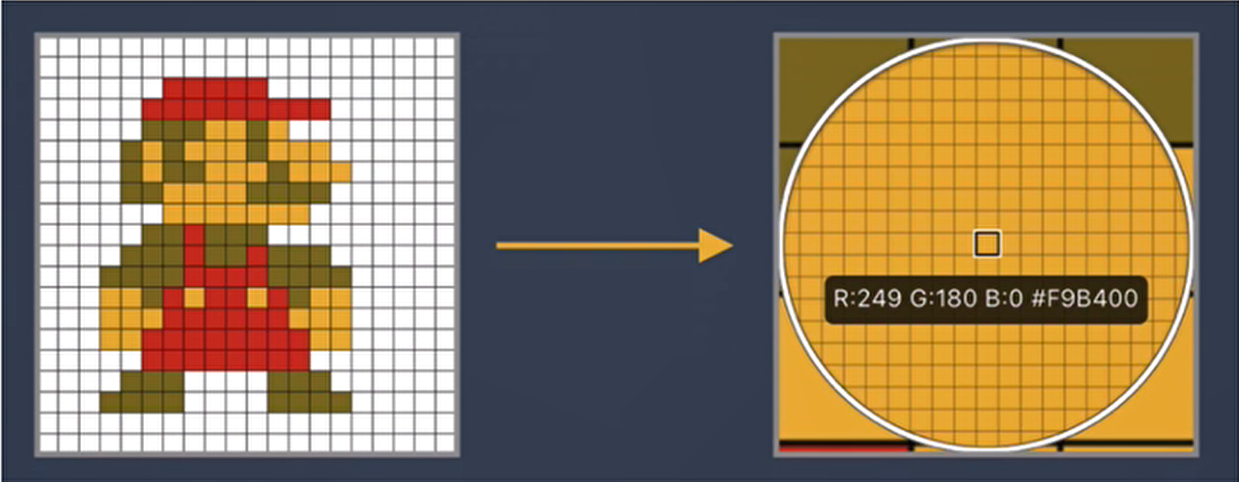
- 图像在维度调整的过程中很难保留原有的特征,导致图像处理的准确率不高

假如有圆形是1,没有圆形是0,那么圆形的位置不同就会产生完全不同的数据表达。但是从图像的角度来看,图像的内容(本质)并没有发生变化,只是位置发生了变化。所以当我们移动图像中的物体,用全连接升降得到的结果会差异很大,这是不符合图像处理的要求的。
CNN网络的构成
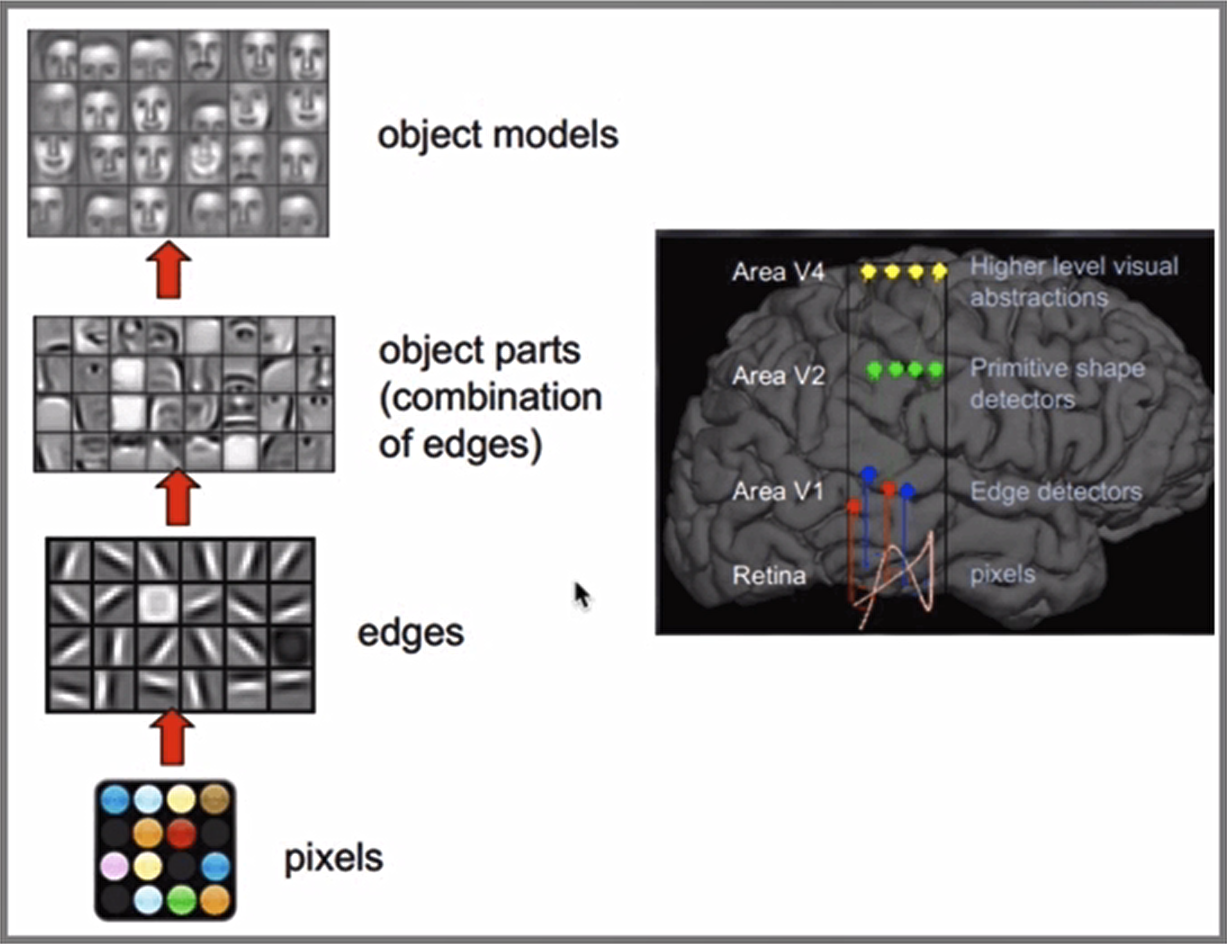
CNN(Convolutional Neural Network)网络受人类视觉神经系统的启发,人类的视觉原理:从原始信号摄入开始(瞳孔摄入像素Pixels),接着做初步处理(大脑皮层某些细胞发现边缘和方向),然后抽象(大脑判定,眼前的物体的形状,是圆形的),然后进一步抽象(大脑进一步判定该物体是只人脸)。下面是人脑进行人脸识别的一个示例:
CNN网络主要有三部分构成:卷积层、池化层和全连接层构成:
- 卷积层负责提取图像中的局部特征;
- 池化层用来大幅降低参数量级(降维);
- 全连接层类似人工神经网络的部分,用来输出想要的结果。

整个CNN网络结构如下图所示:

卷积层
卷积层是卷积神经网络中的核心模块,卷积层的目的是提取输入特征图的特征,如下图所示,卷积核可以提取图像中的边缘信息

卷积的计算方法
那卷积是怎么进行计算的呢?
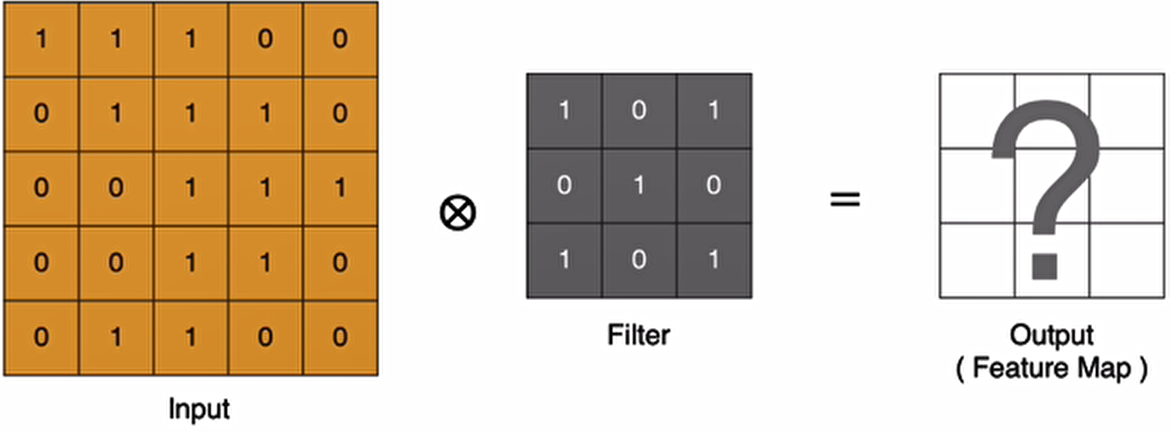
(上面是使用的是3x3的卷积核(Fliter))
关于卷积核详解,参照文末:卷积核
卷积运算本质上就是在滤波器和输入数据的局部区域间做点积。
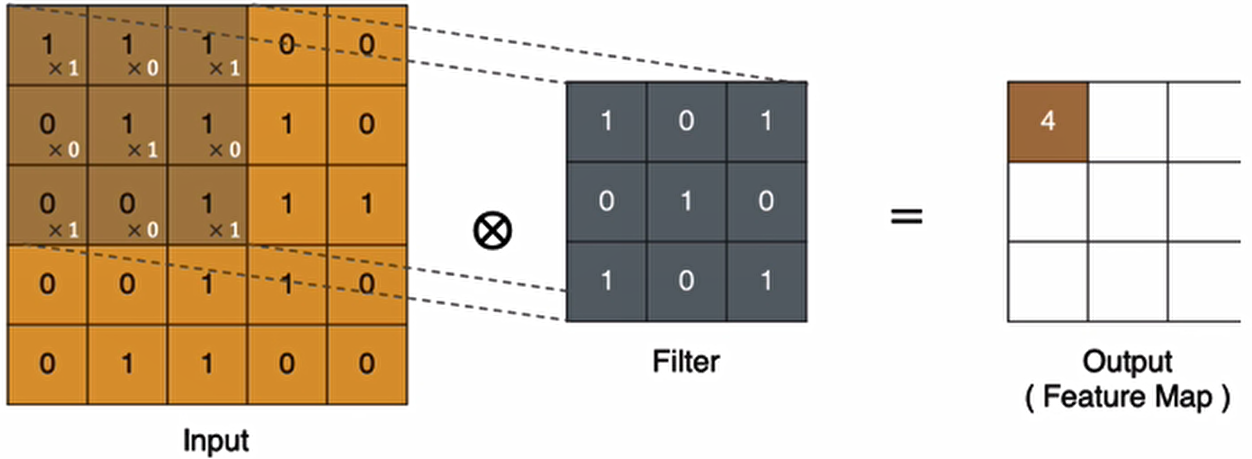
左上角的点计算方法:
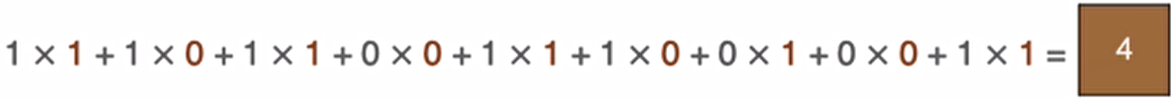
同理可以计算其他各点,得到最终的卷积结果
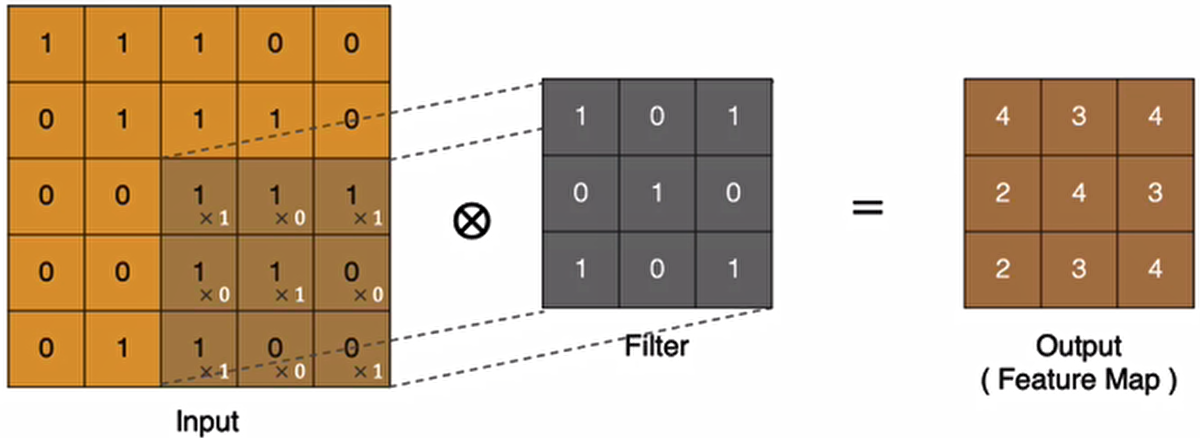
最后一个点的计算过程为:

padding
在上述卷积过程中,特征图比原始图减小了很多,我们可以在原图像的周围进行padding,来保证在卷积过程中特征图大小不变(其实就是在周围添加一层或者多层“0”)
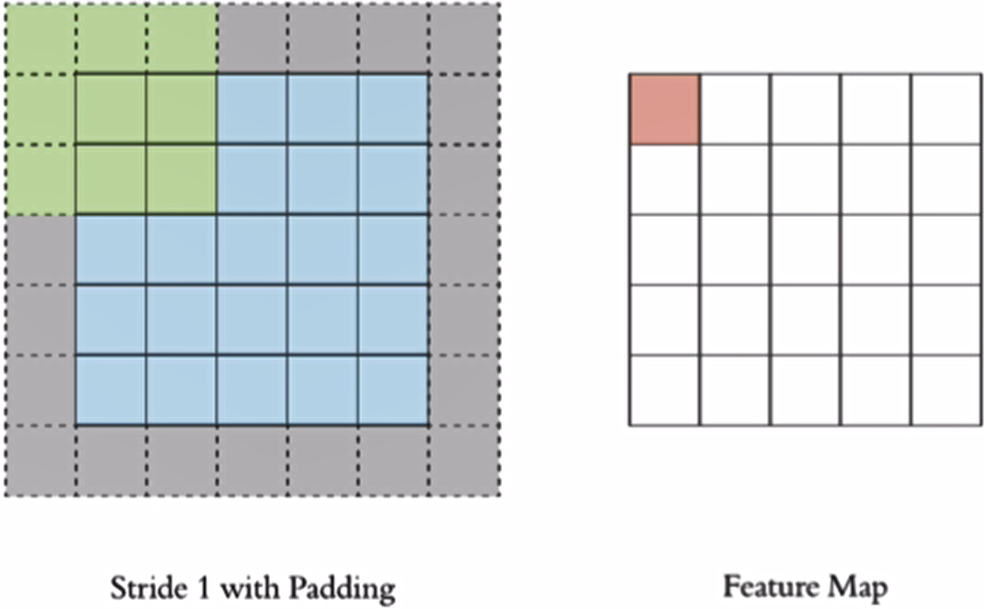
stride
按照步长为1来移动卷积核,计算特征图如下所示

如果我们把stride增大,比如设为2,也是可以提取特征图的,如下图所示:
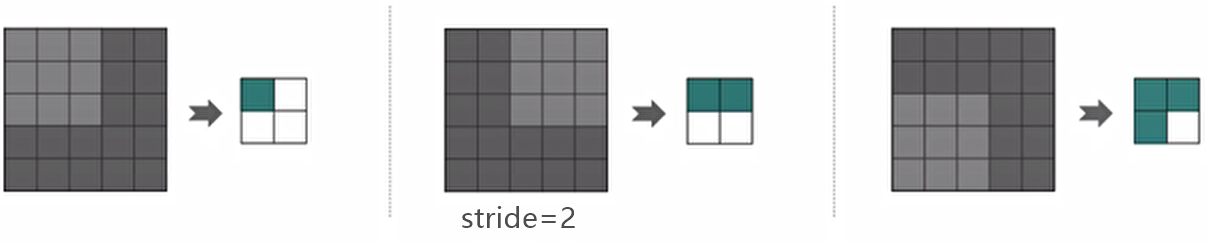
步长增大也能起到降维的作用
多通道卷积
实际中的图像都是多个通道组成的,我们怎么计算卷积呢?
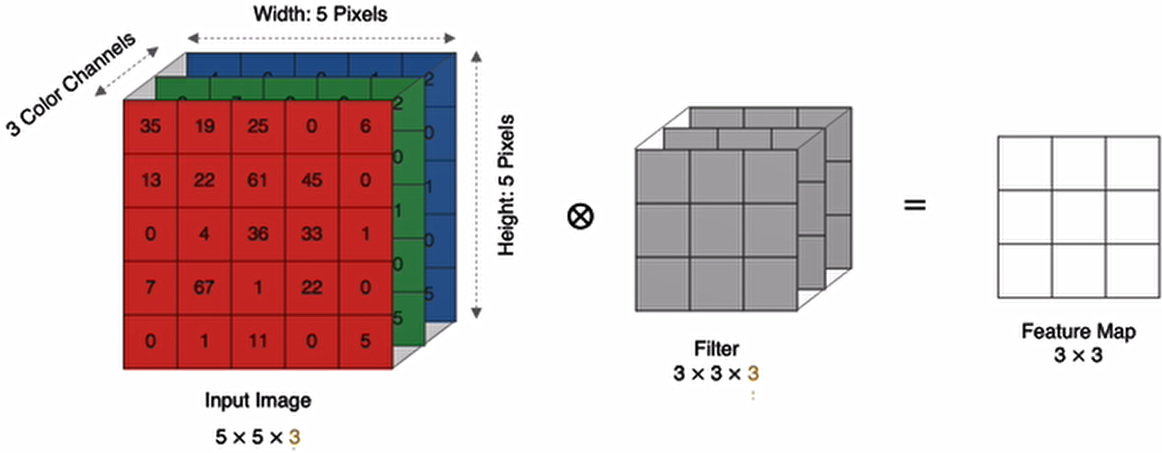
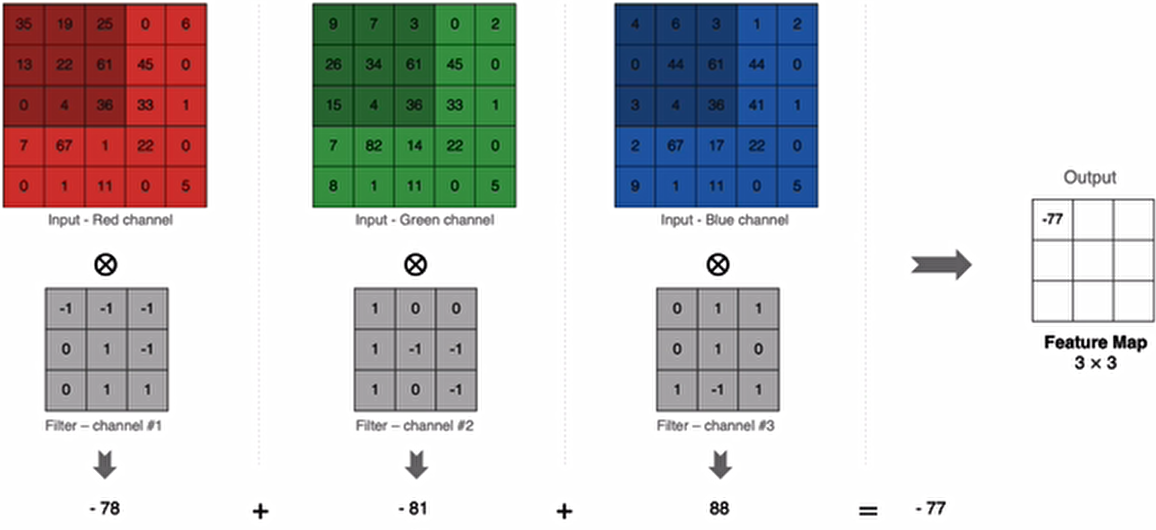
计算方法如下:当输入有多个通道(channel)时(例如图片可以有 RGB 三个通道),卷积核需要拥有相同的channel数,每个卷积核 channel 与输入层的对应 channel 进行卷积,将每个 channel的卷积结果按位相加得到最终的 Feature Map
多卷积核卷积
如果有多个卷积核时怎么计算呢?当有多个卷积核时,每个卷积核学习到不同的特征,对应产生包含多个 channel 的 Feature Map,例如下图有两个 filter,所以 output 有两个 channel。

特征图大小
输出特征图的大小与以下参数息息相关:
- *size:卷积核/过滤器大小,一般会选择为奇数,比如有:1*1,3*3,5*5
- *padding:零填充的方式
- *stride:步长
计算方法如下所示:
- 输入体积大小H1*W1*D1(H:高,W:宽,D:通道数)
- 四个超参数:
- Filter数量K(卷积核个数)
- Filter大小F(卷积核大小)
- 步长S
- 零填充大小P
- 输出体积大小H2*W2*D2
- H2=(H1-F+2P)/S+1
- W2=(W1-F+2P)/S+1
- D2=K
输入特征图为5x5,卷积核为3x3,外加padding为1,则其输出尺寸为:
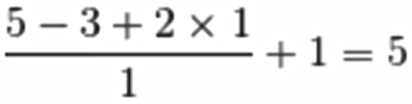
如下图所示:
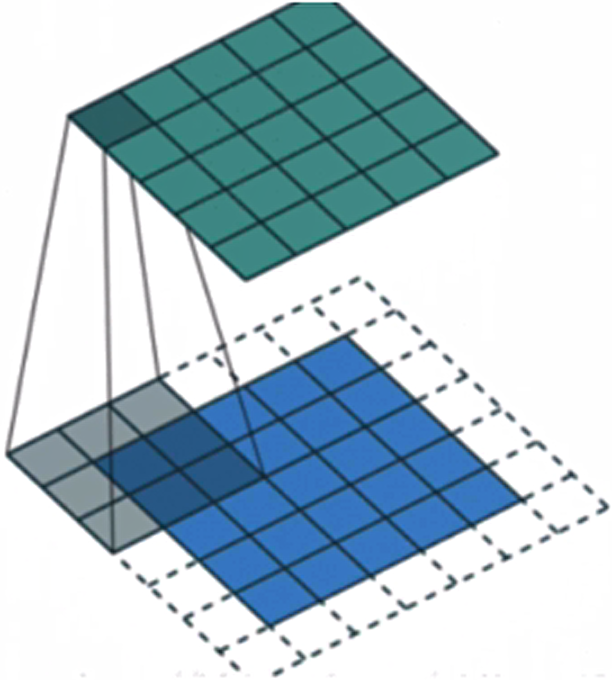
在tf.keras中卷积核的实现使用:
tf.keras.layers.Conv2D(filters,kernel_size,strides=(1,1),padding='valid',activation=None)主要参数说明:
| 参数 | 描述 |
|---|---|
| filters | 卷积过滤器的数量,对应输出特征图的通道数 |
| kernel_size | 过滤器 filter 的大小 |
| strides | 步长 |
| padding |
valid: 在输入周围不进行 padding;(padding=0) same: padding 后使输出特征图和输入特征图形状相同 |
| activation | 激活函数 |
池化层(Pooling)
池化层用来降低后续网络层的输入维度,缩减模型大小,提高计算速度,并提高了Feature Map的鲁棒性,防止过拟合。
它主要对卷积层学习到的特征图进行下采样(subsampling)处理,主要有两种:最大池化,平均池化
最大池化(推荐)
- Max Pooling,取窗口内的最大值作为输出,这种方式使用较广泛。

在tf.keras的实现使用:
tf.keras.layers.MaxPool2D(pool_size=(2,2),strides=None,padding='valid')参数:
- pool_size:池化窗口的大小
- strides:窗口移动的步长,默认为1
- padding:是否进行填充,默认是不进行填充的
平均池化
Avg Pooling,取窗口内的所有值的均值作为输出
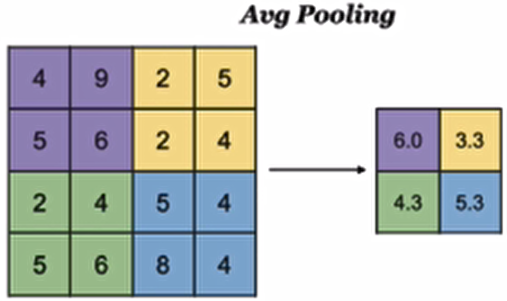
在tf.keras的实现使用:
tf.keras.layers.AveragePooling2D(pool_size=(2,2),strides=None,padding='valid')全连接层
全连接层位于CNN网络的末端,经过卷积层的特征提取与池化层的降维后,将特征图转换成一维向量送入到全连接层中进行分类或回归的操作。
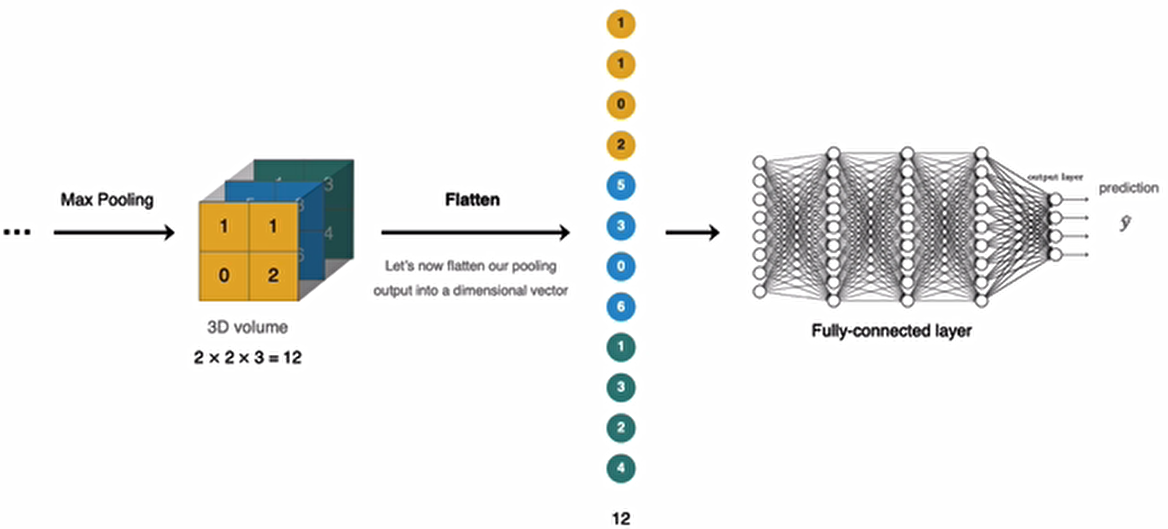
在tf.keras中全连接层使用tf.keras.dense实现。
LeNet-5卷积神经网络的构建
我们构建卷积神经网络在mnist数据集上进行处理,如下图所示:LeNet-5是一个较简单的卷积神经网络,输入的二维图像,先经过两次卷积层,池化层,再经过全连接层,最后使用softmax分类作为输出层。
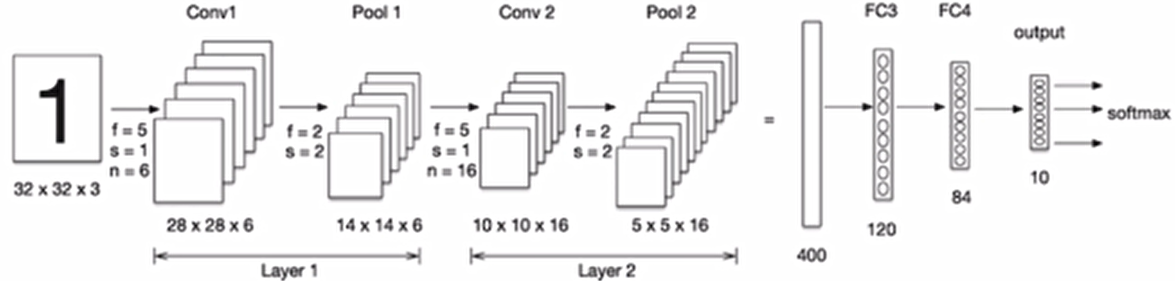
导入工具包:
import tensorflow as tf
from tensorflow.keras.datasets import mnist数据集加载
(x_train,y_train),(x_test,y_test)=mnist.load_data()
x_train.shape,y_train.shape,x_test.shape,y_test.shape#((60000, 28, 28), (60000,), (10000, 28, 28), (10000,))数据处理
卷积神经网络的输入要求是:NHWC,分别是图片数量,图片高度,图片宽度和图片的通道,因为是灰度图,通道为1.
# 数据处理num,H,W,C
# 训练集
train_imags=tf.reshape(x_train,(x_train.shape[0],x_train.shape[1],x_train.shape[2],1))
# 测试集
test_imags=tf.reshape(x_test,(x_test.shape[0],x_test.shape[1],x_test.shape[2],1))
train_imags.shape,test_imags.shape#(TensorShape([60000, 28, 28, 1]), TensorShape([10000, 28, 28, 1]))模型搭建
Lenet-5模型输入的二维图像,先经过两次卷积层,池化层,再经过全连接层,最后使用softmax分类作为输出层,模型构建如下:
net=tf.keras.models.Sequential([
tf.keras.layers.Input(shape=(28,28,1)),
#卷积层:6个5*5的卷积核,激活函数是sigmoid
tf.keras.layers.Conv2D(filters=6,kernel_size=5,activation='sigmoid'),
# 最大池化
tf.keras.layers.MaxPool2D(pool_size=2,strides=2),
#卷积层:16个5*5的卷积核,激活函数是sigmoid
tf.keras.layers.Conv2D(filters=16,kernel_size=5,activation='sigmoid'),
# 最大池化
tf.keras.layers.MaxPool2D(pool_size=2,strides=2),
# 维度调整为1维数据
tf.keras.layers.Flatten(),
# 全连接层,激活‘sigmoid’
tf.keras.layers.Dense(120,activation='sigmoid'),
# 全连接层,激活‘sigmoid’
tf.keras.layers.Dense(80,activation='sigmoid'),
# 全连接层,激活‘sigmoid’
tf.keras.layers.Dense(10,activation='softmax')
])
net.summary()Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ conv2d (Conv2D) │ (None, 24, 24, 6) │ 156 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d (MaxPooling2D) │ (None, 12, 12, 6) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_1 (Conv2D) │ (None, 8, 8, 16) │ 2,416 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_1 (MaxPooling2D) │ (None, 4, 4, 16) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten (Flatten) │ (None, 256) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense (Dense) │ (None, 120) │ 30,840 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_1 (Dense) │ (None, 80) │ 9,680 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_2 (Dense) │ (None, 10) │ 810 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 43,902 (171.49 KB)
Trainable params: 43,902 (171.49 KB)
Non-trainable params: 0 (0.00 B)模型编译
设置优化器和损失函数:
# 优化器
optimizer=tf.keras.optimizers.SGD(learning_rate=0.9)
# 模型编译:指定损失函数、优化器和评价指标
net.compile(optimizer=optimizer,loss='sparse_categorical_crossentropy',metrics=['accuracy'])#由于目标数据未进行热编码,所以选用sparse_categorical_crossentropy模型训练
net.fit(x_train,y_train,epochs=5,validation_split=0.1)Epoch 1/5
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 4s 2ms/step - accuracy: 0.2273 - loss: 2.0352 - val_accuracy: 0.9270 - val_loss: 0.2190
Epoch 2/5
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 4s 2ms/step - accuracy: 0.9463 - loss: 0.1711 - val_accuracy: 0.9742 - val_loss: 0.0889
Epoch 3/5
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 4s 2ms/step - accuracy: 0.9680 - loss: 0.1026 - val_accuracy: 0.9813 - val_loss: 0.0642
Epoch 4/5
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.9735 - loss: 0.0831 - val_accuracy: 0.9738 - val_loss: 0.0806
Epoch 5/5
1688/1688 ━━━━━━━━━━━━━━━━━━━━ 5s 3ms/step - accuracy: 0.9775 - loss: 0.0728 - val_accuracy: 0.9722 - val_loss: 0.0930<keras.src.callbacks.history.History at 0x1c006626450>模型评估
score=net.evaluate(x_test,y_test,verbose=1)
score313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - accuracy: 0.9652 - loss: 0.1076
[0.09157712757587433, 0.9710999727249146]与全连接相比,准确率提高了不少?
补充
卷积核
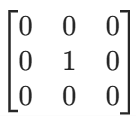
卷积核(也叫卷积滤波器、卷积矩阵 )是一个方阵,但对角线上不一定都是 1 ,它的数值完全由任务需求和设计目标决定,不同场景下卷积核的数值千差万别
| 常见误解 | 事实澄清 |
|---|---|
| 卷积核都是方阵 | 实际工程中非方核占比>30% |
| 卷积核是矩阵 | 卷积核是4维张量,不是矩阵 |
| 残差连接中的"恒等映射"说法 | 实际实现多用1×1卷积替代 |
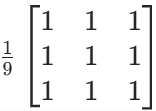
在基础的图像处理,如传统的数字图像处理领域,当进行简单的滤波操作(如边缘检测、图像平滑)时 ,卷积核一般是二维矩阵。比如常见的用于边缘检测的 Sobel 算子,是一个 3×3 的二维矩阵;用于图像平滑的均值滤波器,也是二维矩阵形式,像 3×3 的均值矩阵:
总结
其他疑问:
我们在使用卷积层的时候:
#卷积层:16个5*5的卷积核,激活函数是sigmoid
tf.keras.layers.Conv2D(filters=16,kernel_size=5,activation='sigmoid'), 核的个数和卷积核大小都是设置好的,为什么说他们的形状是随机生成的?这不矛盾吗?
另外,参数设置只有一个kernel_size来指定核的形状,那岂不是只能是方阵?
# 使用 3×5 的矩形卷积核(高=3,宽=5)
tf.keras.layers.Conv2D(filters=16, kernel_size=(3, 5), activation='sigmoid')问:也就是说,卷积核的形状我们初始化之后就不在变了,变的是里面的数值对吗?
在卷积神经网络(CNN)中,一旦定义好了卷积层,卷积核的形状就固定下来,在训练过程中保持不变,而变化的是卷积核里面的数值(权重参数) 。


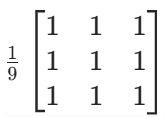
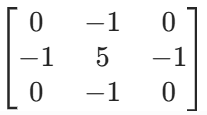



 浙公网安备 33010602011771号
浙公网安备 33010602011771号