09.批标准化（批量归一化）

这是一个三层神经网络：

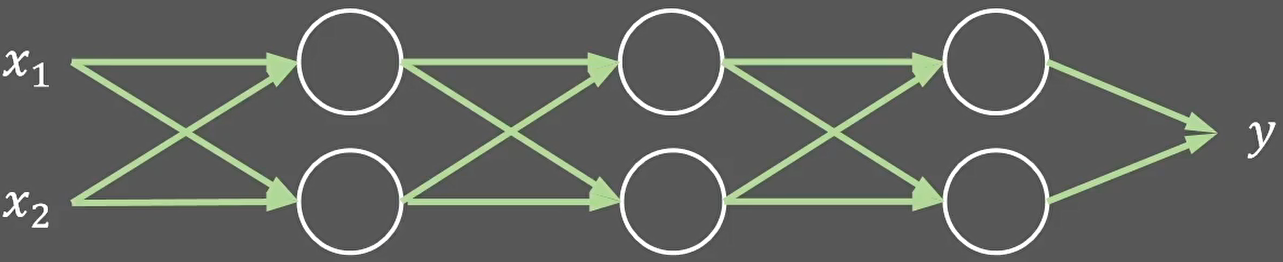
这是一个训练样本：

假设一共有30个训练样本X1~X30，并且我们使用小批量梯度下降的方式，每次选取五个样本进行训练，这五个样本我们称为一个批量（batch）。

假设某个batch样本服从下面的分布：

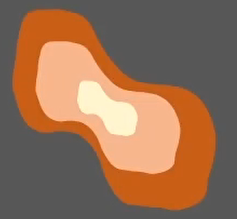
然后经过层次网络非线性变换之后，每层学习到的分布都将无法预测：

并且，前一层输出就是后一层网络输入，因此，由于参数的更新，每层的输入分布都在发生变化：

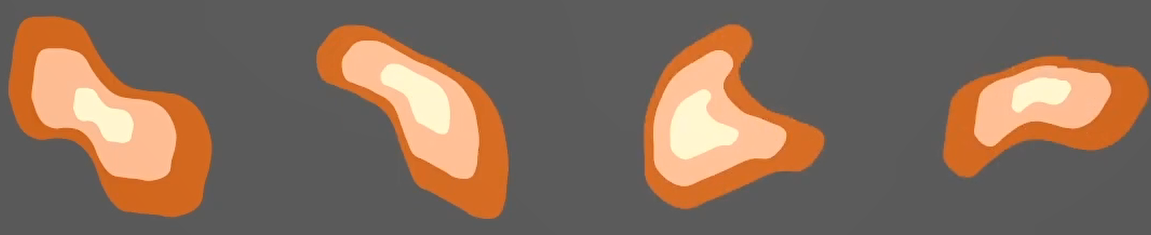
导致网络很难收敛；

为了让网络可以正常收敛，我们需要：学习率不能设置太大，参数初始化准确，网络层数不能过多。研究人员发现，这个现象是由于每层分布差异过大，并且无法预测导致的，那么如果让每一个batch内的样本在每一层中都服从相似的分布，不就可以解决上面的问题了吗：

这就是2015年提出的批标准化(BN层,Batch Normalization)：批量归一化方法。

批标准化(BN层,Batch Normalization)是2015年提出的一种方法，在进行深度网络训练时，大多会采取这种算法，与全连接层一样，BN层也是属于网络中的一层。

假设一个batch中存在X1到X5这五个样本，其中任意一个元素Xi通过第一层神经网络线性变换后得到输出Zi，那么由Z1到Z5构成的集合，就是下一层的输入，在进行下一层运算之前，我们首先计算Z1到Z5的平均值和标准差：

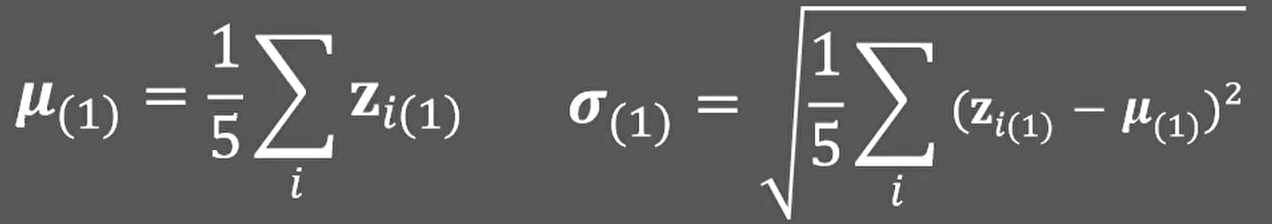
然后通过减去均值并除以标准差的方法将样本归一化到均值为0，标准差为1的分布中：

为了稳定数值计算，我们需要在分母添加一个极小值：ε，避免出现分母为0的情况：

并且，我们并不希望每层样本的分布都完全相同，因此，在通过一个线性计算进行简单的分布变化：

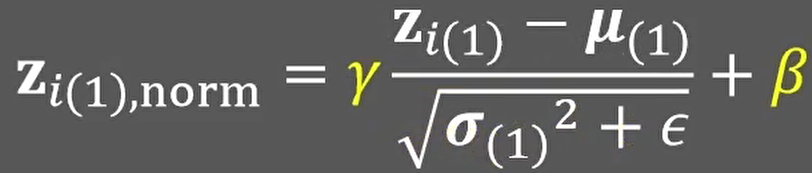
其中γ和β是可以学习的参数，随着训练过程自动调整。

以上就是Batch Normalization的运算过程。

如果我们在每层网络中都进行BN算法，也就能保证每一层的输入都是近似的。那么我们就可以使用：较大的学习率，尝试参数初始化方法（参数初始化不再敏感），并且加速训练过程。

 

注意，由于BN算法引入了需要学习的参数γ和β，因此在反向传播时更新的参数由2个变成了4个，但由于在归一化过程中，需要减掉所有向量的均值，因此偏置b向量可以不用参与计算，实际上需要更新的变量是3个。

另外，这里的神经元不只是进行了线性变换，他其实进行了三个运算：

理论上讲，后两个步骤的顺序并不是固定的，也可以先进行非线性激活，然后再进行分布归一化操作。

以上是在训练过程中的流程，那么在测试阶段，我们可以只使用一个数据进行测试(无法计算均值和标准差），并且没有训练时的参数γ和β，怎么办呢？

我们需要保存并使用训练过程中的结果，来辅助运算。假设我们有30个样本，每5个样本构成一个batch进行训练，完整遍历一次训练集就要6个batch，对第一层神经网络来说，我们会得到6个均值:

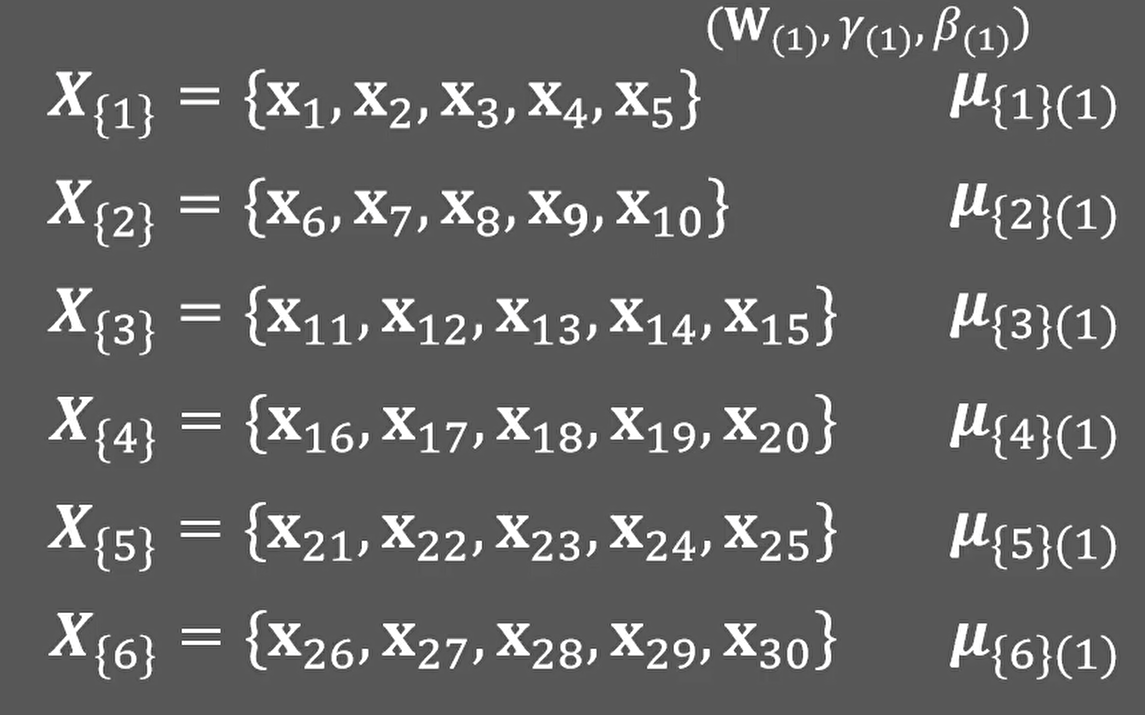
然后通过指数加权的方式求出这6个均值的平均值:

上面的m可以看做对历史的保留，类似之前讲的动量的概念。在torch框架中也将这个参数命名为momentum。默认值0.1：

总结：

• 优点
  • Batch Normalization 批量归一化方法可以加速神经网络的收敛。使训练过程中对学习率和参数初始化更加鲁棒。
• 缺点
  • 仅在Batch中包含样本数量较多时有效。因此对循环网络(RNN)或序列数据(Sequence)(如：自然语言)性能较差。
  • 由于在测试阶段需要使用训练阶段的历史数值，因此在分布式运算时额外的数据同步会影响并行效率。

为了应对BN的缺陷，后面有诞生了（了解）：

• Layer Normalization:在每一个样本特征空间内的归一化。
• Instance Normalization:在每一个样本特征空间内逐通道的归一化。
• Group Normalization:LN和IN的结合版本。

 

 

BN层是针对单个神经元进行，利用网络训练时一个mini-batch 的数据来计算该神经元x_i的均值和方差,归一化后并重构，因而称为 Batch Normalization。在每一层输入之前，将数据进行BN，然后再送入后续网络中进行学习:

首先我们对某一批次的数据的神经元的输出进行标准化：  

      

                              

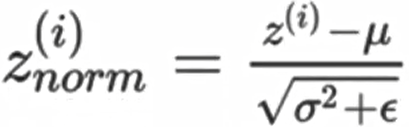
然后在使用变换重构，引入了可学习参数γ、β，如果各隐藏层的输入均值在靠近0的区域，即处于激活函数的线性区域，不利于训练非线性神经网络，从而得到效果较差的模型。因此，需要用γ和β 对标准化后的结果做进一步处理:

 

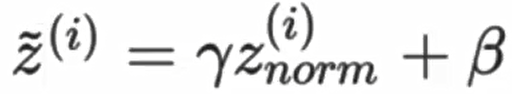
这就是BN层最后的结果。整体流程如下图所示

在tf.keras中实现使用:

tf.keras.layers.BatchNormalization(epsilon=0.001,center=True,scale=True,beta_initializer='zeros',gamma_initializer='ones')

参数	意义
epsilon	防止分母为 0
center	如果为 True，则将的偏移 beta 量添加到标准化张量。如果为 False，则将 beta 被忽略。
scale	如果为 True，则乘以 gamma。如果为 False，gamma 则不使用。
beta_initializer	Beta 权重的初始化程序。
gamma_initializer	伽玛权重的初始化程序。