10.正则化

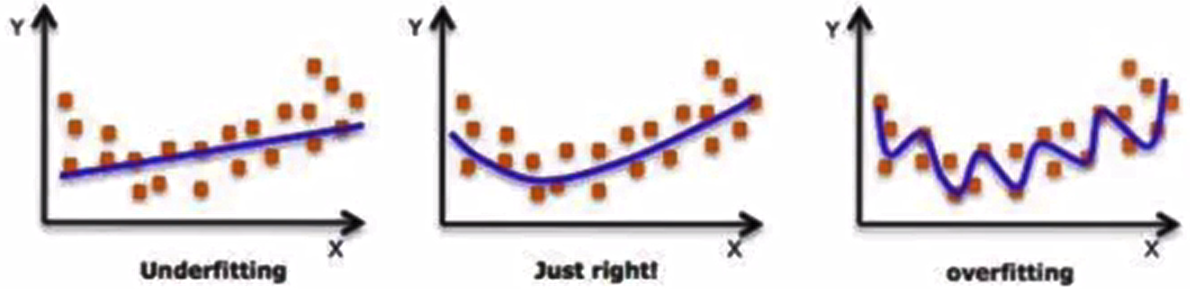
在设计机器学习算法时不仅要求在训练集上误差小，而且希望在新样本上的泛化能力强。许多机器学习算法都采用相关的策略来减小测试误差，这些策略被统称为正则化。因为神经网络的强大的表示能力经常遇到过拟合，所以需要使用不同形式的正则化策略。

正则化通过对算法的修改来减少泛化误差，目前在深度学习中使用较多的策略有参数范数惩罚，提前终止，DropOut等，接下来我们对其进行详细的介绍。

L1与L2正则化(回顾)

L1和L2是最常见的正则化方法。它们在损失函数(costfunction)中增加一个正则项，由于添加了这个正则化项，权重矩阵的值减小，因为它假定具有更小权重矩阵的神经网络导致更简单的模型。因此，它也会在一定程度上减少过拟合。然而，这个正则化项在L1和L2中是不同的。

• L2正则化

这里的λ是正则化参数，它是一个需要优化的超参数。L2正则化又称为权重衰减，因为其导致权重趋向于0(但不全是0)

• L1正则化

这里，我们惩罚权重矩阵的绝对值。其中，入为正则化参数，是超参数，不同于L2，权重值可能被减少到0。因此，L1对于压缩模型很有用。其它情况下，一般选择优先选择L2正则化。
在tf.keras中实现使用的方法是:

L1正则化

tf.keras.regularizers.L1(l1=0.0)

L2正则化

tf.keras.regularizers.L2(l2=0.0)

L1L2正则化

tf.keras.regularizers.L1L2(l1=0.0,l2=0.0)

我们直接在某一层的layers中指明正则化类型和超参数即可:

# 导入对应工具包
import tensorflow as tf
from tensorflow.keras import regularizers

# 创建模型
model=tf.keras.models.Sequential()
model.add(tf.keras.layers.Input(shape=(3,1)))
# L2正则化，lambda=0.01
model.add(tf.keras.layers.Dense(16,kernel_regularizer=regularizers.l2(0.01),activation='relu'))
# L1正则化，lambda=0.01
model.add(tf.keras.layers.Dense(16,kernel_regularizer=regularizers.l1(0.01),activation='relu'))
# L1L2正则化，lambda=0.01
model.add(tf.keras.layers.Dense(16,kernel_regularizer=regularizers.l1_l2(0.01),activation='relu'))
model.summary()

Dropout正则化(深度学习常用)

dropout是在深度学习领域最常用的正则化技术。Dropout的原理很简单:假设我们的神经网络结构如下所示，在每个迭代过程中，随机选择某些节点，并且删除前向和后向连接。 

 

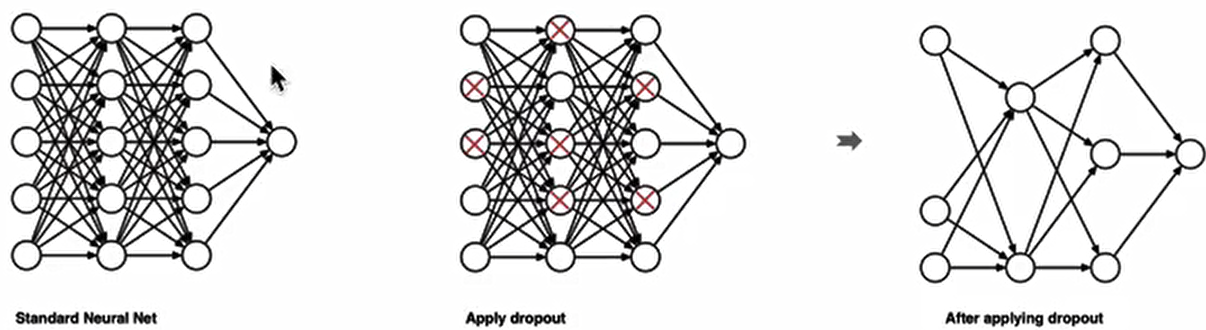
因此，每个迭代过程都会有不同的节点组合，从而导致不同的输出，这可以看成机器学习中的集成方法(ensemble technique)。集成模型一般优于单一模型，因为它们可以捕获更多的随机性。相似地，dropout使得神经网络模型优于正常的模型。

在tf.keras中实现使用的方法是dropout:

tf.keras.layers.Dropout(rate)

参数:

每一个神经元被丢弃的概率rate:

例子

# 定义dropout层，每个神经元有0.2的概率失活，未失活的神经元按照1/(1-rate)放大
layer=tf.keras.layers.Dropout(rate=0.2)
# 定义五个批次的数据
data=np.arange(1,11).reshape(5,2).astype(np.float32)
#打印原始data
print('原始data:\n',data)
# 进行随机失活，在training模式中，返回应用dropout后的输出；或者在非training模式中，正常返回输出（输出原数据）。
output=layer(data,training=True)
# 打印失活后的结果
print('失活后的结果:\n',output)

原始data:
 [[ 1.  2.]
 [ 3.  4.]
 [ 5.  6.]
 [ 7.  8.]
 [ 9. 10.]]
失活后的结果:
 tf.Tensor(
[[ 1.25  2.5 ]
 [ 3.75  5.  ]
 [ 6.25  7.5 ]
 [ 8.75 10.  ]
 [ 0.   12.5 ]], shape=(5, 2), dtype=float32)