朴素⻉叶斯

概率基础复习

概率定义

概率定义为⼀件事情发⽣的可能性

扔出⼀个硬币，结果头像朝上

P(X) : 取值在[0, 1]

联合概率、条件概率与相互独⽴

• 联合概率：包含多个条件，且所有条件同时成⽴的概率
  • 记作：P(A,B)
• 条件概率：就是事件A在另外⼀个事件B已经发⽣条件下的发⽣概率
  • 记作：P(A|B)
• 相互独⽴：如果P(A, B) = P(A)P(B)，则称事件A与事件B相互独⽴。

案例：判断⼥神对你的喜欢情况

我们通过⼀个例⼦，来计算⼀些结果：

样本数	职业	体型	女神是否喜欢
1	程序员	超重	不喜欢
2	产品	匀称	喜欢
3	程序员	匀称	喜欢
4	程序员	超重	喜欢
5	美工	匀称	不喜欢
6	美工	超重	不喜欢
7	产品	匀称	喜欢

问题如下：

1. ⼥神喜欢的概率？
2. 职业是程序员并且体型匀称的概率？
3. 在⼥神喜欢的条件下，职业是程序员的概率？
4. 在⼥神喜欢的条件下，职业是程序员、体重超重的概率？

计算结果为：

1. P(喜欢) = 4/7
2. P(程序员, 匀称) = 1/7(联合概率)
3. P(程序员|喜欢) = 2/4 = 1/2(条件概率)
4. P(程序员, 超重|喜欢) = 1/4（联合条件概率）

拉普拉斯平滑系数

思考题：上面的数据，在⼩明是产品经理并且体重超重的情况下，如何计算⼩明被⼥神喜欢的概率？

即P(喜欢|产品, 超重) = ？

我们观察上述式子发现，职业是产品，并且体型超重的数据是0条，如果直接计算该条件下被女神喜欢的概率，也等于0，这很明显不符合现实情况，造成这一情况的原因，是样本数量不足，覆盖不够广泛。

本来现实⽣活中，肯定是存在职业是产品经理并且体重超重的⼈的，P(产品, 超重)不可能为0；

⽽且事件“职业是产品经理”和事件“体重超重”通常被认为是相互独⽴的事件【即：P(产品, 超重) = P(产品)P(超重)】，但是，根据我们有限的7个样本计算 ，“P(产品, 超重) = P(产品)P(超重)”不成⽴。所以一定是样本有问题。

那么如下计算这种情况下的事件概率呢？

此时我们需要⽤到拉普拉斯平滑系数进⾏求解。

例：⽂章分类计算

需求：通过前四个训练样本（⽂章），判断第五篇⽂章，是否属于China类

	文档 ID	文档中的词	属于 c=China 类
训 练 集	1	Chinese Beijing Chinese	Yes
	2	Chinese Chinese Shanghai	Yes
	3	Chinese Macao	Yes
	4	Tokyo Japan Chinese	No
测试集	5	Chinese Chinese Chinese Tokyo Japan	?

假设：

• P(F1,F2,…)是 预测⽂档中每个词的概率
• P(C)：每个⽂档类别的概率(某⽂档类别数／总⽂档数量)
• P(W│C)：给定类别下特征的情况下，某个词出现的概率
  • 计算⽅法：P(F1│C)=Ni/N （在训练集中计算）
    • Ni为该F1词在C类别所有⽂档中出现的次数
    • N为所属类别C下的⽂档所有词出现的次数和

# ⾸先计算属于 c=China 类的情况下，Chinese、Tokyo、Japan出现的概率:

• P(Chinese|C) = 5/8(一共八个词，Chinese出现了5次)
• P(Tokyo|C) = 0/8
• P(Japan|C) = 0/8

# 接着计算不属于 c=China 类的情况下，Chinese、Tokyo、Japan出现的概率:

• P(Chinese|C) = 1/3
• P(Tokyo|C) = 1/3
• P(Japan|C) = 1/3

问题:从上面的例子我们得到P(Tokyg|c)和P(Japan|c)都为0，这是不合理的，如果词频列表里面有很多出现次数都为0，很可能计算结果都为零。

解决方法:拉普拉斯平滑系数

a为指定的系数一般为1，m为训练文档中统计出的特征词总个数

通过拉普拉斯系数重新计算概率：

# ⾸先计算属于 c=China 类的情况下，Chinese、Tokyo、Japan出现的概率:

• P(Chinese|C) = 5/8 --> 6/14（a=1,m=6(训练集一共6种词)）
• P(Tokyo|C) = 0/8 --> 1/14
• P(Japan|C) = 0/8 --> 1/14

# 接着计算不属于 c=China 类的情况下，Chinese、Tokyo、Japan出现的概率:

• P(Chinese|C) = 1/3 -->2/9（a=1,m=6(训练集一共6种词)）
• P(Tokyo|C) = 1/3 --> 2/9
• P(Japan|C) = 1/3 --> 2/9

贝叶斯

贝叶斯公式介绍

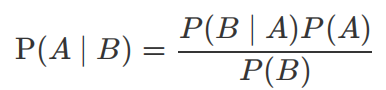
朴素贝叶斯

朴素⻉叶斯，简单理解，就是假定了特征与特征之间相互独⽴的⻉叶斯公式。

也就是说，朴素⻉叶斯，之所以朴素，就在于假定了特征与特征相互独⽴。

案例理解：

那么这个公式如果应⽤在⽂章分类的场景当中，我们可以这样看：

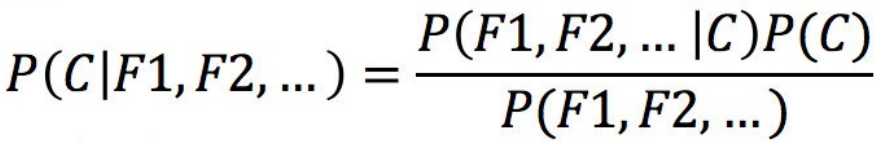
P(C)：每个⽂档类别的概率(某⽂档类别数／总⽂档数量)

P(F1,F2,…) 预测⽂档中每个词的概率

所以P(C|F1,F2,…)就是，在已知词F1,F2...出现的概率的情况下，文章分类为C的概率 ，也就是我们的目标：分类预测

案例：商品评价——好评差评判断

api介绍

• sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
  • 朴素⻉叶斯分类
  • alpha：拉普拉斯平滑系数

步骤分析

• 1）获取数据
• 2）数据基本处理
  • 2.1） 取出内容列，对数据进⾏分析
  • 2.2） 判定评判标准
  • 2.3） 选择停⽤词
  • 2.4） 把内容处理，转化成标准格式
  • 2.5） 统计词的个数
  • 2.6）准备训练集和测试集
• 3）模型训练
• 4）模型评估

# 1）获取数据
data=pd.read_csv(r"D:\learn\000人工智能数据大全\黑马数据\机器学习\朴素贝叶斯\书籍评价.csv",encoding='GBK')
data

	Unnamed: 0	内容	评价
0	0	从编程小白的角度看，入门极佳。	好评
1	1	很好的入门书，简洁全面，适合小白。	好评
2	2	讲解全面，许多小细节都有顾及，三个小项目受益匪浅。	好评
3	3	前半部分讲概念深入浅出，要言不烦，很赞	好评
4	4	看了一遍还是不会写，有个概念而已	差评
5	5	中规中矩的教科书，零基础的看了依旧看不懂	差评
6	6	内容太浅显，个人认为不适合有其它语言编程基础的人	差评
7	7	破书一本	差评
8	8	适合完完全全的小白读，有其他语言经验的可以去看别的书	差评
9	9	基础知识写的挺好的！	好评
10	10	太基础	差评
11	11	略_嗦。。适合完全没有编程经验的小白	差评
12	12	真的真的不建议买	差评

# 2）数据基本处理
# 2.1） 判定评判标准：将评价结果转换为数值:1好评;0差评
print(data['评价'].value_counts())#查看所有评价类型:差评8,好评5
data.loc[data['评价']=='好评','评论标号']=1# 把好评修改为1
data.loc[data['评价']=='差评','评论标号']=0
# data.loc[data.loc[:, '评价'] == "好评", "评论标号"] = 1 
# data.loc[data.loc[:, '评价'] == '差评', '评论标号'] = 0
data
# 2.2） 取出内容列
content=data['内容']
# 2.3） 把内容处理，转化成标准格式
# 切词
content_list=[]
for tem in content:
    # print(tem)#从编程小白的角度看，入门极佳。
        # cut_all 参数默认为 False,所有使⽤ cut ⽅法时默认为精确模式
    content_cut=jieba.cut(tem,cut_all=False)
    # print(content_cut)#<generator object Tokenizer.cut at 0x0000016E20598040>
    # print(','.join(content_cut))# ,从,编程,小白,的,角度看,，,入门,极佳
    content_list.append(','.join(content_cut))
content_list

# 2.4） 选择停⽤词
stopwords=[]
with open(file=r"D:\learn\000人工智能数据大全\黑马数据\机器学习\朴素贝叶斯\stopwords.txt",encoding='UTF-8') as f:
    lines=f.readlines()
    for line in lines:
        stopwords.append(line.strip())
# 使用set去重
stopwords=list(set(stopwords))
# 2.5） 统计词的个数
# 实例化对象
# CountVectorizer 类会将⽂本中的词语转换为词频矩阵
transformer=CountVectorizer(stop_words=stopwords)
# 它通过 fit_transform 函数计算各个词语出现的次数
X=transformer.fit_transform(content_list) # 通过 get_feature_names()可获取词袋中所有⽂本的关键字
print(transformer.get_feature_names_out()) # 通过 toarray()可看到词频矩阵的结果
print(X.toarray())
# # 2.6）准备训练集和测试集
# 准备训练集 这⾥将⽂本前10⾏当做训练集 后3⾏当做测试集
x_train=X[:10]
y_train=data['评论标号'][:10]

x_test=X[10:13]
y_test=data['评论标号'][10:13]
# 3）模型训练
estimator=MultinomialNB(alpha=1)
estimator.fit(x_train,y_train)
# 4）模型评估
pre=estimator.predict(x_test)
#预测值与真实值展示
print('预测值：',pre)# [0. 0. 0.]
print('真实值：',y_test)# 0.0   0.0    0.0
score=estimator.score(x_test,y_test)
print('模型得分：',score)#模型得分： 1.0

朴素贝叶斯算法总结

1.朴素⻉叶斯优缺点

• 优点：
  • 朴素⻉叶斯模型发源于古典数学理论，有稳定的分类效率
  • 对缺失数据不太敏感，算法也⽐较简单，常⽤于⽂本分类
  • 分类准确度⾼，速度快
• 缺点：
  • 由于使⽤了样本属性独⽴性的假设，所以如果特征属性有关联时其效果不好
  • 需要计算先验概率，⽽先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳；

2.朴素贝叶斯内容汇总

2.1 NB的原理

朴素⻉叶斯法是基于⻉叶斯定理与特征条件独⽴假设的分类⽅法。

• 对于给定的待分类项x，通过学习到的模型计算后验概率分布，
• 即：在此项出现的条件下各个⽬标类别出现的概率，将后验概率最⼤的类作为x所属的类别。

2.2 朴素⻉叶斯朴素在哪⾥？

在计算条件概率分布P(X=x∣Y=c_k)时，NB引⼊了⼀个很强的条件独⽴假设，即，当Y确定时，X的各个特征分量取值之间相互独⽴。

2.3 为什么引⼊条件独⽴性假设？

为了避免⻉叶斯定理求解时⾯临的组合爆炸、样本稀疏问题。

假设条件概率分为

2.4 在估计条件概率P(X∣Y)时出现概率为0的情况怎么办？

解决这⼀问题的⽅法是采⽤拉普怕死平滑系数处理。

简单来说，引⼊λ，

• 当λ=0时，就是普通的极⼤似然估计；
• 当λ=1时称为拉普拉斯平滑。

2.5 为什么属性独⽴性假设在实际情况中很难成⽴，但朴素⻉叶斯仍能取得较好的效果?

• ⼈们在使⽤分类器之前，⾸先做的第⼀步（也是最重要的⼀步）往往是特征选择，这个过程的⽬的就是为了排除特征之间的共线性、选择相对较为独⽴的特征；
• 对于分类任务来说，只要各类别的条件概率排序正确，⽆需精准概率值就可以得出正确分类；
• 如果属性间依赖对所有类别影响相同，或依赖关系的影响能相互抵消，则属性条件独⽴性假设在降低计算复杂度的同时不会对性能产⽣负⾯影响。

2.6 朴素贝叶斯与LR的区别？

1）简单来说：

• 区别⼀：
  • 朴素⻉叶斯是⽣成模型，
    • 根据已有样本进⾏⻉叶斯估计学习出先验概率P(Y)和条件概率P(X|Y)，
    • 进⽽求出联合分布概率P(XY),
    • 最后利⽤⻉叶斯定理求解P(Y|X)，
  • ⽽LR是判别模型，
    • 根据极⼤化对数似然函数直接求出条件概率P(Y|X)；

从概率框架的⻆度来理解机器学习；主要有两种策略：

第⼀种：给定 x， 可通过直接建模 P(c |x) 来预测 c，这样得到的是"判别式模型" (discriminativemodels)；

第⼆种：也可先对联合概率分布 P(x,c) 建模，然后再由此获得 P(c |x)， 这样得到的是"⽣成式模型"(generative models) ;

显然，前⾯介绍的逻辑回归、决策树、都可归⼊判别式模型的范畴，还有后⾯学到的BP神经⽹络、⽀持向量机等；

• 区别⼆：
  • 朴素⻉叶斯是基于很强的条件独⽴假设（在已知分类Y的条件下，各个特征变量取值是相互独⽴的），
  • ⽽LR则对此没有要求；
• 区别三：
  • 朴素⻉叶斯适⽤于数据集少的情景，
  • ⽽LR适⽤于⼤规模数据集。

2）进⼀步说明：

前者是⽣成式模型，后者是判别式模型，⼆者的区别就是⽣成式模型与判别式模型的区别。

• ⾸先，Navie Bayes通过已知样本求得先验概率P(Y), 及条件概率P(X|Y), 对于给定的实例，计算联合概率，进⽽求出后验概率。也就是说，它尝试去找到底这个数据是怎么⽣成的（产⽣的），然后再进⾏分类。哪个类别最有可能产⽣这个信号，就属于那个类别。
  • 优点： 样本容量增加时，收敛更快；隐变量存在时也可适⽤。
  • 缺点：时间⻓；需要样本多；浪费计算资源
• 相⽐之下，Logistic回归不关⼼样本中类别的⽐例及类别下出现特征的概率，它直接给出预测模型的式⼦。设每个特征都有⼀个权重，训练样本数据更新权重w，得出最终表达式。
  • 优点：
    • 直接预测往往准确率更⾼；
    • 简化问题；
    • 可以反应数据的分布情况，类别的差异特征；
    • 适⽤于较多类别的识别。
  • 缺点
    • 收敛慢；
    • 不适⽤于有隐变量的情况。