特征降维
降维
1.1 定义
降维是指在某些限定条件下,降低随机变量(特征)个数,得到⼀组“不相关”主变量的过程
- 降低随机变量的个数
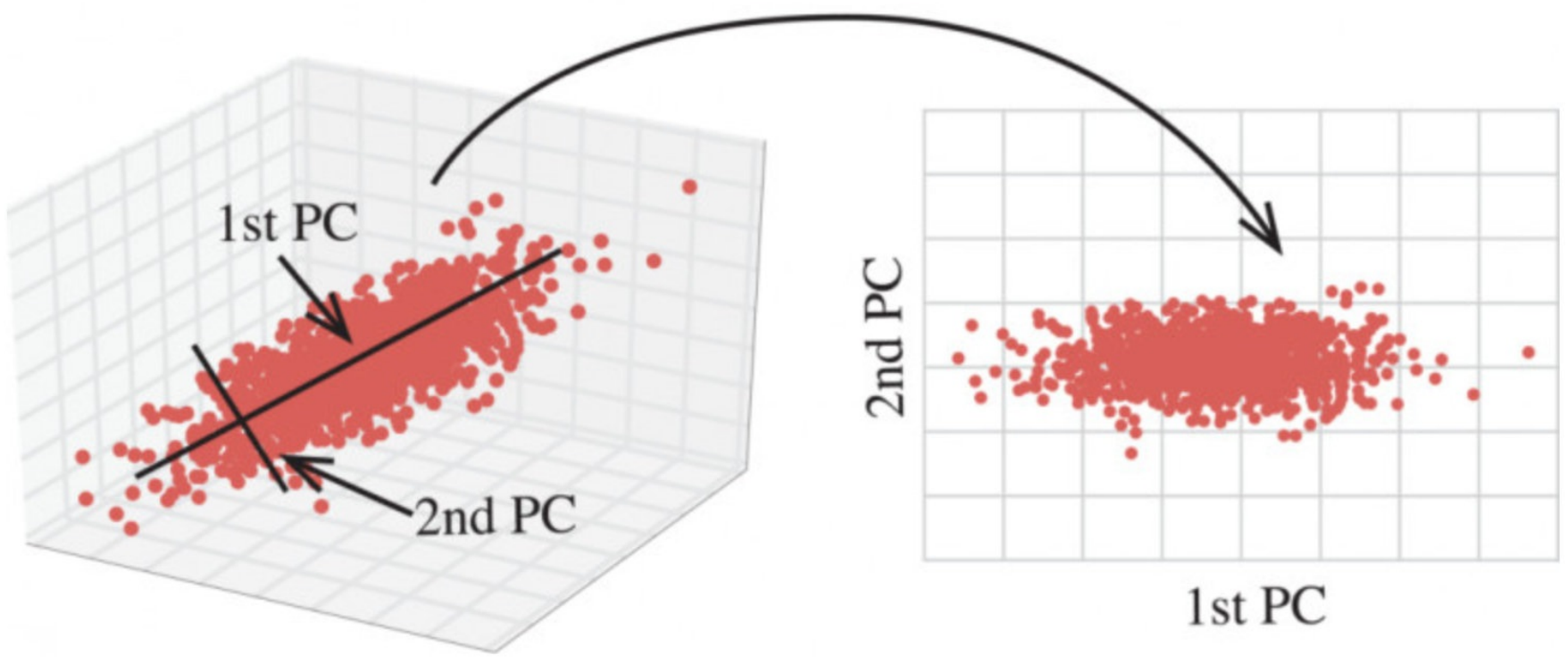
相关特征(correlated feature)
- 相对湿度与降⾬量之间的相关
- 等等
正是因为在进⾏训练的时候,我们都是使⽤特征进⾏学习。如果特征本身存在问题或者特征之间相关性较强,对于算法学习预测会影响较⼤
1.2 降维的两种⽅式
- 特征选择
- 主成分分析PCA(可以理解⼀种特征提取的⽅式)
特征选择
2.1 定义
数据中包含冗余或⽆关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征。

2.2 方法
Filter(过滤式):主要探究特征本身特点、特征与特征和⽬标值之间关联
- 方差选择法:低方差特征过滤
- 相关系数
Embedded (嵌⼊式):算法⾃动选择特征(特征与⽬标值之间的关联)
- 决策树:信息熵、信息增益
- 正则化:L1、L2
- 深度学习:卷积等
低方差特征过滤
删除低⽅差的⼀些特征,前⾯讲过⽅差的意义。再结合⽅差的⼤⼩来考虑这个⽅式的⻆度。
- 特征⽅差⼩:某个特征⼤多样本的值⽐较相近
- 特征⽅差⼤:某个特征很多样本的值都有差别
2.3.1 API
sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
- 删除所有低⽅差特征
- Variance.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:方差低于threshold的特征将被删除。默认值是保留所有⾮零⽅差特征,即删除所有样本中具有相同值的特征。
2.3.2 示例股票数据
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
data=pd.read_csv(r"D:\learn\000人工智能数据大全\黑马数据\机器学习\factor_returns.csv")
data.head()| index | pe_ratio | pb_ratio | market_cap | return_on_asset_net_profit | du_return_on_equity | ev | earnings_per_share | revenue | total_expense | date | return | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 000001.XSHE | 5.9572 | 1.1818 | 8.525255e+10 | 0.8008 | 14.9403 | 1.211445e+12 | 2.010 | 2.070140e+10 | 1.088254e+10 | 2012-01-31 | 0.027657 |
| 1 | 000002.XSHE | 7.0289 | 1.5880 | 8.411336e+10 | 1.6463 | 7.8656 | 3.002521e+11 | 0.326 | 2.930837e+10 | 2.378348e+10 | 2012-01-31 | 0.082352 |
| 2 | 000008.XSHE | -262.7461 | 7.0003 | 5.170455e+08 | -0.5678 | -0.5943 | 7.705178e+08 | -0.006 | 1.167983e+07 | 1.203008e+07 | 2012-01-31 | 0.099789 |
| 3 | 000060.XSHE | 16.4760 | 3.7146 | 1.968046e+10 | 5.6036 | 14.6170 | 2.800916e+10 | 0.350 | 9.189387e+09 | 7.935543e+09 | 2012-01-31 | 0.121595 |
| 4 | 000069.XSHE | 12.5878 | 2.5616 | 4.172721e+10 | 2.8729 | 10.9097 | 8.124738e+10 | 0.271 | 8.951453e+09 | 7.091398e+09 | 2012-01-31 | -0.002681 |
我们对某些股票的指标特征之间进⾏⼀个筛选,除去'index,'date','return'列不考虑(这些类型不匹配,也不是所需要指标)
# 先排除无关特征
useful_data=data.iloc[:,1:10]
print(useful_data.shape)#(2318, 9)
useful_data.head()| pe_ratio | pb_ratio | market_cap | return_on_asset_net_profit | du_return_on_equity | ev | earnings_per_share | revenue | total_expense | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5.9572 | 1.1818 | 8.525255e+10 | 0.8008 | 14.9403 | 1.211445e+12 | 2.010 | 2.070140e+10 | 1.088254e+10 |
| 1 | 7.0289 | 1.5880 | 8.411336e+10 | 1.6463 | 7.8656 | 3.002521e+11 | 0.326 | 2.930837e+10 | 2.378348e+10 |
| 2 | -262.7461 | 7.0003 | 5.170455e+08 | -0.5678 | -0.5943 | 7.705178e+08 | -0.006 | 1.167983e+07 | 1.203008e+07 |
| 3 | 16.4760 | 3.7146 | 1.968046e+10 | 5.6036 | 14.6170 | 2.800916e+10 | 0.350 | 9.189387e+09 | 7.935543e+09 |
| 4 | 12.5878 | 2.5616 | 4.172721e+10 | 2.8729 | 10.9097 | 8.124738e+10 | 0.271 | 8.951453e+09 | 7.091398e+09 |
#低方差特征过滤
flter=VarianceThreshold(threshold=1)
flter_data=flter.fit_transform(useful_data)
flter_data.shape#(2318, 8)#低方差特征过滤-增大阈值
flter=VarianceThreshold(threshold=10)#方差要求更大,过滤掉更多数据
flter_data=flter.fit_transform(useful_data)
flter_data.shape#(2318, 7)相关系数
主要实现⽅式:
- ⽪尔逊相关系数
- 斯⽪尔曼相关系数
皮尔逊相关系数(Pearson Correlation Coefficient)
1.作⽤
反映变量之间相关关系密切程度的统计指标
2.公式计算案例(了解,不⽤记忆)
公式
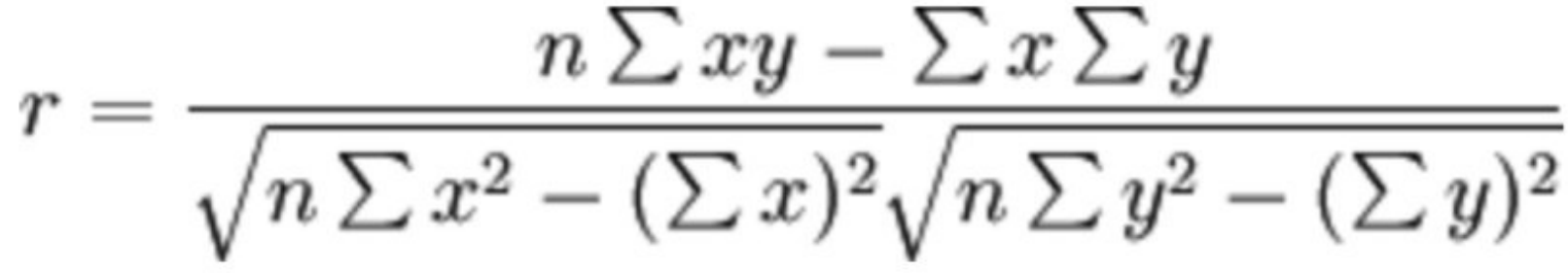
举例
- ⽐如说我们计算年⼴告费投⼊与⽉均销售额
广告费与月平均销售额的相关数据表 单位:万元

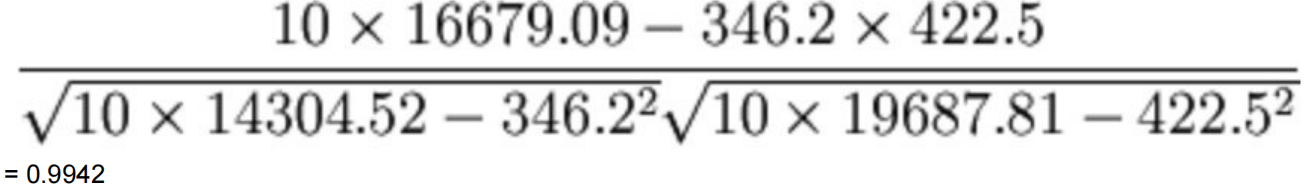



 浙公网安备 33010602011771号
浙公网安备 33010602011771号